CS558a Syllabus & Progress

Pyramid Broadcast Technique for Video on Demand

Reading material
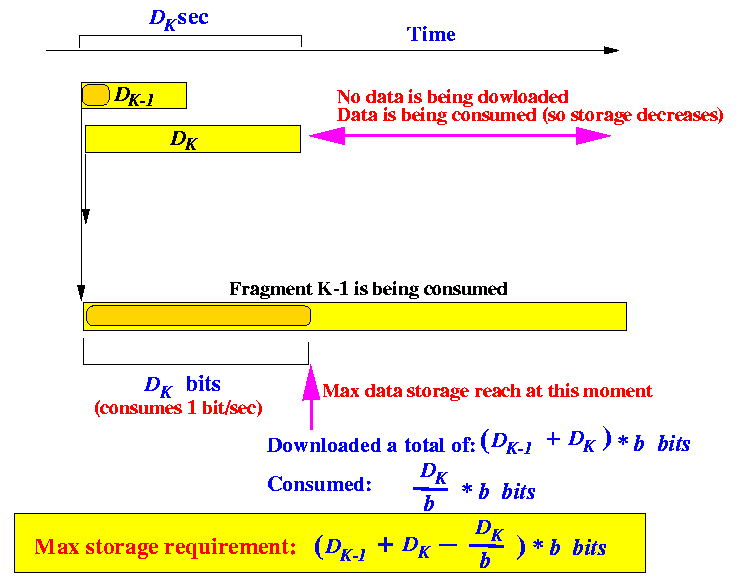
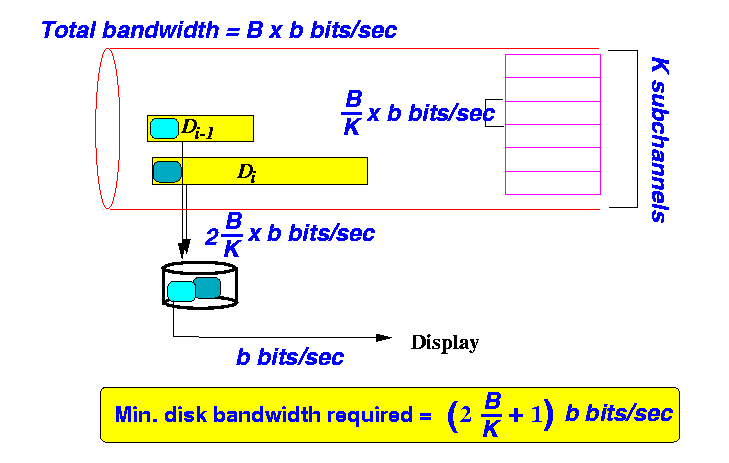
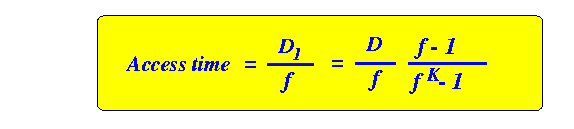- This material is not available from text books
- Reasearch paper: Pyramid Broadcasting for Video on Demand Service, click here
  - by: S. Viswanathan and T. Imielinski
  - published in: Multimedia Systems, 1996
Main Contribution of Pyramid Broadcasting
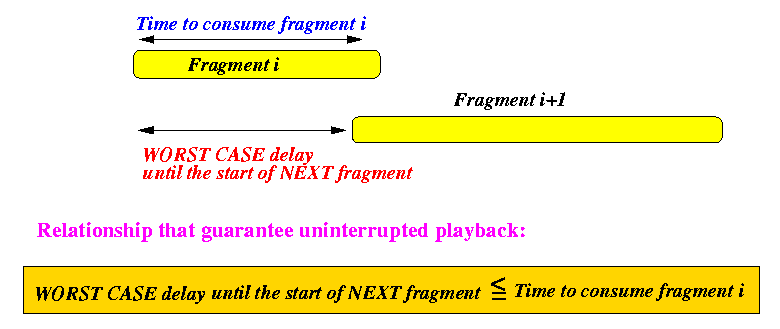
- Previously, we saw previously that Round Robin broadcasting achieves an access time of:
  - M = The number of video objects
  - D = length of each video object (all video objects have same length), normalized to the consumption rate.
  - B = The total amount bandwidth of channel, normalized to the consumption rate.
- This access time was achieved in staggered and non-staggered transmission - so staggering does not affect the access time (it does affect the amount of data that the receiver must buffer)
- The Pyramid Broadcasting technique was the first technique developed that can reduce the access time using the same system parameters
- Later techniques have been developed that improve on some shortcoming of the Pyramid Broadcasting technique, but nevertheless, Pyramid Broadcasting was the first to point this research to a whole new direction.
Parameters used in Pyramid Broadcasting
- Recall the parameters of the Video on Demand system in general:
  - M = The number of video objects
  - D = length of each video object (all video objects have same length), normalized to the consumption rate.
  - B = The total amount bandwidth of channel, normalized to the consumption rate.
- The performance of the Pyramid Broadcasting method depends very heavily on the following parameter.
- The larger the number of fragments used, the smaller the access time becomes (i.e., users will see the video sooner.
- But larger fragments will also require the receiver to use more buffer space to store the video (for delayed replay)
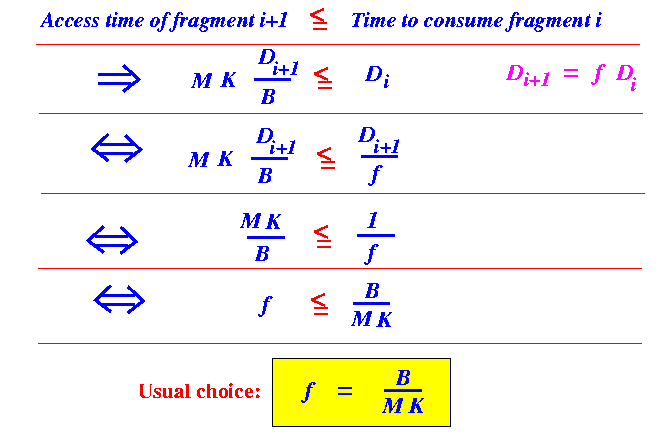
- The following parameter f is defined as a convenience to explain the Pyramid Broadcast technique.
  This parameter (f) is derived from the parameter K (number of fragments)
  The parameter f will be explained later, for now, I will just simply tell you that:
- f determines the size of the fragments used in Pyramid Broadcast
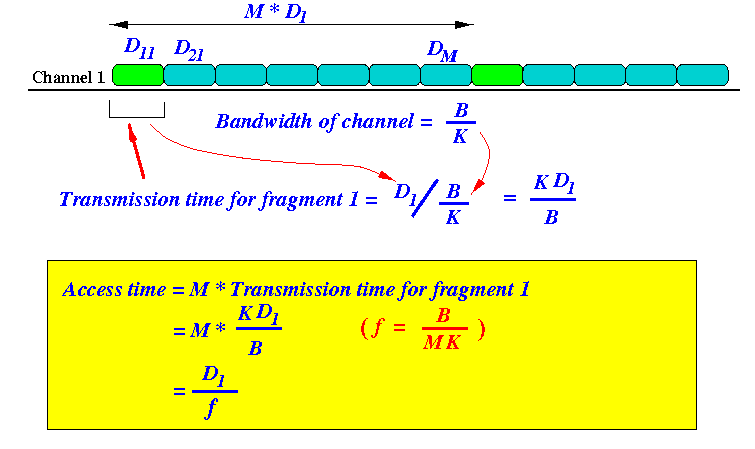
  1. As you know, each video object is partitioned into K segments - but each segment has a different size !!!
  2. In fact, video objects are partititioned into fragments of increasing size
  3. The size of fragment (i+1)^th fragment is determined as follows:
    where D_i is the size of fragment i
- Finally, we have the "natural condition" that the sum of all K fragments must be equal to the original video (you don't want to lose some video :-)):
- Example:
  Suppose:
  - Number of video objects M = 2
  - Size of each video object D = 700
  - Total bandwidth B = 12
  Suppose we select K = 3
  Then, according to the formula above, we must divide each video object into this many segments:
  The following figure shows the division of one video object into K = 3 where each subsequent segment if f = 2 times as large as the previous one:
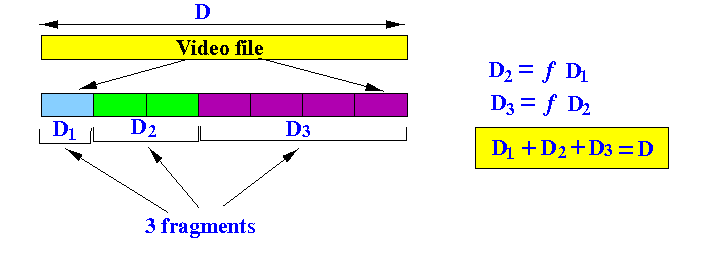
- Since:
  - D₂ = 2 * D₁
  - D₃ = 2 * D₂
  - D₁ + D₂ + D₃ = D
  We have that:
  - D₁ + 2 D₁ + 4 D₁ = D
  - Or: 7 D₁ = D = 700
  - So: D₁ = 100
  - And: D₂ = 200
  - And: D₃ = 400
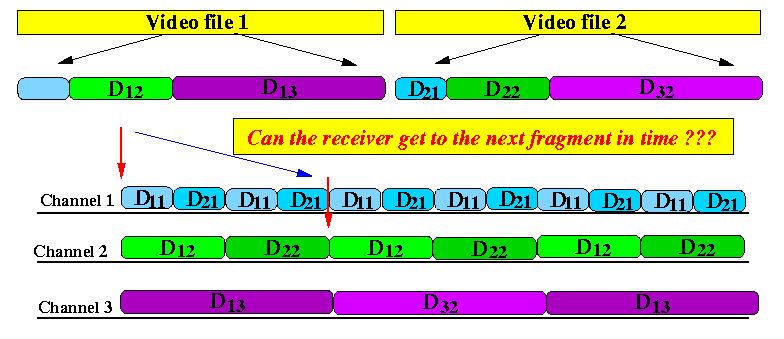
The Pyramid Broadcasting Algorithm
- The Pyramid Broadcasting method consists of:
  - Transmission algorithm used by the sender
  - Receive algorithm used by each receiver.
- Unlike the Round Robin Broadcasting method that transmits the video object in one single channel, the Pyramid Broadcasting method transmits each fragment in one single channel
  (And will therefore transmit the video object in K channels, since one video object is partitioned into K fragments)
The Transmission Algorithm in Pyramid Broadcasting
- The transmission medium is partitioned into K channels
  (Recall that K is the number of fragments.
  Pyramid Broadcasting will send one fragment in each channel)
- NOTE::
- Recall that:
  - There are M video objects
  - Each video object is partitioned into K fragments
- The fragments of the M video objects are "distributed" over a number of channels in the following manner:
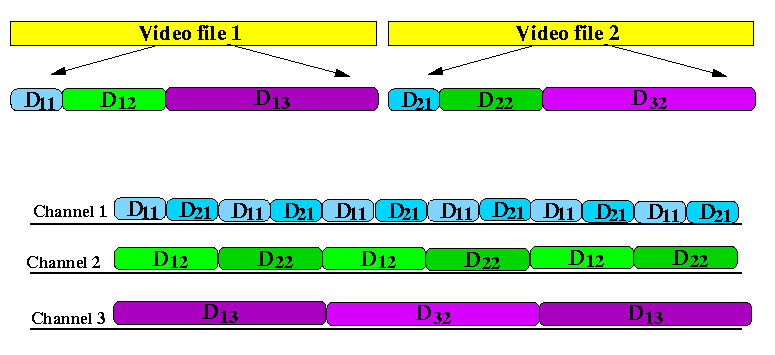
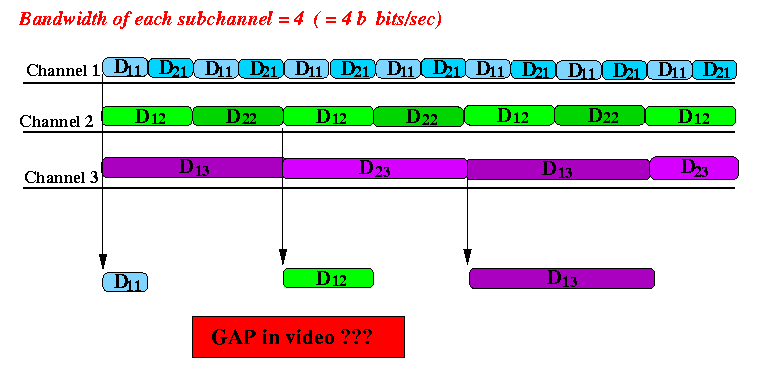
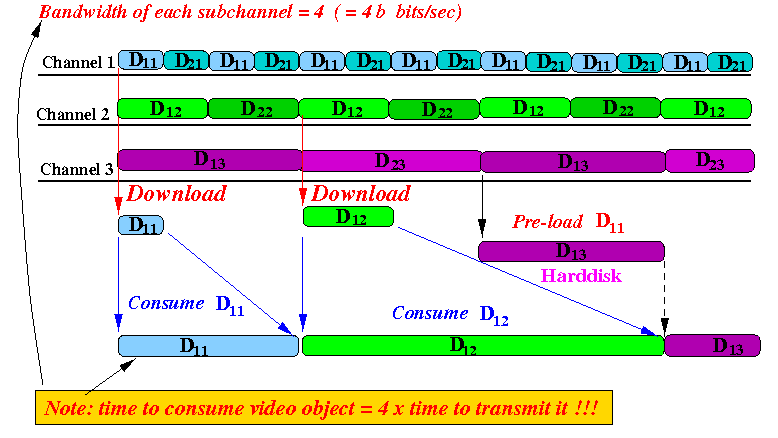
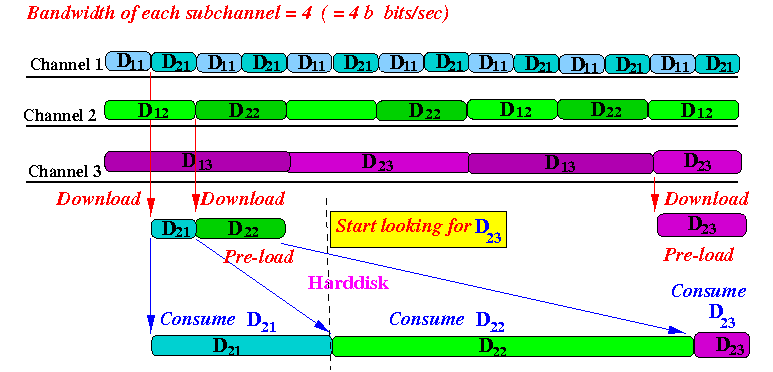
  1. Channel 1 repeatedly transmits the first fragment D₁ from all video objects, over and over again
  2. Channel 2 repeatedly transmits the second fragment D₂ from all video objects, over and over again
  3. and so on...
  4. Channel K repeatedly transmits the last fragment D_K from all video objects, over and over again

Prelude to the Receive Algorithm in Pyramid Broadcasting

OK, before I start discussing the receive algorithm, I like to point out the subtlety of this exercise:
- As you can see from the Transmission algorithm, the sender transmits the fragments of the same video object over K different channels !!!
- Obviously, we want the user to see a continuous stream of video :-)
In order for a receiver to display the video continuously, the receiver must be able to:
- Find the first segment of the video (relatively easy)
- Before the first segment of the video finishes playing, the receiver must be able to receive the second segment of the same video object (otherwise, the receiver will have broken video !)
- And so on (I.e.: before the second segment of the video finishes playing, the receiver must be able to receive the third segment of the same video object, etc., etc.)
We assume that the receiver knows the channel on which (through some information database sent from the sender and stored by each receiver)
So the problem:
is solved.
Now, if you look at the way the video objects are sent:
you will see that there can be a time gap between successive fragment transmission of fragments that belong to the same video object !!!
Example:
- A receiver for object D₁ can receive the first fragment D₁₁ at time 0 (the first fragment on Channel 1)
- The second fragment is only available after 4 D₁ fragment gaps later.
If you put 2 and 2 together, you will have to wonder:

The Receive Algorithm in Pyramid Broadcasting

Before we answer the question whether the receiver is always able to obtain the next stream before the current video fragment finishes playing, we need to know HOW video object a receiver receives the video in Pyramid Broadcasting.
I will first discuss some pre-conditions or requirements that a receiver must meet in order to implement the Pyramid Broadcasting

Pre-conditions (requirements) for Receive Algorithm of Pyramid Broadcasting

A receiver must be able to receive from 2 channels simultaneously
Some video will need to be pre-received and stored for later viewing
Therefore:

The Receive Algorithm of Pyramid Broadcasting is as follows:

A receiver will always download a video fragment starting from the beginning of the fragment.
(In other words, the receiver will never receive a fragment starting from the middle and then wait for the beginning to show up sometime later)
Receiver begins downloading the video object by:

Tuning in to Channel 1
Wait for the (first) video fragment from the desired video
Start consuming it immediately (i.e., display the video).
Fragment i+1 is downloaded only after receiver has already began downloading fragment i
In other words:

Downloads of fragment i and fragment i+1 does not begin simultaneously
After the receiver has started consuming video fragment D_i (from Channel i), it will:

Tunes to Channel i+1
When it detects the desired video D_i+1 (from the same video object) on the channel, the receiver will download (pre-receive) the fragment D_i+1 and save it to disk for later viewing.

(Note that due to step (3) of the Algorithm, the start of the download of data fragment D_i+1 can only start strictly after the receiver has started downloading fragment D_i)

Pyramid Broadcasting Examples

The transmission algorithm of Pyramid Broadcasting is pretty simple...
The best way to illustrate the receive algorithm is with examples.
System Parameters
1. Bandwidth of the whole channel B = 12 (so actual bit rate = 12 b bits/sec - video consumption rate is b bits/sec)
2. Number of video objects M = 2
3. Size of of each video object D = 700
Pyramid Broadcast Specific Parameters
1. We choose to use the number of fragments K = 3
2. This results in:
3. The increase factor f is computed as:
Pyramid Broadcast Transmission of these 2 video objects:
How a receiver that starts at time 0 downloads the different video framgment of video object 1:
Is there a PROBLEM ???
- If you look at the above figure, you will see gaps in the reception...
- Ordinarily (if the transmission rate and the consumption rate was the same), we would have gaps ("empty time") when the video is displayed...
- But there is NO gaps in the viewing of the video, when though there are gaps in the reception
- Bandwidth of the whole channel B = 12 (so actual bit rate = 12 b bits/sec - video consumption rate is b bits/sec)
- The channel is subdivided into K = 3 (sub)channels
- So each subchannels is B/K = 12/3 = 4 (actual bit rate 4 b bits/sec, or 4 times the consumption rate !)
- What this means is that:
- The following is how this receiver (that starts downloading at time 0) playout the downloaded video object fragments:
  1. Start downloading & consuming fragment 1 at time 0
    Note that it takes 4 times as long to consume the video object than transmitting it !
  2. When fragment 1 is consumed, we are just in time to download and consume fragment 2 !!!
  3. Fragment 3 becomes available while the receiver is consuming fragment 2...
    Therefore, we must pre-load fragment 3 to harddisk and consume it later.
  4. NO Gaps in viewing the video !!!
How a receiver that starts at time 0 downloads the different video framgment of video object 2:
- The following is how a receiver downloads and plays out video object 2 (continuously) if it starts downloading at time 0:
  1. Receiver waits for the start of the first fragment (D₂₁)
    Receiver start consuming the fragment at this time and will also start looking for fragment D₂₁
  2. While consuming D₂₁, receiver looks for the next fragment D₂₂ and download it
  3. Notice that a fragment D₂₃ is found before the receiver starts consuming fragment D₂₂
    This fragment D₂₃ is NOT downloaded (skipped) because the next fragment is only downloaded after consumption of the previous segment has begun.
  4. After receiver starts consuming D₂₂ it looks for the start of D₂₃ and download it if it encounters the beginning
    You see that the start of D₂₃ is downloaded before the receiver finishes displaying fragment D₂₂.

Guaranteeing non-interrupted playout in Pyramid Broadcasting

The examples above showed 2 cases where we saw that the receiver is able to display the entire video object without gaps.

We can assert that:

A receiver is able to display the entire video object without gaps if:

always be able

start downloading

D_i+1

D_i

(That is because the receiver starts looking for fragment D_i+1 when it has started consuming fragment D_i)

We can mathematically prove a relationship that will ensure that a receiver will always be able to download the next fragment while consuming the current fragment.
The following relationship gives the setting of the system parameters so that the video can be played out uninterrupted:
The figure depicts:
1. Time that the receiver takes to consume fragment D_i
2. Time when the receiver is able to start downloading fragment D_i+1
The time the receiver takes to consume fragment D_i is equal to the length of the fragment (= D_i)
The time when the receiver is able to start downloading fragment D_i+1 in the worst case is equal to the access time of fragment D_i+1.

We can calculate the access time of fragment D_i+1 as follows:

Within each channel, the fragment D_i+1 of a video object is repeatedly broadcasted - it is one among the M objects in that channel.
So the transmission scheme for D_i+1 is exactlt like "Round Robin" and we have calculated the access time for such a broadcast scheme before... (see click here ).
The worst case delay until the start of fragment D_i+1 is equal to:
D_i+1 D_i+1 M ----- = M K --- (B/K) B

NOTE: The total bandwidth available for broadcasting on that channel is B/K because the total channel bandwidth B is divided into K (sub)channels

Therefore, we must satisfy the following condition to guarantee that the receiver can display the video without gaps:
NOTE:
Reflection time.....
- So why do we go through this trouble of cutting the file in increasing sizes ?
- We saw that the "naive" way of broadcasting M video objects - each of size D - on a channel of bandwidth B resulted in an access time of: MD/B (see: click here)
- So: What is the access time of the pyramid broadcast method ?
  (Hint: it'd better be smaller than MD/B or else we have gone through all this trouble to gain nothing !!! :-))
Access time of the Pyramid Broadcasting method
- The variable D₁ is derived and we need to express D₁ of other system parameters to obtain a "proper result".
  The video object has length D (D is a proper parameter of the system)
  We know that the whole video object is devided into K objects 1, 2, ..., K where their lengths are related as:
  D_i = f * D_i-1 ......... (1)
  So:
  - D₁ = D₁
  - D₂ = f*D₁
  - D₃ = f*D₂ = f²*D₁
  - D₄ = f*D₃ = f³*D₁
  - and so on...
  - D_K = f*D_K-1 = f^K-1*D₁
  The total length of these K frgaments must be equal to the length of the original video object, so:
                 D₁ + D₂ + D₃ + ... + D_K = D
                 D₁ + f * D₁ + f² * D₁ + ... + f^K-1 * D₁ = D
                 D₁ * (1 + f + f² + f^K-1) = D ........................................... (2)
  From Calculus 101, you may still remember that
```
                         f^K - 1
     1 + f + f² + f^K-1 = -------       ...... (3)
                         f - 1
   
```
  If not, you can derive it by multiplying both sides of the equation above by f and add them up.
  Substitute equation (3) in equation (2), we get that:
```
       f^K - 1
    D₁ -------  =  D
       f - 1
   
```
  Or:
  f - 1 D₁ = D ------- ......... (4) f^K - 1
  
  Substitute equation (4) in the expression for access time above ( click here ), and we get:
  It looks like that the access time is dependent on f and K.
  However, since K = B/(M * f) (B (bandwidth) and M (# of video objects) are fixed system parameters), the access time is really only dependent on f
- Comparing access time of pyramid broadcast and round robin:
  - Access time in round robin = (M x D)/B
    Decreases linearly when bandwidth B increases
  - Access time in pyramid broadcast decreases exponentially when bandwidth B increases !!!
    (According to the formula above for the access time, the access time decreases exponentially when f increases. f increases linearly when B increases, therefore, access time decreases exponentially when B increases)
- The best (optimal) access time in pyramid broadcasting:
  - The optimal (smallest) access time can be found by minimizing the expression:
    D f - 1 Access Time = --- ------- ......... (4) f f^K - 1
  - Since D is a fixed system parameter, we can only manipulate f to find the minimum.
  - The authors has determined that the minimum is reach for f approximately equal to 2.5
  - As an exercise, you will compare the access time between the pyramid broadcasting and the round robin scheme: click here
Storage requirement in pyramid broadcasting
- The receiver is required to pre-receive some video and store it on hard disk
- A very important question to ask is:
  - How much disk space does the receiver need
- One trivial answer would be D * b bits, because the entire video object is consumed in D sec and the consumption rate is b bits per second
  The total size of the video object is D * b bits.
  If you have space to store the whole video object, you certainly have enough space :-)
- The proper question to ask is:
  - What is the minimum amount of disk space needed in pyramid broadcast
  - The answer ofcourse will depend on the size of the video object (D) and the number of fragments (K) ....
- The receiver will download at most two streams simultaneously.
  The two largest fragments are fragments K-1 and K
  So the maximum amount of data that need to be stored is when the receiver is downloading fragments K-1 and K simultaneously.
  Since fragment K-1 is downloaded first, we have this situation:
  - We know the size of fragment 1 from equation (4) ( click here )
  - We also know the size of fragment K-1 and K from equation (1) ( click here )
  - Hence:
    f - 1 D_K-1 = f^K-2 D ------- f^K - 1
    and
    f - 1 D_K = f^K-1 D ------- f^K - 1
  - I trust you can fill these into the equation above... I ain't gonna do it... the result is too messy....
Advantage of pyramid broadcasting:
- Very short access time (compared to the round robin method for the same amount of bandwidth and number of video objects)
Disadvantages of pyramid broadcasting:
- You need to save a very large portion of the video object, thus requiring a very large amount of disk storage space
  - Receiver must save the entire fragment K and most of fragment K-1.
  - These are the two largest fragments !!!
  - Just give you some idea, say we cut the video object up into 10 fragments and D_i = 2 * D_i-1. Then:
    - D₁ = D₁
    - D₂ = 2 * D₁
    - D₃ = 4 * D₁
    - D₄ = 8 * D₁
    - D₅ = 16 * D₁
    - D₆ = 32 * D₁
    - D₇ = 64 * D₁
    - D₈ = 126 * D₁
    - D₉ = 256 * D₁
    - D₁₀ = 512 * D₁
    - Total length of video object = (1 + 2 + 4 + ... + 512) * D₁ = 1023 * D₁
    - Total length of 2 largest video fragments = (256 + 512) * D₁ = 768 * D₁
    - That's more than 75% of the whole video object !!!
- High disk bandwidth:
  - Disk bandwidth is the data (read + write) access rate to the disk that is necessary to support the video playback.
  - The highest data rate needed in pyramid broadcast is when:
    - Two fragments are being downloaded simultaneous
    - Playback draws from one of the fragments on disk
  Therefore: