- One of the obvious goal of the Video on Demand system is:
Minimize the response time between (1) requesting a video and (2) starting to receive the video
- Let us consider the "obvious" (naive) solution:
- Using the traditional client/server paradigm:

- the client sends a requests for a video object
- the server (if channel is available) sends the video
- Problems with this approach:
- When
different clients
request the
same video stream
but at different times,
the requests are served by
different video stream
(because the video stream are started at different times)
- In this scenario, we
cannot use
broadcast/multicast technique
to transmit the video to different clients
when they request the
same video stream
at different times
For example, a video stream was started at 7:00 PM. Then a client that requests the same video at 7:01 PM. The new client cannot use the video from 7:00 PM, because client at 7:01 PM will miss the start of the video
(we assume that we want the client to see the video from the beginning because otherwise he would have ample reasons to complain...)
- When
different clients
request the
same video stream
but at different times,
the requests are served by
different video stream
(because the video stream are started at different times)
- Consequence of Client/Server approach:
- In the client/server approach,
we need to use
unicast forwarding
to serve individual clients:
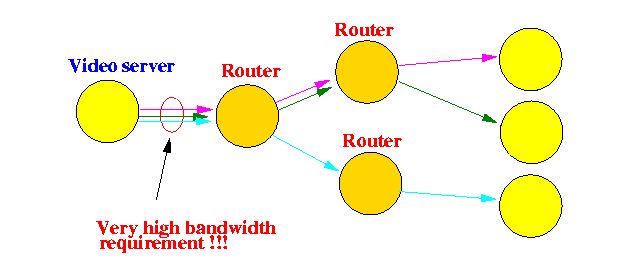
- Notice the multiplicity of video stream transmissions
from the video server in the above solution...
- Since a TV stream takes 1.5 Mbps and a HDTV video stream
requires around 15 Mbps,
(a video link can carry about 1 G bps)
we can support more than a few hundreds of customers:
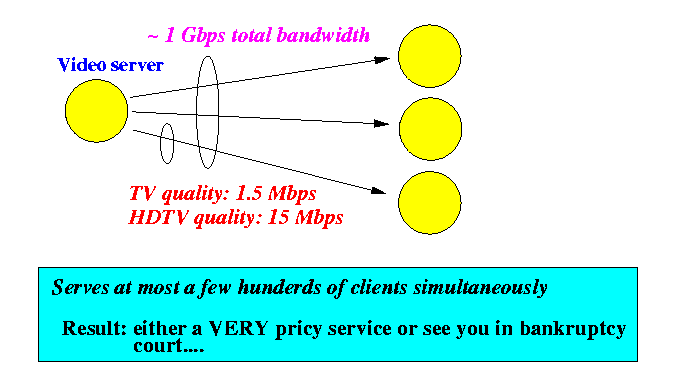
- In the client/server approach,
we need to use
unicast forwarding
to serve individual clients:
Can we do better ???
- In order support a higher number of users, we must
multicast -
we must serve more than one customor with one stream...
- We
can (are able to)
use
multicast
to distribution video "on demand"
if
we
relax
the instantaneous satisfaction requirement
and replace it with a
"quasi instantaneous" service.
:
- When the video server receives a request for a video,
we do not
start a
new broadcast immediately
- Instead, we
wait
for a period of time
(say t sec)
---
in the hope that there will be more requests
for the same video
NOTE: that would be the typical case for "hot movies" (new releases)
- All requests made in the "waiting period" (that can be as short as 10 sec to 1 min), are served by one new broadcast
- When the video server receives a request for a video,
we do not
start a
new broadcast immediately
- We must
strike a balance
between:
- efficiency
(saving bandwidth by
waiting for duplicate requests from a movie)
- responsiveness: the delay between the request and when the movie begins to show
- efficiency
(saving bandwidth by
waiting for duplicate requests from a movie)
- The longer the "waiting period", the more likely that
the video stream will serve
more than one request
But it also decrease the "responsiveness" - because we can't show the movie until the waiting period is over...
- The system will always start
a new
broadcast/multicast video stream
after every t sec of waiting.
Each video is transmitted on a different (sub)channel
- So, if a video is
extremely popular,
multiple video streams will be started at different times:

- All requests arriving between the start of stream 1 and 2
will be serviced using stream 2
- This method of transmissions is called staggered broadcast
- All requests arriving between the start of stream 1 and 2
will be serviced using stream 2
- The length of the
waiting period
before transmitting the video has a profound
affect on the number of video streams needed:
- For example, suppose the movie is 90 min long.
- If we set the maximum waiting time to 30 min (kinda long),
we would only need
3 video streams
to serve
all requests !!!
(Because the first video stream will end after 3 x 30 min - so we can "recycle" the channel used by the first video)
- To reduce the max waiting time to 1 min, we need to use 90 streams !!! (That's a lot of channels :-))
- For example, suppose the movie is 90 min long.
- Some Terminology:
- The
client/server approach
is called
user centered
because each user is allocated the same bandwidth.
- The staggered broadcast approach (using multicast) is called data centered because each data set (video stream) is allocated the same amount bandwidth.
- The
client/server approach
is called
user centered
because each user is allocated the same bandwidth.
TERMINOLOGY: Channel capacity, video transmission rate and consumption rate
- Before I proceed with the rest of the material,
I like to make the following difference clear:
- video consumption rate
- video transmission rate
-
Video consumption rate
- The
video consumption rate
is the
output data rate of the video encoder
:
- The video is captured at a certain number of frames per second (fps)
- typically 30 fps
- The video frames are then encoded (using an MPEG encoder)
- The encoder will produce a stream of output and
this output will have a certain
data rate
(typically 1.5 Mbps for low quality VHS MPEG-1 and 15 M bps
for high definition TV):
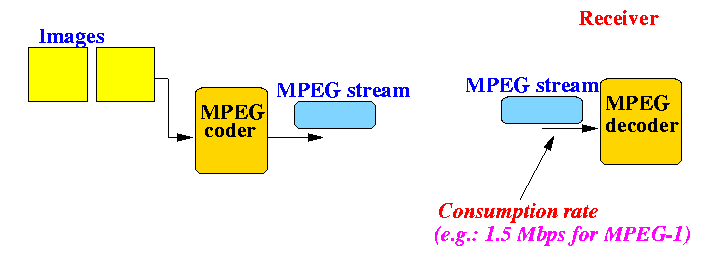
- When the video stream arrives at the receiver (user),
the video is
consumed
at the
video consumption rate
- Since we will want to watch the movie progress in the
same speed in time,
the frames are
displayed at the same rate
as when they were captured
- This will result in a video consumption rate that is equal to the output data rate of the video encoder
- The video is captured at a certain number of frames per second (fps)
- typically 30 fps
- The
video consumption rate
is the
output data rate of the video encoder
:
-
Video transmission rate
- The
video transmission rate
is the
data rate
at which the video stream is transmitted from the
sender to the receiver
- The only requirement of the
video transmission rate
is that it must be
equal to greater to
the
video consumption rate
(It CANNOT be less, because then the video will be disrupted and very hard to view (you will get lots of complains from your clients...)
- Ideally,
video transmission rate
is the same as the
video consumption rate
In this case, the receiver does not need additional memory to buffer the excessive video (it consumes the received video immediately)
- When the
video transmission rate
is greater
than the
video consumption rate,
the receiver will need to buffer the received video
(typically using a
hard disk - like TIVO)
Example:
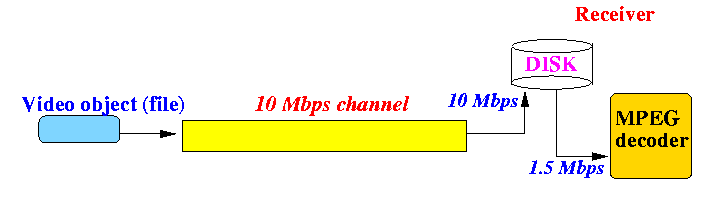
If the video transmission rate is higher than the video consumption rate, the receiver will have to buffer the excess data delivered using a disk - because the data is consumed at a lower data rate.
The buffered data can be "consumed" later.
- The
video transmission rate
is the
data rate
at which the video stream is transmitted from the
sender to the receiver
-
Access Time
- We have "heard" about this term before, here I like to
define it more rigorously.
- The
access time T
of a video object is:
- the
largest possible delay
that the client will have to wait to consume the video object
starting from the moment
that the client made the request for the object.
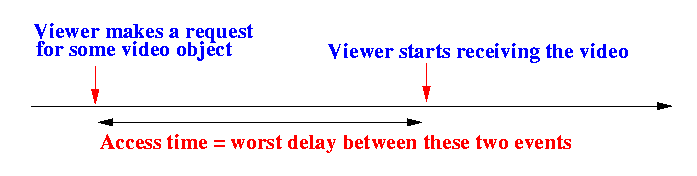
So, the access time T is the worst case scenario.
- Example:

From the figure, we can see that some users waits longer than other users after they made their request.
However, according to the above definition, the access time T for all users are the sameT !!! (which is the largest possible delay that a user has to wait to see the video)
- We have "heard" about this term before, here I like to
define it more rigorously.
-
Storage requirement
- The receiver may need to store the video
when the transmission rate exceeds the consumption
rate
- What is the maximum amount of data that need to be buffered ?
(Note: this question was important before the prices of the hard disks have fallen so dramatically. Nowadays, this question may be less relevant; nevertheless, it is interesting to study it)
- The receiver may need to store the video
when the transmission rate exceeds the consumption
rate
- We will normalize the data size by
the
data consumption rate b
- In other words:
If it takes D seconds to "consume" (view) a video object, then we say that its size is D - Since the
"consumption rate"
is b bits/sec,
the actual data size of the video object is
D * b bits
(But we will use D to denote its size in our discussion, we do not use bits as unit for the data size)
- We will also use
data consumption rate b
as the unit to measure the
channel capacity:
If the channel capacity is B * b bits/sec, then we say that the channel capacity is B. -
NOTE:
this kind of "scaling" conversion is commonly done in Physics to
get the numbers used in the computations
to the same scale (i.e., "largeness"))
- Summary
- If the channel capacity (Bandwidth) is
B
and
the size of the video object (data) is
D,
then it will take
D/B second
to send the video object to the receivers.
- If the channel capacity (Bandwidth) is
B
and
the size of the video object (data) is
D,
then it will take
D/B second
to send the video object to the receivers.
Simpleminded broadcasting: Round Robin
- We will start studying the performance of
Video on Demand system by studying
a simpleminded broadcast technique:
Round Robin
- Let's assume
- There are M video objects and
- Each video object has size D.
- Let the channel capacity be equal to
B
- The first version of
the Round Robin
transmission scheme is
non-staggered
and proceeds as follows:
- We transmit video objects one at a time and we use the complete channel capacity to transmit video objects
- Question: what is the access time ?
- Size of a video object is D
- The channel capacity is equal to
B
- So it will take
D/B seconds to transmit
one video object (to the viewers).
- There are M video objects
total.
- So, the access time can be obtained as follows:
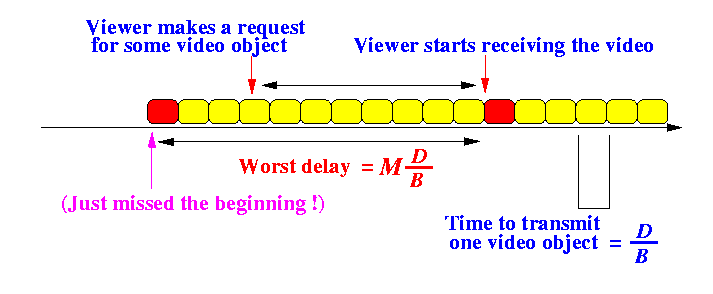
- The worst delay is when the viewer makes a request at the time just after the start of the movie...
- Size of a video object is D
- The second version of
the Round Robin
transmission scheme is
staggered
and proceeds as follows:
- We devide the whole channel (channel capacity
B)
into
B
subchannels, and each channel has
capacity of
1
So the transmission rate is equal to consumption rate - exactly as Cable TV...
- We divide the
B
channels among
the M
video objects:
-
each video object gets
B/M
channels to transmit themselves.
- We devide the whole channel (channel capacity
B)
into
B
subchannels, and each channel has
capacity of
1
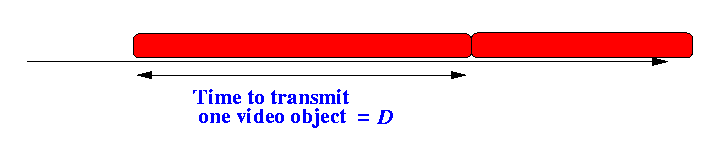
- Question: what is the access time ?
- Size of a video object is D
- Because the channel capacity is 1, it will take
D seconds
to transmit one video object to
the viewers:
- Since we have
B/M
channels to transmit the same
video object, we can
space the transmissions equally
as follows:
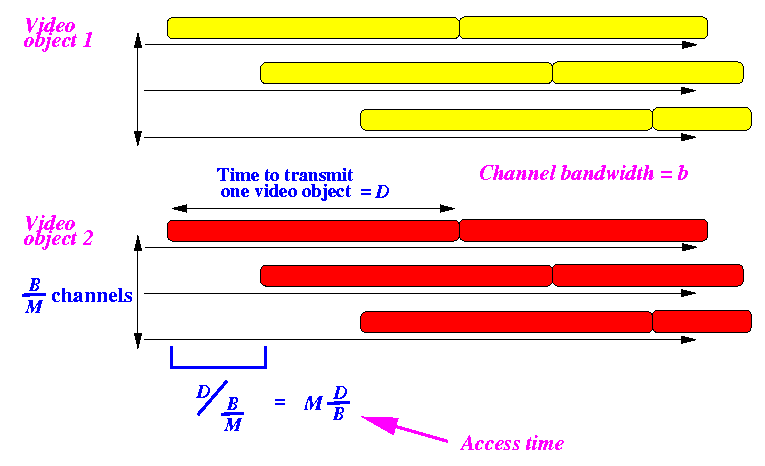
- Consequently,
the
worst delay
is experienced when the viewer makes a request
at the time
just after the start
of a video object:
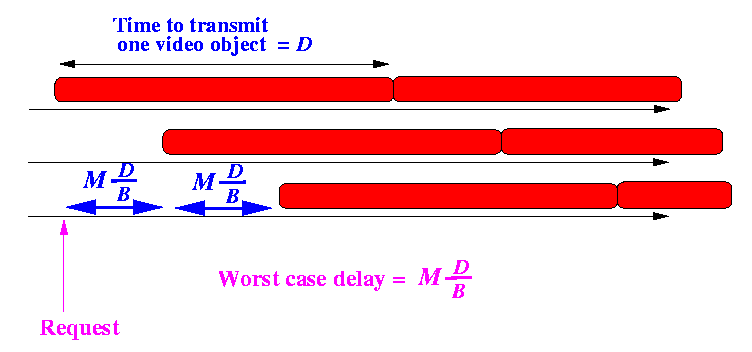
- Conclusion: access time = M*D/B
- Size of a video object is D
- Result:
-
There is no difference in access time using
Round Robin broadcast method
using staggered or non-staggered method....
- Any brilliant ideas ???...