---

Distributed Computation of ε-approximate quantiles on Data Streams

---

• Problem Description
  • Network to gather data:

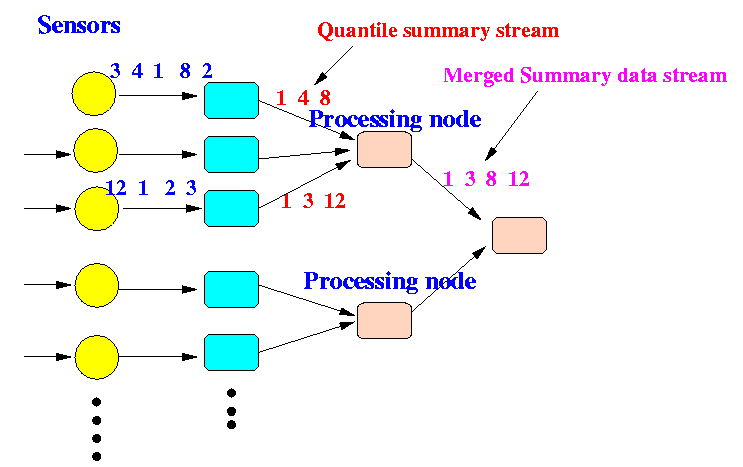
    Description:

    Sensors gather data (generate data stream) Each data stream is sent to a processing node Goal: minimize power consumption (wireless devices) by compressing (summarizing) the quantile-summary

    ---

  • Function of a processing node:

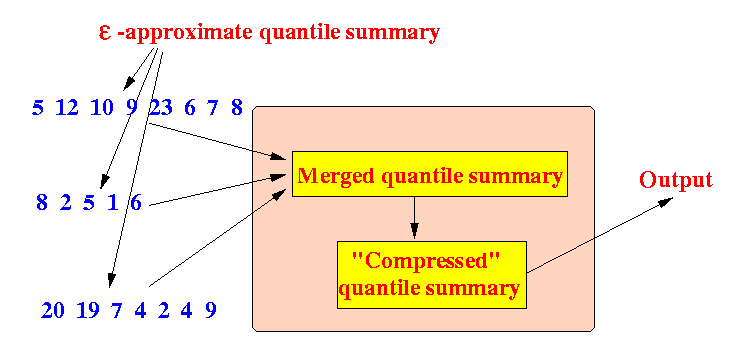
  • Operation:

    A node receives multiple quantile summaries It must form one quantile summary from the muliple summaries Then it must reduce the resulting summary into a quantile summary of size ≤ B+1 elements

  ---

  ---

• Pre-requisite
  • According to Corollary 1 in the firet Greenwald-Ghanna paper: click here

    If at any time n, the summary S(n) satisfies the property: maxall i ( gi + Δi )     ≤     2 ε n (Or:      maxall i ( gi + Δi ) / 2     ≤     ε n )               then we can use the summary S(n) to answer any φ-quantile query within ε n precision

    ---

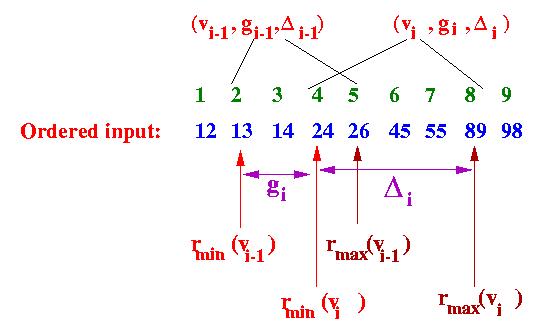
  • Relationship between g_i, Δ_i, r_min(v_i) and r_max(v_i) :

    ---

  • Corollary 1 can be re-phrased as follows: (See: click here )

    If at any time n, the summary S(n) satisfies the property: maxall i ( rmax(vi+1) - rmin(vi) )     ≤     2 ε n               then we can use the summary S(n) to answer any φ-quantile query within ε n precision

  ---

  ---

• Merging two ε-approximate quantile summaries
  • The merge operation on two ε-approximate quantile summaries is as follows:

    Let the two ε-approximate quantile summaries be: Q' = (x1, x2, ... xa) Q'' = (y1, y2, ... yb)              Let the combined result be: Q = (z1, z2, ... za+b)            Each xi, yi and zi is of the form: (v, rmin, rmax)              The Q = combine(Q', Q'') is: Merge sort the values v in Q' and Q'' Assign rmin(v) and rmax(v) to the sorted values using the algorithm described next.

  ---

  ---

• Assigning r_min(v) and r_max(v)
  • Assume:

    Q' = (x1, x2, ... xa) Q'' = (y1, y2, ... yb) Q = (z1, z2, ... za+b) = combine(Q', Q'')

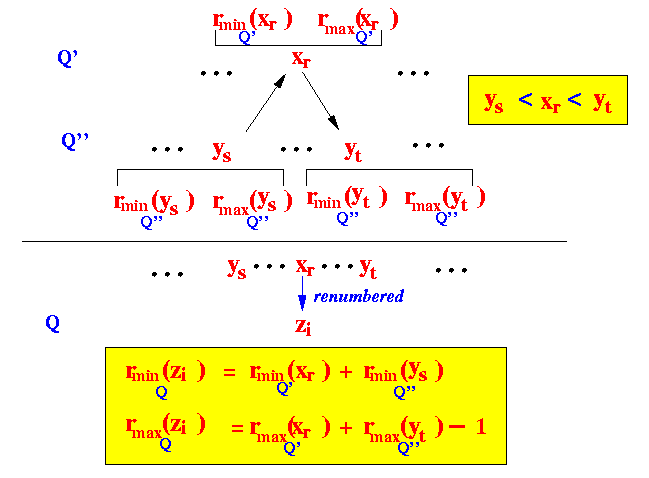
    Without loss of generality, assume the element x_r ∈ Q' is mapped to the element z_i ∈ Q

    Let ys ∈ Q'' be largest value that is < xr Let yt ∈ Q'' be smallest value that is > xr

    Then:

    rminQ(zi) = rminQ'(xr) if ys is undefined rminQ(zi) = rminQ'(xr) + rminQ''(ys) otherwise rmaxQ(zi) = rmaxQ'(xr) + rmaxQ''(ys) if yt is undefined rmaxQ(zi) = rmaxQ'(xr) + rmaxQ''(yt) - 1 otherwise

    ---

  • The following notes will go through the computation of r_minQ(z_i) and r_maxQ(z_i) a little bit more slower with a concrete example...

    ---

    ---

  • Case 1: the general case:

    xr ∈ Q' We can find a preceeding and a succeeding element in the other stream Let ys ∈ Q'' be largest value that is < xr Let yt ∈ Q'' be smallest value that is > xr Example: Q' = { 2:[1..1], 4:[3..4], 8:[5..6], 17:[8..8] } Q'' = { 1:[1..1], 7:[3..3], 12:[5..6], 15:[8..8] }              If xr = 8:[5..6] ∈ Q', then: ys = 7:3..3] ∈ Q'' yt = 12:5..6] ∈ Q'' If xr = 7:[3..3] ∈ Q'', then: ys = 4:3..4] ∈ Q' yt = 8:5..6] ∈ Q'

  • Suppose after merge sort, the element x_r become (renumbered) the element z_i ∈ Q

    Then the values r_min(z_i) and r_max(z_i) are defined as follows:

    ---

    ---

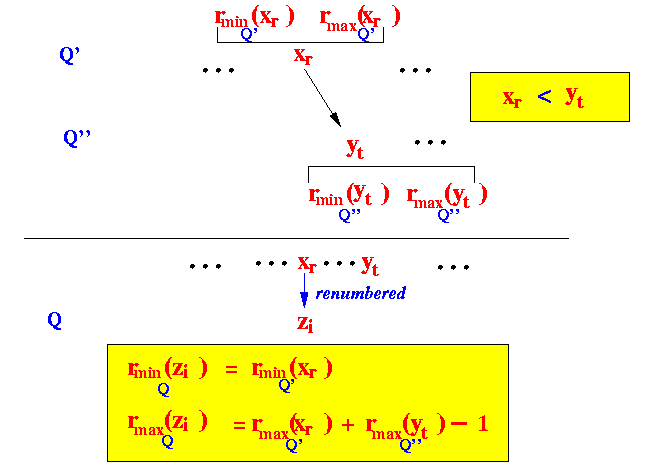
  • Case 2: the no preceeding element:

    xr ∈ Q' We cannot find a preceeding element There are only succeeding elements in the other stream Let yt ∈ Q' be smallest (first) value that is > xr Example: Q' = { 2:[1..1], 4:[3..4], 8:[5..6], 17:[8..8] } Q'' = { 1:[1..1], 7:[3..3], 12:[5..6], 15:[8..8] }              If xr = 1:[1..1] ∈ Q'', then: yt = 2:[1..1] ∈ Q'

  • Suppose after merge sort, the element x_r become (renumbered) the element z_i ∈ Q

    Then the values r_min(z_i) and r_max(z_i) are defined as follows:

    ---

    ---

  • Case 3: the no succeeding element:

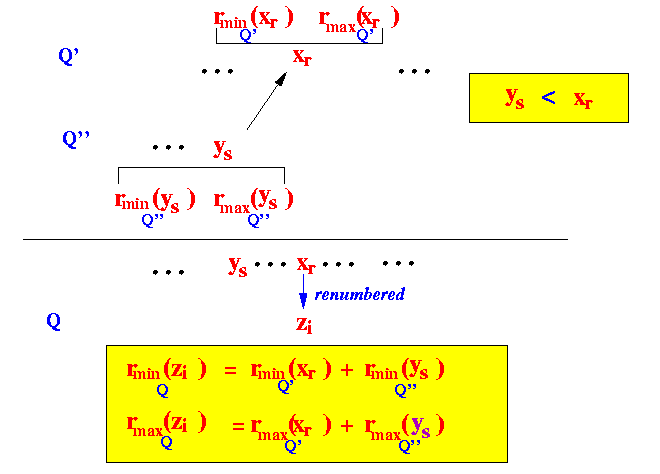
    xr ∈ Q' We cannot find a succeeding element There are only preceeding elements in the other stream Let ys ∈ Q' be largest (last) value that is < xr Example: Q' = { 2:[1..1], 4:[3..4], 8:[5..6], 17:[8..8] } Q'' = { 1:[1..1], 7:[3..3], 12:[5..6], 15:[8..8] }              If xr = 17:[8..8] ∈ Q', then: yt = 15:[8..8] ∈ Q''

  • Suppose after merge sort, the element x_r become (renumbered) the element z_i ∈ Q

    Then the values r_min(z_i) and r_max(z_i) are defined as follows:

  ---

  ---

• Example combine operation
  • Input sequences:

    Rank: 1 2 3 4 5 6 7 8 Sorted Stream 1: 2 3 4 6 7 8 10 17 Sorted Stream 2: 1 4 7 9 11 12 13 15 Q' = { 2:[1..1], 4:[3..4], 8:[5..6], 17:[8..8] } Q'' = { 1:[1..1], 7:[3..3], 12:[5..6], 15:[8..8] } (Q' and Q'' are quantile summaries with εN = 3 According to (click here): g + Δ = rmax(vi) - rmin(vi-1) ) Merged stream: Rank: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 2 3 4 4 6 7 7 8 9 10 11 12 13 15 17 Brown elements are from Stream 1 Red elements are from Stream 2

    ---

  • Combine algorithm:

    Input: Q' = { 2:[1..1], 4:[3..4], 8:[5..6], 17:[8..8] } Q'' = { 1:[1..1], 7:[3..3], 12:[5..6], 15:[8..8] } Steps: rminQ(1) = rminQ''(1) = 1 rmaxQ(1) = rmaxQ''(1) + rmaxQ'(2) - 1 = 1 + 1 - 1 = 1 rminQ(2) = rminQ'(2) + rminQ''(1) = 1 + 1 = 2 rmaxQ(2) = rmaxQ'(2) + rmaxQ''(7) - 1 = 1 + 3 - 1 = 2 rminQ(4) = rminQ'(4) + rminQ''(1) = 3 + 1 = 4 rmaxQ(4) = rmaxQ'(4) + rmaxQ''(7) - 1 = 4 + 3 - 1 = 6 rminQ(7) = rminQ''(7) + rminQ'(4) = 3 + 3 = 6 rmaxQ(7) = rmaxQ''(7) + rmaxQ'(8) - 1 = 3 + 6 - 1 = 8 rminQ(8) = rminQ'(8) + rminQ''(7) = 5 + 3 = 8 rmaxQ(8) = rmaxQ'(8) + rmaxQ''(12) - 1 = 6 + 6 - 1 = 11 rminQ(12) = rminQ''(12) + rminQ'(8) = 5 + 5 = 10 rmaxQ(12) = rmaxQ''(12) + rmaxQ'(17) - 1 = 6 + 8 - 1 = 13 rminQ(15) = rminQ''(15) + rminQ'(8) = 8 + 5 = 13 rmaxQ(15) = rmaxQ''(15) + rmaxQ'(17) - 1 = 8 + 8 - 1 = 15 rminQ(17) = rminQ'(17) + rminQ''(15) = 8 + 8 = 16 rmaxQ(17) = rmaxQ'(17) + rmaxQ''(15) = 8 + 8 = 16

    ---

    ---

  • Conclussion:

    Combined stream: Rank: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 2 3 4 4 6 7 7 8 9 10 11 12 13 15 17

    Summary:

    Q = 1:[1..1] 2[2..2] 4[4..6] 7[6..8] 8[8..11] 12[10..13] 15[13..15] 17[16..16] Max( rmax(vi) - rmin(vi-1) ) = 5 !!! However: N = 16, so εN is also twice as large !!!

    ---

  • You can verify that the merged summary is an εN quantile summary of the merged stream !!!

  ---

  ---

• Lemma 1: accuracy guarantee of the merge operation
  • Lemma 1:

    Let Q' be a ε'-approximate quantile summary for a set of values S' Let Q'' be a ε''-approximate quantile summary for a set of values S'' Then Q = combine(Q', Q'') produces an ε-approximate quantile summary for the set of values S' ∪ S'' with ε   =   max( ε' , ε'' )

    ---

    ---

  • Proof:

    Let: n' = | S' | and n'' = | S'' | Consider two arbitrary consecutive elements in Q': zi and              zi+1 By Corollary 1, we must show that: rmaxQ(zi+1) − rminQ(zi)   ≤   2 ε (n' + n'')              The proof is split into 2 cases: Case 1: zi and zi+1 are elements in the same set Case 2: zi and zi+1 are elements in the different sets

    ---

  • Proof of case 1: z_i and z_i+1 are elements in the same set

    Assume the values came from the set Q' Because there no value between zi and zi+1, the values that map into zi and zi+1 must be consecutive values in Q' Assume that the elements xr and xr+1 in Q' mapped into zi and zi+1 Q': .... xr xr+1 ... | | V V Q: .... zi zi+1 .... Let: ys be the largest element ∈ Q'' that is < xr yt be the smallest element ∈ Q'' that is > xr+1 Situation: Q'': ... ys yt ... Q': .... xr xr+1 ... | | V V Q: .... zi zi+1 .... Fact: ys and yt are consecutive elements in Q'' Because if there is an element between ys and yt, this element would come between xr and xr+1 !!! By the definition of rminQ(zi): rminQ(zi) = rminQ'(xr) if ys is undefined rminQ(zi) = rminQ'(xr) + rminQ''(ys) otherwise Hence: rminQ(zi) ≥ rminQ'(xr) And by the definition of rmaxQ(zi+1): rmaxQ(zi+1) = rmaxQ'(xr+1) + rmaxQ''(ys) if yt is undefined rmaxQ(zi+1) = rmaxQ'(xr+1) + rmaxQ''(yt) - 1 otherwise Since: rmaxQ''(yt) > rmaxQ''(ys) We have: rmaxQ(zi+1) ≤ rmaxQ'(xr+1) + rmaxQ''(yt) - 1 Therefore rmaxQ(zi+1) − rminQ(zi) ≤ [rmaxQ'(xr+1) + rmaxQ''(yt) - 1] - rminQ'(xr) = [rmaxQ'(xr+1) - rminQ'(xr)] + [rmaxQ''(yt) - 1] ≤ [rmaxQ'(xr+1) - rminQ'(xr)] + [rmaxQ''(yt) - rminQ''(yt-1)] (rminQ''(yt-1) ≥ 1 !) ≤ &epsilon'n' + &epsilon''n'' ≤ &epsilon n' + &epsilon n'' = &epsilon (n' + n'')

    ---

  • Proof of case 2: z_i and z_i+1 are elements in different sets

    Assume that: zi corresponds to xr ∈ Q' zi+1 corresponds to yt ∈ Q'' Situation: Q': .... xr ... Q'': .... yt ... | | V V Q: .... zi zi+1 .... Because there no value between zi and zi+1, we have that: xr is the largest value ∈ Q' that is < yt ∈ Q''     and, yt is the smallest value ∈ Q'' that is > xr ∈ Q' Moreover: Q': .... xr xr+1 ... Q'': .... yt-1 yt ... | | V V Q: .... zi zi+1 .... We also have: xr+1 is the smallest value ∈ Q' that is > yt ∈ Q'' (if xr+1 exists)     and, yt-1 is the largest value ∈ Q'' that is < xr ∈ Q' (if yt-1 exists) By the definition of rminQ(zi): rminQ(zi) = rminQ'(xr) if ys is undefined rminQ(zi) = rminQ'(xr) + rminQ''(yt-1) otherwise Hence: rminQ(zi) ≥ rminQ'(xr) And by the definition of rmaxQ(zi+1): rmaxQ(zi+1) = rmaxQ''(yt) + rmaxQ'(xr) if xr+1 is undefined rmaxQ(zi+1) = rmaxQ''(yt) + rmaxQ'(xr+1) - 1 otherwise Since: rmaxQ'(xr+1) > rmaxQ'(xr) We have: rmaxQ(zi+1) ≤ rmaxQ''(yt) + rmaxQ'(xr+1) - 1 Therefore rmaxQ(zi+1) − rminQ(zi) ≤ [rmaxQ''(yt) + rmaxQ'(xr+1) - 1] - rminQ'(xr) = [rmaxQ'(xr+1 - rminQ'(xr)] + [rmaxQ''(yt) - 1] ≤ [rmaxQ'(xr+1) - rminQ'(xr)] + [rmaxQ''(yt) - rminQ''(yt-1)] (rminQ''(yt-1) ≥ 1 !) ≤ &epsilon'n' + &epsilon''n'' ≤ &epsilon n' + &epsilon n'' = &epsilon (n' + n'')

  ---

  ---

• Corollary 1: merging multiple quantile summaries
  • Corollary 1:

    Let Q1, Q2, ..., Qk be quantile summaries such that: Qi is an εi-approximate quantile summary of a set Si Then: Let Q be a quantile summary produced by repeated applying the combine() operation (defined above) on Q1, Q2, ..., Qk Then, regardless of the sequence in which the combine() operation was applied, Q is an ε-approximate quantile summary of the set: S = &cupi=1..k( Si ) and: ε = mini=1..k( εi )

  ---

  ---

• Side note: How to use the quantile summary of the form v[r_min(v),r_max(v)]
  • Recall how to use an ε-approximate quantile summary, to answer a quantile queries:

    Given a quantile query for the element that ranks at the rth position Compute ⌊ ε × N ⌋ If r ≥ N - ⌊ ε × N ⌋, return vs-1 as answer If r < N - ⌊ ε × N ⌋, then: Find the first the smallest (first) value   rmax(vj)   that is larger than r + ⌊ ε × N ⌋ Return the value vj-1

  ---

  ---

• Reducing the size of the combine-result
  • Although the combine() operation produce an ε-approximate quantile summary, the size of the result is the sum of the original sets

    We may want to cut down on the number of entries used in the summary...

    ---

  • The prune operation can reduce the size of a quantile summary to a size of at most B+1 entries

    However, the reduction comes with at a cost:

    increased error margin

    ---

    ---

  • The prune operation:

    Input: S = quantile summary B = parameter QSummary Prune(QSummary S, int B) { QSummary R = ∅; // Result quantile summary for ( i = 1, (1/B)×|S|, (2/B)×|S|, (3/B)×|S|, ..., |S| ) { v = Query( S, i ); // Find the element at given ranking rmin( v ) = rmin( v ) in summary S; rmax( v ) = rmax( v ) in summary S; R = R ∪ { (v, rmin( v ), rmax( v ) } ; } return(R); }

  ---

  ---

• Lemma 2: the accuracy of the prune operation
  • Lemma 2:

    Let Q' be an ε'-approximate quantile summary of the set S Then Prune(Q', B) will return a (ε' + 1/(2B))-approximate quantile summary of the set S

  • Proof

    Consider each secussive pair of elements qi and qi+1 in Prune(Q', B): rmin( qi ) = rmin( qi ) in summary Q'; rmax( qi+1 ) = rmax( qi+1 ) in summary Q'; Then: qi qi+1 ^ ^ | | 1 (1/B)×|S| (i/B)×|S| ((i+1)/B)×|S| |S| |----------|-- .... ---|----------|----------|--- .... ----|----------| |<-------->| |S|/B / \ / \ / \ enlarged.... / \ / \ qi qi+1 ---|----|----|----|----|----|----|----|----|----|----|--- Q': vk vk+1 ... vm qi ranks # (i/B)×|S| qi+1 ranks # ((i+1)/B)×|S| Assume that: Element vk ranks # qi in set Q' Element vm ranks # qi+1 in set Q' Note that: m − k   ≤   (i/B)×|S| Recall that: rmin(vi) − rmin(vi-1) = gi      (See: click here ) gi = number of value covered by the entry vi           Then: rmax( qi+1 ) - rmin( qi ) = rmax( vm ) - rmin( vk ) = rmax( vm ) + + rmin( vm-1 ) - rmin( vm-1 ) + rmin( vm-2 ) - rmin( vm-2 ) + .... + rmin( vk+1 ) - rmin( vk+1 ) - rmin( vk ) rmax( qi+1 ) - rmin( qi ) = rmax( vm ) - rmin( vm-1 ) + rmin( vm-1 ) - rmin( vm-2 ) + rmin( vm-2 ) - rmin( vm-3 ) + .... + rmin( vk+2 ) - rmin( vk+1 ) + rmin( vk+1 ) - rmin( vk ) rmax( qi+1 ) - rmin( qi ) = rmax( vm ) - rmin( vm-1 ) + gm-1 + gm-2 + ... + gk+1 Because Q' is a ε'-approximate quantile summary, we have that: rmax( vm ) - rmin( vm-1 ) ≤ 2&epsilon'|S| The sum gm-1 + gm-2 + ... + gk+1 is number of elements covered by the entries vm-1, vm-2, ... , vk+1 This sum is ≤ (1/B)×|S| Therefore: rmax( qi+1 ) - rmin( qi ) ≤ 2&epsilon'|S| + (1/B)×|S| = 2 ( &epsilon' + 1/(2B)) × |S|