- Quantile
means ranking
- Suppose there are
N
elements (values)
- The φ-quantile is the element (value) that ranks at number ⌊ φ × N ⌋ among N elements
- Example:
Input set: 11 21 24 61 81 39 89 56 12 51 After sorting: 11 12 21 24 39 51 56 61 81 89 The 0.1-quantile = 11 The 0.2-quantile = 12 etc. Special case: The median = 0.5 quantile = 39
- The classic approach
to find quantiles
is to order (sort)
all the elements first
Then the sorted elements are scanned to find the one at position ⌊ φ × N ⌋
- Observations:
- Clearly, the classic approach
is an off-line algorithm
(all the elements must be present
in order to be sorted)
- This approach will not work for stream data
- Clearly, the classic approach
is an off-line algorithm
(all the elements must be present
in order to be sorted)
- If you want to find the
exact quantile (i.e., no error allowed),
then you must
use an
off-line algorithm
- To find the
φ-quantile
in a stream using
limited amount of memory,
we must allow for error...
- Greenwald & Khanna's paper presents
a beautiful algorithm
for finding
ε-approximate φ-quantiles
in a data stream.
- An ε-approximate quantile
is:
- the range of quantiles (ranking elements) that is within ε × N distince from the desired quantile.
- In other words, if the
desired quantile is
the φ-quantile
(which is the element that ranks at number
⌊ φ × N ⌋
among
N elements), then the
ε-approximate φ-quantile
is:
- any element
in the range
of elements that
rank between:
-
⌊ (φ − ε) × N ⌋
and
- ⌊ (φ + ε) × N ⌋
-
⌊ (φ − ε) × N ⌋
and
- any element
in the range
of elements that
rank between:
- Example: ε = 0.1
Input set: 11 21 24 61 81 39 89 56 12 51 After sorting: 11 12 21 24 39 51 56 61 81 89Special case: The median = 0.5 quantile = 39 The ε-approximate of the 0.5-quantile = {24, 39, 51}
The 0.1-quantile = 11 The ε-approximate of the 0.1-quantile = {11, 12} The 0.2-quantile = 12 The ε-approximate of the 0.2-quantile = {11, 12, 21} The 0.3-quantile = 21 The ε-approximate of the 0.3-quantile = {12, 21, 24} etc.
- Allowed error:
- Under the definition of the ε-approximate quantile, any value in the allowed range is a valid estimate for the desired quantile value
- Understand that the
ε-approximate φ-quantile
is a relative quantity:
- any element
in the range
of elements that
rank between:
-
⌊ (φ − ε) × N ⌋
and
- ⌊ (φ + ε) × N ⌋
-
⌊ (φ − ε) × N ⌋
and
- any element
in the range
of elements that
rank between:
- Notice that when
new elements
from the input stream are received,
the
value of N
increases !!
- The size of the set of ε-approximate quantiles increases with more elements in the stream !
Example: ε = 0.1
Input set: 11 21 24 61 81 39 89 56 12 51 After sorting: 11 12 21 24 39 51 56 61 81 89 ^ | #3
The 0.3-quantile = 21 (0.3*10 = 3) The ε-approximate of the 0.3-quantile = {12, 21, 24} (0.3-0.1)*10 = 2, (0.3+0.1)*10 = 4
Input set: 11 21 24 61 81 39 89 56 12 51 31 41 54 71 91 59 29 46 32 101 After sorting: 11 12 21 24 29 31 32 39 41 46 51 54 56 59 61 71 81 89 91 101 ^ | #6
The 0.3-quantile = 31 (0.3 *20 = 6) The ε-approximate of the 0.3-quantile = {24, 29, 31, 32, 39} (0.3-0.1)*20 = 4, (0.3+0.1)*20 = 8
- The key idea
of Greenwald & Khanna's algorithm is this:
- When N
increases, the
set of "correct" answers
(ε-approximate)
for the φ-quantile
increases
- As a result, you can remove some elements from the input stream and still retain the correct answer to the ε-approximate quantile query (= a query that asks for an ε-approximate quantile)
- When N
increases, the
set of "correct" answers
(ε-approximate)
for the φ-quantile
increases
- Example:
Input: 45 89 98 12 13 55 14 24 26 After sorting: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Input: 12 13 14 24 26 45 55 89 98Goal:
- maintain an ε-approximate φ-quantile for any value of φ.
- Suppose that
ε × N = 0
(no error allowed),
then we must maintain
every value to satisfy the
φ-quantile query
(Because every possible element can be queried and you cannot make any error !)
- But suppose that
ε × N = 1,
then we can
delete
some elements from the input and
still be
able to
satisfy the
φ-quantile query
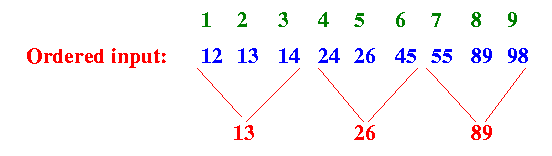
Original input: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 12 13 14 24 26 45 55 89 98 Retain only these elements: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 13 26 89 Approximate answers to quantile queries: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 13 13 13 26 26 26 89 89 89
Example usage:
- If the user requests the
"1st" element, we return
"13"
- this answer is allowed because the difference in the position between the actual value and the answer is 1 (within the error margin)
- If the user requests the
"4st" element, we return
"26"
- this answer is also allowed because the difference in the position between the actual value and the answer is 1 (within the error margin)
Conclusion:
- we do not need to maintain all 9 different values to answer the quantile query, but only 3 different values !!!
- If the user requests the
"1st" element, we return
"13"
- NOTE:
- The data structure
used to
represent
the "coverage"
information
is very important
(you will see this fact when we discuss the algorithm)
- We will look at the representation data structure first
- The data structure
used to
represent
the "coverage"
information
is very important
- To design an algorithm,
you must first
design an
adequate data structure
to maintain the information
used by the algorithm
- Conside how
you would store information
so you can answer
a
φ-quantile query:
Original input: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 12 13 14 24 26 45 55 89 98 Retain only these elements: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 13 26 89 Approximate answers to quantile queries: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 13 13 13 26 26 26 89 89 89
- An obvious way to
represent the
φ-quantile
information is as follows:
( [v1,min1,max1], [v2,min2,max2], ..., [vm,minm,maxm] ) where: vi = the value that covers the φ-quantile range mini = start position of the φ-quantile range maxi = ending position of the φ-quantile range
Example: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 13 13 13 26 26 26 89 89 89 is represented as: [13, 1, 3] [26, 4, 6] [89, 7, 9] ( [13, 1, 3] means the value 13 covers the rank position 1..3 )
- Problem with the above representation:
not easy to update
Suppose the input stream is: 12 13 14 24 26 45 55 89 98 ...(more data coming) (For ease of understanding, here is the sorted list of the input number: 12 13 14 24 26 45 55 89 98 ) The algorithm represents the current state with: [13, 1, 3] [26, 4, 6] [89, 7, 9]Now suppose the next arriving value is 17:
The input stream is now: 12 13 14 24 26 45 55 89 98 17...(more data coming) (For ease of understanding, here is the sorted list of the input number: 12 13 14 17 24 26 45 55 89 98 ) The algorithm must modify the state in the data structure to: [13, 1, 3] [17, 4, 4] [26, 5, 7] [89, 8, 10] ^^^^^^^^^^ ^^^^^ ^^^^^ inserts 17 but must also change indices in later entries !!!
This data structure requires a large number of operations per inserted value
Although it is useful, it is not efficient
- A better suited
data structure
to represent
the φ-quantile
information:
( [v1,g1], [v2,g2], ..., [vm,gm] ) where: vi = the value that covers the φ-quantile range gi = number of positions covered by the value
Example: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 13 13 13 26 26 26 89 89 89 is represented as: [13, 3] [26, 3] [89, 3] [13, 3] means the value 13 covers the first 3 positions [26, 3] means the value 13 covers the next 3 positions [89, 3] means the value 13 covers the "next next" 3 positionsNow suppose the next arriving value is 17:
The input stream is now: 12 13 14 24 26 45 55 89 98 17...(more data coming) (For ease of understanding, here is the sorted list of the input number: 12 13 14 17 24 26 45 55 89 98 ) The algorithm must modify the state in the data structure to: [13, 3] [17, 1] [26, 3] [89, 3] ^^^^^^^ ^^^ ^^^ inserts 17 but the other information does not need to be updated !!!How to read the data structure:
-
[13, 3] [17, 1] [26, 3] [89, 3]
- Ranking and answer:
- 13
- 13
- 13
- 17
- 26
- 26
- 26
- 89
- 89
- 89
-
[13, 3] [17, 1] [26, 3] [89, 3]
- Problem with this data structure:
- It does not contain enough information to let you cut away (delete) unnecessary entries
- "Coverage" provided by a value:
Original input: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 12 13 14 24 26 45 55 89 98 Retain only these elements: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 13 26 89 Coverage provided by each entry: Rank: 1 2 3 4 5 6 7 8 9 -------+---------------------------- Ranked: 13 13 13 26 26 26 89 89 89
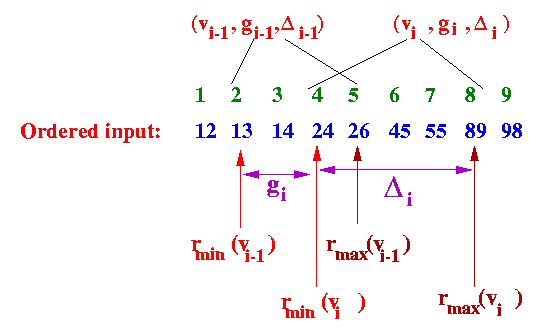
- Definitions:
- rmin(v) = lower bound on the rank that value v can be used as answer to a quantile query
- rmax(v) = upper bound on the rank that value v can be used as answer to a quantile query
Example: in the above summary
- rmin(13) = 1 rmax(13) = 3
- rmin(26) = 4 rmax(26) = 6
- rmin(89) = 6 rmax(89) = 9
Graphically:
- In general,
the "coverage"
of the different value will
overlap:
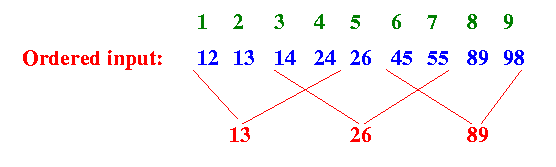
- More definitions:
- The data structure used by
Greenwald & Khanna's algorithm
is as follows:
( [v0,g0,Δ0], [v1,g1,Δ1], [v2,g2,Δ2], ..., [vs-1,gs-1,Δs-1] ) where: vi = the value that covers the φ-quantile range gi = see definition above Δi = see definition above
NOTE: v0 ≤ v1 ≤ ... ≤ vs-1 v0 = smallest value in stream vs-1 = largest value in stream
- Important:
-
The algorithm
always
maintains
the following values:
- v0 = smallest value seen so far
- vs-1 = largest value seen so far
-
The algorithm
always
maintains
the following values:
- Fact 1:
rmin(vi) =
∑ij=0 gi
- By definition:
rmin(vi) −
rmin(vi-1)
=
gi
- Hence:
- rmin(vi) = gi + rmin(vi-1)
- rmin(vi) = gi + gi-1 + rmin(vi-2)
- rmin(vi) = gi + gi-1 + gi-2 + rmin(vi-3)
- ...
- rmin(vi) = gi + gi-1 + gi-2 + .. rmin(v0)
There is no -1 element, so the value of g0 is undefined
- We can define to to be:
-
g0 = rmin(v0) = 1
In fact, that's the value that the GK algorithm will assign to g0
- By definition:
rmin(vi) −
rmin(vi-1)
=
gi
- Fact 2:
rmax(vi) =
∑j=0i gi
+ Δi
- This fact follows
directly from
fact 1 and
the definition:
- Δi = rmax(vi) − rmin(vi)
- This fact follows
directly from
fact 1 and
the definition:
- Fact 3:
g0 + g1 + ... + gs-1 = N
-
rmax(vs-1) = N
because
the summary must cover all
N values
- From Fact 2 we have:
- rmax(vs-1) = ∑j=0s-1 gi + Δs-1
- You will see that the algorithm
sets
Δs-1
= 0
So: rmax(vs-1) = ∑j=0s-1 gi = N
-
rmax(vs-1) = N
because
the summary must cover all
N values
- Example reading the summary data:
(v0, g0, Δ0) (v1, g1, Δ1) (v2, g2, Δ2) (5, 1, 4) (7, 3, 3) (10, 4, 0) rmin(v0) = 1 rmax(v0) = 1 + 4 = 5 rmin(v1) = 1 + 3 = 4 rmax(v0) = 4 + 3 = 7 rmin(v1) = 4 + 4 = 8 rmax(v0) = 8 + 0 = 8
Ranking: 1 2 3 4 5 6 7 8 5 5 5 5 5 7 7 7 7 10
- Proposition 1:
- Given a quantile summary S
in the above form.
- Let e =
maxall i(gi + Δi) / 2
Claim:
-
Using the summary S, we can
identify
a φ-quantile within
an error of
e =
maxall i(gi + Δi) / 2
- Given a quantile summary S
in the above form.
- I find this
interpretation
of the Corollary
easier to "parse":
- Let
r = φ × N
So the φ-quantile query asks:
- Find the element that ranks at position r in the input stream of N elements
- The Corollary claims that such query
can be answered with
an error of
e =
maxall i(gi + Δi) / 2
Graphically:
The element that ranks at position r is: Ranking: 1 2 .... r-e r r+e . . . . . . . . . . . . . . . . . . . . . . . . . . . . ^ | r
The allowable values that has an error within e are: Ranking: 1 2 .... r-e r r+e . . . . . . . . . . . . . . . . . . . . . . . . . . . . ^ | r - Then we can satisfy
this query
with
an error of
e =
maxall i(gi + Δi) / 2
if we can
find a value vi
such that:
Ranking: 1 2 .... r-e r r+e . . . . . . . . . . . . . . . . . . . . . . . . . . . . ^ ^ | | rmin(vi) rmax(vi) r-e ≤ rmin(vi) ∧ rmax(vi) ≤ r+eThe reason is as follows:
- By the definition of the
values
rmin(vi)
and
rmin(vi),
the value vi is
a correct answer
to any quantile query
that is within the range
[rmin(vi)..rmax(vi)]
- If the range [rmin(vi)..rmax(vi)] lies within the allowable range [r-e..r+e], the value vi is an allowable answer to the quantile query that is within the acceptable error range [r-e..r+e]
- By the definition of the
values
rmin(vi)
and
rmin(vi),
the value vi is
a correct answer
to any quantile query
that is within the range
[rmin(vi)..rmax(vi)]
- We must show that:
- There is always such an
element vi with
the property that:
- r-e ≤ rmin(vi) and;
- rmax(vi) ≤ r+e
- There is always such an
element vi with
the property that:
- Let
r = φ × N
- Proof:
- We split r into
2 ranges:
1 n-e n |-----------------------------------------+---------+ r ≤ n-e r > n-e
Case 1: r > n-e
- When
r > n-e, the
acceptable range of
values that can be used to
answer the quantile query
are:
1 n-e n |---------+--------------------------------+---------+ acceptable range <---------^---------> | r - Notice that the acceptable range
always
include the
largest value in the stream
- The algorithm always
retains
the largest value
vs-1
seen in the input
- Therefore, we can
always use the
largest value as
an acceptable answer
to the
quantile query
Case 2: r ≤ n-e
- In this case, find
the smallest index j
such that:
- rmax(vj) > r + e
- Graphically:
rmax(vj-1) rmax(vj) | | v v +--------------------------------------------+-------| <---------^---------> e | e r Notice that: rmax(vj-1) ≤ r + e (We have one half of the inequality done)
- From that fact that:
-
rmax(vj) -
rmin(vj-1) =
gj + Δj
and
- gj + Δj ≤ maxall i ( gi + Δi ) = 2 × e
we have:
rmin(vj-1) | | gj + Δj ≤ 2 × e |<----------------> | rmax(vj-1) rmax(vj) | | | v v v +--------------------------------------------+-------| <---------^---------> e | e r Thus: r-e ≤ rmin(vj-1) (We have the other half of the inequality done !)
-
rmax(vj) -
rmin(vj-1) =
gj + Δj
and
- Conclusion:
- The value vj-1 can be used to answer the quantile query !
- We split r into
2 ranges:
- Corollary 1:
- If at any time n,
the summary S(n)
satisfies the property:
-
maxall i ( gi + Δi )
≤
2 ε n
(Or: maxall i ( gi + Δi ) / 2 ≤ ε n )
then we can use the summary S(n) to answer any φ-quantile query within ε n precision
-
maxall i ( gi + Δi )
≤
2 ε n
- If at any time n,
the summary S(n)
satisfies the property:
- Proof:
- Proposition 1 states that
a summary S can be used to
answer any quantile query
within an error of
maxall i ( gi + Δi ) / 2
- If we make sure that:
- maxall i ( gi + Δi ) / 2 ≤ ε n
all the time, then:
- We can answer any quantile query within an error that is at least as good as ε n
- Proposition 1 states that
a summary S can be used to
answer any quantile query
within an error of
maxall i ( gi + Δi ) / 2
- Structure of the GK alorithm:
N = 0; while ( not EOS ) { /* ----------------------- Delete phase ----------------------- */ if ( N mod ( 1/(2 ε) ) == 0 ) delete elements from summary; v = next value in stream; /* ----------------------- Insert phase ----------------------- */ insert v into summary; N++; }
- We saw above that the values
gi
and
Δi
has well-defined meanings
Important:
- Inserting an arriving value must maintain the consistency of the information in the summary
- The insert step
in Greenwald & Khanna's Algorithm is as follows:
v = next value in input /* -------------------------------------------- Find insert position for v in S -------------------------------------------- */ Find a tuple (vi, gi, Δi) ∈ S such that: vi-1 ≤ v < vi if ( v < v0 || v > vs-1 ) Δ = 0; // New min or max value else Δ = gi + Δi - 1; INSERT "(v, 1, Δ)" into S between vi and vi+1;
- Claim:
- After inserting
(v, 1, Δ)
into the summary S, the
properties
-
rmin(vi) =
∑j=0i gi
-
rmax(vi) =
∑j=0i gi
+ Δi
- g0 + g1 + ... + gs-1 = N
are preserved
-
rmin(vi) =
∑j=0i gi
Proof:
- The 3 facts depends on
g to keep an accurate
count of the elements in the summary.
- Because v is
inserted after vi-1
the counts related to
elements 1, 2, ..., i-1
are unchanged
Since g = 1 is not added to these values, the counts are unchanged
- Because v is
inserted before vi
the counts related to
elements v, v+1, ..., s-1
are increased by 1
Since g = 1 is added to these values, the counts are increased by 1
- After inserting
(v, 1, Δ)
into the summary S, the
properties
- Claim:
- After inserting (v, 1, Δ) into the summary S, the property maxall i(gi + Δi) / 2 < &epsilon × n is maintained.
Proof:
- Suppose v was
inserted between
vi-1
and
vi
Summary: (vi-1, gi-1, Δi-1) (v, 1, Δ) (vi, gi, Δi) ------------------+---------------+--------------+--------------
- There are 2 new values of
gj + Δj
(see: click here)
to consider:
-
g + Δ =
rmax(v) -
rmin(vi-1)
- gi + Δi = rmax(vi) - rmin(v)
-
g + Δ =
rmax(v) -
rmin(vi-1)
-
g + Δ
- The algorithm assigns:
- g = 1 and
- Δ = 0 or gi + Δi - 1
- Therefore:
g + Δ =
1 +
(gi + Δi - 1) =
gi + Δi
- This was a value in the old summary and will satisfy the property
- The algorithm assigns:
-
gi + Δi
- The algorithm assigns:
g = 1
and
Δ = gi + Δi - 1
- Thus:
- g + Δ = gi + Δi
- This was a value in the old summary and will satisfy the property
- The algorithm assigns:
g = 1
and
Δ = gi + Δi - 1
- The goal of the
quantile summary
is to
provide information
to answer
a φ-quantile query
with
ε accuracy
- We saw
in Corollary 1
(See:
click here)
that in order to
provide information
to answer
a φ-quantile query
with
ε accuracy,
we must ensure that:
- maxall i ( gi + Δi ) ≤ 2 ε n
So as long as we maintain this property, the information in the summary will allow us to answer any φ-quantile query with ε accuracy
- The most important part
of the algorithm is the
delete part
But it is also the most complex part of the algorithm
- I will introduce the
delete operation
in a piecemeal fashion
- hopefulling the algorithm will be easier to
understand in this manner
I will discuss deleting one tuple first...
- Claim:
- Consider the summary:
..... (vi, gi, Δi), (vi+1, gi+1, Δi+1) .... - If
gi +
gi+1 + Δi+1
≤
2 ε n
,
we can
replace:
..... (vi, gi, Δi), (vi+1, gi+1, Δi+1) .... by: ..... (vi+1, gi+gi+1, Δi+1) ....and the resulting summary can answer any φ-quantile query with ε accuracy
Proof:
- The proposed change does not alter
the property
maxall k ( gk + Δk )
≤
2 ε n
because:
-
gk + Δk
are unchanged
for k != i or i+1
Hence,
-
gk + Δk
≤
2 ε n
for k != i or i+1
- The new entry added to
the summary is
(vi, gi+gi+1, Δi+1)
and it's
sum is:
- (gi+gi+1) + Δi
And it was given that:
- gi + gi+1 + Δi+1 ≤ 2 ε n
-
gk + Δk
are unchanged
for k != i or i+1
- Therefore: the
property
maxall k ( gk + Δk )
≤
2 ε n
still holds !!!
And according to Corollary 1 (click here ) the resulting summary can answer any φ-quantile query with ε accuracy
- Consider the summary:
- Multiple tuples can be
"merged" into
one tuples if a
similar condition is
satisfied !!!
- Claim:
- Consider the summary:
..... (vj, gj, Δj) ... (vi, gi, Δi), (vi+1, gi+1, Δi+1) .... - If:
-
gj + ...
gi +
gi+1 + Δi+1
≤
2 ε n
we can replace:
..... (vj, gj, Δj) ... (vi, gi, Δi), (vi+1, gi+1, Δi+1) .... by: ..... (vi+1, gj + ... + gi+gi+1, Δi+1) ....and the resulting summary can answer any φ-quantile query with ε accuracy
Proof:
- The proposed change does not alter
the property
maxall k ( gk + Δk )
≤
2 ε n
because:
-
gk + Δk
are unchanged
for k < j or k > i+1
Hence,
-
gk + Δk
≤
2 ε n
for k < j or k > i+1
- The new entry added to
the summary is
(vi, gj+ ... + gi+gi+1, Δi+1)
and it's
sum is:
- ( gj+ ... + gi+gi+1) + Δi
And it was given that:
- gj+ ... + gi + gi+1 + Δi+1 ≤ 2 ε n
-
gk + Δk
are unchanged
for k < j or k > i+1
- Therefore: the
property
maxall k ( gk + Δk )
≤
2 ε n
still holds !!!
And according to Corollary 1 (click here ) the resulting summary can answer any φ-quantile query with ε accuracy
- Consider the summary:
- NOTE:
- The value of Δ in the summary is not updated after a tuple is inserted into the summary
- This fact is obvious from the delete
algorithm:
- When 2 or more tuples are merged, the value of g is changed, but the value of Δ is unchanged
- We will see that
Δ will
play a role in
determine which tuple
to keep
in the summary....
- So far, we have only
considered
correctness:
- How to insert a
new value into the summary
so that the
new summary
correctly reflect
the new state
- How to delete (merge) two or more entries into one entry so that the new summary correctly reflect the new state
- How to insert a
new value into the summary
so that the
new summary
correctly reflect
the new state
- With this knowledge, we can
already construct
a correct quantiles algorithm:
*** ε is the margin error (a parameter of the algorithm) S = {}; // S contains the summary structure, which is: // <(v0, g0, Δ0), (v1, g1, Δ1) ... > // NOTE: S is an ordered list !!! N = 0; // Number of items processed while ( not EOS ) { /* --------------------------------------------- Delete phase: executed once every 1/(2×ε) insertions --------------------------------------------- */ if ( N % ⌊1/(2×ε)⌋ == 0 ) { /* -------------------------------------------------- Delete unnecessary entries in summary (while keeping the smallest and largest elements) -------------------------------------------------- */ for ( i = s-1; i ≥ 2; i = j - 1 ) { j = i-1; while ( j ≥ 1 && gj + ... + gi + Δi < 2εN ) { j--; } j++; // We went one index too far in the while... if ( j < i ) { replace entries j, .., i with the entry (vi, gj+ ... + gi, Δi); } } } /* ------------------------------------ Insert phase ------------------------------------ */ v = next value in input /* -------------------------------------------- Find insert position for v in S -------------------------------------------- */ Find a tuple (vi, gi, Δi) ∈ S such that: vi-1 ≤ v < vi if ( v is inserted at the head or tail of S ) Δ = 0; else Δ = gi + Δi - 1 // This is the allowable "wiggle room" INSERT "(v, 1, Δ)" into S between vi-1 and vi; N++; }
- The quantile summary is
used to answer quantile queries
- Given a ε-approximate
quantile summary,
how do we use it to
answer a
quantile queries ?
- Answer:
- See the proof of Proposition 1 ( click here )
- Procedure summary:
- Given a quantile query
for the element that
ranks at the rth position
- Compute ⌊ ε × N ⌋
- If r ≥
N - ⌊ ε × N ⌋,
return
vs-1
as answer
- If r <
N - ⌊ ε × N ⌋,
then:
- Find the first the smallest (first)
value rmax(vj)
that is larger
than
r + ⌊ ε × N ⌋
- Return the value vj-1
- Find the first the smallest (first)
value rmax(vj)
that is larger
than
r + ⌊ ε × N ⌋
- Given a quantile query
for the element that
ranks at the rth position