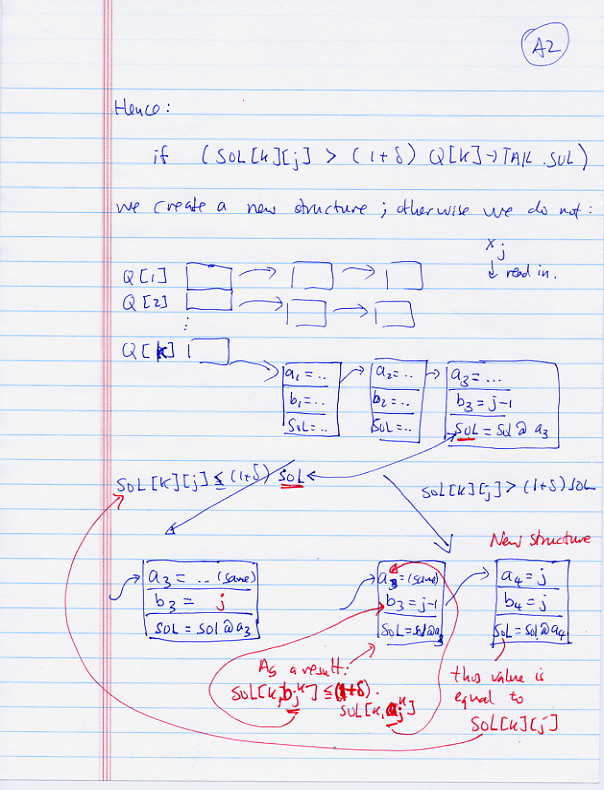
- Denote:
- OPT[k][i] = the error in the V-optimal histogram using k buckets covering the input data x1 .. xi
- We saw that Jagadish's algorithm
searches through the
following values to find
OPT[k][i] :
- OPT[k-1][1] + SqError(2,i)
- OPT[k-1][2] + SqError(3,i)
- OPT[k-1][3] + SqError(4,i)
- ...
- OPT[k-1][i-1] + SqError(i,i)
(where SqError(a,b) = the minimum squared error sum of input values for xa... xb - which is also the mininum error for a single bucket histogram on these values).
- For example:
Input data: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 OPT[k][i]: i: 1 2 3 4 5 6 7 8 9 10 11 12 13 k 1 0 0.5 2.0 5.0 10.0 17.5 28.0 42.0 60.0 82.5 110.0 143.0 182.0 ... 2 0 0.0 0.5 1.0 2.5 4.0 7.0 10.0 15.0 20.0 27.5 35.0 45.5 ... 3 0 0 0.0 0.5 1.0 1.5 3.0 4.5 6.0 9.0 12.0 15.0 20.0 ...
- Program used to generate the data above:

- Prog file: click here
- Input file 1 (2 bucket histogram): click here
- Input file 2 (3 bucket histogram): click here
- Guha made this
observation
- The values OPT[k][i]
in a row
(i.e., increasing i
in data is increasing very
slowly
- and therefore, the values values OPT[k][i] can be ideally be approximated by... a histogram !!! (what else ?)
Example:
Input data: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 OPT[k][i]: i: 1 2 3 4 5 6 7 8 9 10 11 12 13 k 1 0 0.5 2.0 5.0 10.0 17.5 28.0 42.0 60.0 82.5 110.0 143.0 182.0 ... 2 0 0.0 0.5 1.0 2.5 4.0 7.0 10.0 15.0 20.0 27.5 35.0 45.5 ... 2' 0 0 0 0 2.5 2.5 7.0 7.0 7.0 20.0 20.0 20.0 20.0 3 0 0 0.0 0.5 1.0 1.5 3.0 4.5 6.0 9.0 12.0 15.0 20.0 ...
- The values OPT[k][i]
in a row
(i.e., increasing i
in data is increasing very
slowly
- Note:
- We will use the first value
in a histogram bucket
to represent
all values in the bucket...
- We do not even attempt to
find the average
of the values in the bucket
to minimize the error
Guha decide to do this for efficiency reasons: because the values are slowly increasing anyway...
- We will use the first value
in a histogram bucket
to represent
all values in the bucket...
- Consequence:
- The resulting historgram
will not have
the smallest possible squarred
error V-optimal histogram
- The resulting historgram does "resemble" (= approximates) the V-optimal histogram
- The resulting historgram
will not have
the smallest possible squarred
error V-optimal histogram
- Advantages:
- Uses less memory
(histogram is more compact that an array)
- Runs faster (don't need to compute all the squared errors)
- Uses less memory
(histogram is more compact that an array)
- Reason to use approximation for OPT[k][i]:
- The V-optimal histogram
is only a
approximation
of the values it summarizes (represents)
- Since the values are already inexact, there is not much harm if we use a less exact approximation - as long as we can control the error
- The V-optimal histogram
is only a
approximation
of the values it summarizes (represents)
- Requirement of the approximation:
- We need to provide a guarantee
of the accurate
of the approximation
used.
- In fact, we want to let the user
decide how to
trade off
between:
- the running time of the algorithm
- and the accuracy achieved.
- We need to provide a guarantee
of the accurate
of the approximation
used.
- Controlling the error
in the histogram representation
of
OPT[k][i]:
- We can control the error
by using more buckets
- I.e., the histogram is not restricted to use a fixed number of buckets
- We can control the error
by using more buckets
- Example: using 4 buckets to
approximate OPT[k][2]:
Input data: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 OPT[k][i]: i: 1 2 3 4 5 6 7 8 9 10 11 12 13 k 1 0 0.5 2.0 5.0 10.0 17.5 28.0 42.0 60.0 82.5 110.0 143.0 182.0 ... 2 0 0.0 0.5 1.0 2.5 4.0 7.0 10.0 15.0 20.0 27.5 35.0 45.5 ... 2' 0 0 0 0 2.5 2.5 7.0 7.0 7.0 20.0 20.0 20.0 20.0 Err: 0 0 0.5 1.0 0 1.5 0 3.0 8.0 0 7.5 15.0 25.0 3 0 0 0.0 0.5 1.0 1.5 3.0 4.5 6.0 9.0 12.0 15.0 20.0 ...
The error can be reduced by using 5 buckets to approximate OPT[k][2]: :
Input data: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 OPT[k][i]: i: 1 2 3 4 5 6 7 8 9 10 11 12 13 k 1 0 0.5 2.0 5.0 10.0 17.5 28.0 42.0 60.0 82.5 110.0 143.0 182.0 ... 2 0 0.0 0.5 1.0 2.5 4.0 7.0 10.0 15.0 20.0 27.5 35.0 45.5 ... 2' 0 0 0 0 2.5 2.5 7.0 7.0 7.0 20.0 20.0 35.0 35.0 Err: 0 0 0.5 1.0 0 1.5 0 3.0 8.0 0 7.5 0.0 10.0 3 0 0 0.0 0.5 1.0 1.5 3.0 4.5 6.0 9.0 12.0 15.0 20.0 ...
- Formal specification:
Notations: OPT[k][i] and SOL[i][k]:
Input data: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 OPT[k][i]: i: 1 2 3 4 5 6 7 8 9 10 11 12 13 k 1 0 0.5 2.0 5.0 10.0 17.5 28.0 42.0 60.0 82.5 110.0 143.0 182.0 ... --> OPT[2][i] 0 0.0 0.5 1.0 2.5 4.0 7.0 10.0 15.0 20.0 27.5 35.0 45.5 ... --> Sol[2][i] 0 0 0 0 2.5 2.5 7.0 7.0 7.0 20.0 20.0 35.0 35.0 Err: 0 0 0.5 1.0 0 1.5 0 3.0 8.0 0 7.5 0.0 10.0 3 0 0 0.0 0.5 1.0 1.5 3.0 4.5 6.0 9.0 12.0 15.0 20.0 ...How to ensure accuracy:
- Let p =
number of bucket
in the Histogram
- Denote:
[ajp,bjp]
are end points
of an interval whose
OPT[p][..]
are represented by the
same
value
- We require that:
OPT[p][bjp] - OPT[p][ajp] ----------------------------- ≤ δ (δ > 0) OPT[p][ajp]for some pre-selected value of δ
- Let p =
number of bucket
in the Histogram
- Pictorially:
Histogram with p backets used to approximate OPT[p][..]: x OPT[p][bjp] | x OPT[p][ajp] | | | | | | | ----+-----------------------+------- ajp <-----------------> bjp
The expression: OPT[p][bjp] - OPT[p][ajp] ----------------------------- OPT[p][ajp] is the relative errorIn other words:
- The relative error in one bucket is at most δ
- Note: the
relative error constraint
can be re-written as follows:
OPT[p][bjp] - OPT[p][ajp] ----------------------------- < δ OPT[p][ajp] <==> OPT[p][bjp] - OPT[p][ajp] < δ × OPT[p][ajp] <==> OPT[p][bjp] < (1 + δ) OPT[p][ajp]
- Example: δ = 2
Requirement:
- OPT[p][bjp] ≤ 2 × OPT[p][ajp]
Input data: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 OPT[k][i]: i: 1 2 3 4 5 6 7 8 9 10 11 12 13 k 1 0 0.5 2.0 5.0 10.0 17.5 28.0 42.0 60.0 82.5 110.0 143.0 182.0 ... --> OPT[2][i] 0 0.0 0.5 1.0 2.5 4.0 7.0 10.0 15.0 20.0 27.5 35.0 45.5 ... --> Sol[2][i] 0 0.0 0.5 0.5 2.5 2.5 7.0 7.0 15.0 15.0 27.5 27.5 27.5 ... +------+ +-------+ +---------+ +---------++----------+ +-----------------+
Sol[2][i] will be used to compute further - these values will change: 3 0 0 0.0 0.5 1.0 1.5 3.0 4.5 6.0 9.0 12.0 15.0 20.0 ...
- Theorem 3
of their paper will show that
the histogram constructed by the algorithm will
provide an accuracy guarantee
(stated and proved below
click here
- Consider the following input:
- f1 = 4
- f2 = 2
- f3 = 3
- f4 = 6
- f5 = 5
- f6 = 6
- f7 = 12
- f8 = 16
Problem: construct an approximate V-optimal histogram with B = 3 buckets
- Step 1: construct
V-optimal histogram
with
B = 1 bucket
-
Note:
This is just minimize the squared error
, so we do not
need to approximate and
can use the result from
this webpage:
click here
Histogram with 1 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0.0 | 2.0 | 2.0 | 8.75 | 10.0 | 13.3 | 63.7 | 161.5|
- Step 2: construct
approximate V-optimal histogram
with
B = 2 bucket
- Initially:
Input: 4 2 3 6 5 6 12 16
Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0.0 | 0.0 | ?? | ?? | ?? | ?? | ?? | ?? | +----------+ 0.0 curr bucket
- To find the best bucket partition
for values 4 2 3, we try:
[ 4 2 ] [ 3 ] ===> MinError[1][2] + 0 [ 4 ] [ 2 3 ] ===> MinError[1][1] + (2 - 2.5)2 + (3 - 2.5)2 | | +-------+ 1 bucket optimal histogram Using the result from the 1 bucket optimal histogram: [ 4 2 ] [ 3 ] ===> 2.0 + 0 = 2.0 [ 4 ] [ 2 3 ] ===> 0.0 + 0.5 = 0.5 <---- MinResult: larger than 2*0 --> start a new bucket with value = 0.5
Input: 4 2 3 6 5 6 12 16
Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0.0 | 0.0 | 0.5 | ?? | ?? | ?? | ?? | ?? | +----------+ +----+ 0.0 0.5
- To find the best bucket partition
for values 4 2 3 6, we try:
[ 4 2 3 ] [ 6 ] ===> MinError[1][3] + 0 [ 4 2 ] [ 3 6 ] ===> MinError[1][2] + (3 - 4.5)2 + (6 - 4.5)2 [ 4 ] [ 2 3 6 ] ===> MinError[1][1] + (2 - 3.66)2 + (3 - 3.66)2 + (6 - 3.66)2 | | +---------+ 1 bucket optimal histogram Using the result from the 1 bucket optimal histogram: [ 4 2 3 ] [ 6 ] ===> 2.0 + 0 = 2.0 <--- Min [ 4 2 ] [ 3 6 ] ===> 2.0 + 4.5 = 6.5 [ 4 ] [ 2 3 6 ] ===> 0.0 + 8.666 = 8.666Result: greater than 2*0.5 --> start a new bucket with value = 2.0
Input: 4 2 3 6 5 6 12 16
Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0.0 | 0.0 | 0.5 | 2.0 | ?? | ?? | ?? | ?? | +----------+ +----+ +----+ 0.0 0.5 2.0
- To find the best bucket partition
for values 4 2 3 6 5, we try:
[ 4 2 3 6 ] [ 5 ] ===> MinError[1][4] + 0 [ 4 2 3 ] [ 6 5 ] ===> MinError[1][3] + (6 - 5.5)2 + (5 - 5.5)2 [ 4 2 ] [ 3 6 5 ] ===> MinError[1][2] + (3 - 4.66)2 + (6 - 4.66)2 + (5 - 4.66)2 [ 4 ] [ 2 3 6 5 ] ===> MinError[1][1] + (2 - 4)2 + (3 - 4)2 + (6 - 4)2 + (5 - 4)2 | | +-----------+ 1 bucket optimal histogram Using the result from the 1 bucket optimal histogram: [ 4 2 3 6 ] [ 5 ] ===> 8.75 + 0 = 8.75 [ 4 2 3 ] [ 6 5 ] ===> 2.0 + 0.5 = 2.5 <--- Min [ 4 2 ] [ 3 6 5 ] ===> 2.0 + 4.666 = 6.666 [ 4 ] [ 2 3 6 5 ] ===> 0.0 + 10 = 10Result: 2.5 < 2* 2.0 Use 2.0 to approximate
Input: 4 2 3 6 5 6 12 16
Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0.0 | 0.0 | 0.5 | 2.0 | 2.0 | ?? | ?? | ?? | +----------+ +----+ +-----------+ 0.0 0.5 2.0
- And so on... - Final result:
Approximate V-optimal Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Appr Error: 0.0 | 0.0 | 0.5 | 2.0 | 2.0 | 2.0 | 13.3 | 13.3 | - Compare
the result
of Guha's algorithm and
the actual minimum error result:
Input: 4 2 3 6 5 6 12 16
V-optimal Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0.0 | 0.0 | 0.5 | 2.0 | 2.5 | 2.66 | 13.3 | 21.3 | +----------+ +----+ +------------------+ +-----------+ 0.0 0.5 2.0 13.3
- Initially:
- Step 3:
construct
approximate V-optimal histogram
with
B = 3 bucket
Important Different between Guha's Algorithm and Jagadish's V-opt. Histogram:
- Guha's algorithm will use the approximate solution in the remainder of the execution !!!
- Initially:
Input: 4 2 3 6 5 6 12 16
Histogram with 3 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0 | 0 | 0 | ?? | ?? | ?? | ?? | ?? | +---------------+ 0.0
- To find the best bucket partition
for values 4 2 3 6, we try:
{ 4 2 3 } [ 6 ] ===> MinError[2][3] + 0 { 4 2 } [ 3 6 ] ===> MinError[2][2] + (3 - 4.5)2 + (6 - 4.5)2 { 4 } [ 2 3 6 ] ===> MinError[2][1] + (2 - 3.66)2 + (3 - 3.66)2 + (6 - 3.66)2 | | +---------+ 2 bucket optimal histogram Using the result from the 2 bucket optimal histogram: { 4 2 3 } [ 6 ] ===> 0.5 + 0 = 0.5 <---- Min { 4 2 } [ 3 6 ] ===> 0.0 + 4.5 = 4.5 { 4 } [ 2 3 6 ] ===> 0.0 + 8.666 = 8.666Result: 0.5 > (1 + δ) * 0.0 ==> Start a new bucket !
Input: 4 2 3 6 5 6 12 16
Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0 | 0 | 0 | 0.5 | ?? | ?? | ?? | ?? | +-----------------+ +---+ 0.0 0.5
- To find the best bucket partition
for values 4 2 3 6 5, we try:
{ 4 2 3 6 } [ 5 ] ===> MinError[2][4] + 0 { 4 2 3 } [ 6 5 ] ===> MinError[2][3] + (6 - 5.5)2 + (5 - 5.5)2 { 4 2 } [ 3 6 5 ] ===> MinError[2][2] + (3 - 4.66)2 + (6 - 4.66)2 + (5 - 4.66)2 { 4 } [ 2 3 6 5 ] ===> MinError[2][1] + (2 - 4)2 + (3 - 4)2 + (6 - 4)2 + (5 - 4)2 | | +-----------+ 2 bucket optimal histogram Using the result from the 1 bucket optimal histogram: { 4 2 3 6 } [ 5 ] ===> 2.0 + 0 { 4 2 3 } [ 6 5 ] ===> 0.5 + 0.5 = 1.0 <--- Min { 4 2 } [ 3 6 5 ] ===> 0.0 + 4.666 = 4.666 { 4 } [ 2 3 6 5 ] ===> 0.0 + 10.0 = 10.0Result: 1.0 <= (1 + δ) * 0.5 - extend the current bucket
Input: 4 2 3 6 5 6 12 16
Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Min Error: 0 | 0 | 0 | 0.5 | 0.5 | ?? | ?? | ?? | +-----------------+ +----------+ 0.0 0.5
- And so on....
- Important property of the approximation histogram:
- The number of buckets of the approximation histogram is unknown
- To accommodate
a variable number of
buckets, we used a
linked list
to represent the histogram
- Structure of a list element:
+-----------------------+ | a (left boundary) | +-----------------------+ | b (right boundary) | +-----------------------+ | Sol (histogram value | +-----------------------+
- Example:
how to represent the
approximate solution
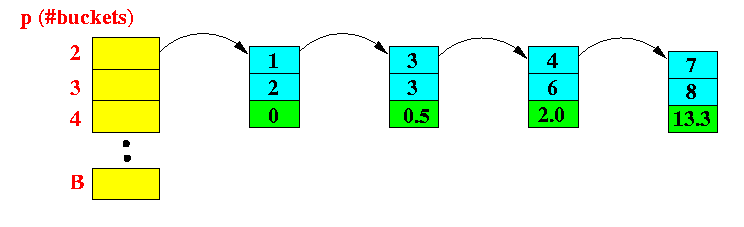
for the 2 bucket V-optimal histogram:
Approximate V-optimal Histogram with 2 bucket: Values: 1..1 | 1..2 | 1..3 | 1..4 | 1..5 | 1..6 | 1..7 | 1..8 | -------+------+------+------+------+------+------+------+--- Appr Error: 0.0 | 0.0 | 0.5 | 2.0 | 2.0 | 2.0 | 13.3 | 13.3 |is represented as follows:
- Guha's paper:
click here
- Guha has a newer paper with the algorithm on page 9,
but there are lot's of bugs in the algorithm, so
read with caution:
click here
- Algorithm:
/* ------------------------------------------------ Help function to compute Error in a bucket ------------------------------------------------ */ SqError(int a, int b) { s2 = PP[b] - PP[a]; s1 = P[b] - P[a]; return (s2 - s1*s1/(b-a+1)); } /* ---------------------------------------------- Prepare arrays to compute error efficiently ---------------------------------------------- */ P[0] = 0; PP[0] = 0; for (i = 1; i <= N; i++) { P[i] = P[i-1] + xi PP[i] = PP[i-1] + xi2 } // Note: We don't approximate OPT[1][..] // OPT[1][..] is computed exactly using SqError(a,b) /* ------------------------------------------------------------------ Now we compute the approximate V-opt. histogram with B buckets Output: BestError[i][k] = best error of histogram using k buckets on data points (1..i) ------------------------------------------------------------------ */ // The dynamic algorithm uses these variables: // // k = # buckets // i = current item - items processed are: (1..i) // Initialization /* ----------------------------------------------------- Set up (B-1) linked list Q[k] (k = 2..B) to store the approximate solution histograms Each Q[k] is a linked list of records of the form: Q[k].a = left point of bucket Q[k].b = right point of bucket Q[k].Sol = approximate solution at point Q[k].a ----------------------------------------------------- */ for (k = 2; k <= B; k++) { Q[k] -> (a = 1, b = 1, Sol = 0); // List element } for (k = 1; k <= B; k++) { // Find optimal histogram using k buckets currApprox = Q[k] -> Sol // initially equal to 0 for (i = 1; i <= N; i++) { minError = INFINITE; // Start value // Try every possible size for the last bucket for (j = 1; j <= i-1; j++) // Last bucket is [j..i] { if ( Lookup(Q[k-1], j) + SqError(j+1,i) < minError ) { minError = Lookup(Q[k-1], j) + SqError(j+1,i); // Better division found } } if ( minError > (1 + δ) * currApprox ) { Add new bucket (a = i, b = i, Sol = minError) to Q[k] } } }
- Theorem 3
of Guha's paper
states:
- The algorithm above will compute a histogram with error Sol[p+1,n+1] that is at most (1 + δ)p × OPT[p+1,n+1]
- Proof: (for you eyes only - I retraced the proof...
I will not discuss it in class...)