- Notations:
- pfi =
the ith packet
of flow f
- A(pfi) =
the arrival time of the
ith packet
of flow f
- L(pfi) =
the departure (leave) time of the
ith packet
of flow f
- len(pfi)
(also:
lfi) =
the length (#bytes) of the
the ith packet
of flow f
- rf =
the reserved rate (weight)
of flow f
- VT(t) =
the system virtual clock (time)
at real time t
Recall that:
- The system virtual time (clock)
is equal to the
left time value of
the current bin:
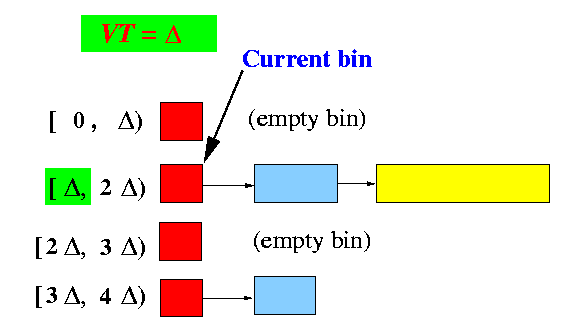
- The system virtual time (clock)
is equal to the
left time value of
the current bin:
- Two important times:
-
VT(A(pfi)) =
the system virtual clock (time)
at the moment
when packet
pfi
arrives
- VT(L(pfi)) = the system virtual clock (time) at the moment when packet pfi leaves
-
VT(A(pfi)) =
the system virtual clock (time)
at the moment
when packet
pfi
arrives
- V(pfi) =
the virtual time stamp of the
ith packet
of flow f
Recall that:
- V(pfj) = max( VT(A(pfj)), V(pfj−1) ) + len(pfj)/rf
- pfi =
the ith packet
of flow f
- Fairness definition of Golestani:
(See: click here )
- A scheduling algorithm is fair if:
if f and g are continuously backlogged in [t1,t2], then: ∃ constant c: | wf(t1,t2) - wg(t1,t2) | < c i.e.: | Wf(t1,t2) Wg(t1,t2) | ∃ constant c: | --------- - --------- | < c | rf rg |
- A scheduling algorithm is fair if:
- We will show the
difference in
normalized service received
using the BSFQ scheduler
by 2 different backlogged flows
is bounded:
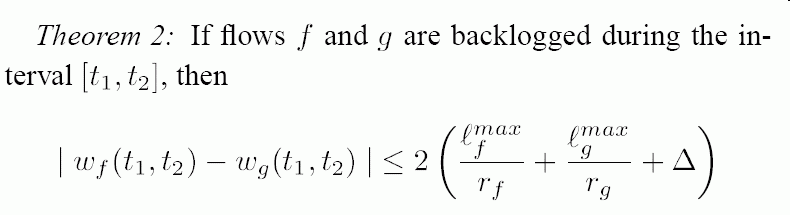
- But before we can do so,
we need to
prove some
preliminary facts....
- V(pfi) =
the (virtual) time stamp of
packet
pfi
- Packet
pfi
is inserted into some
time bin [xΔ, (x+1)Δ):
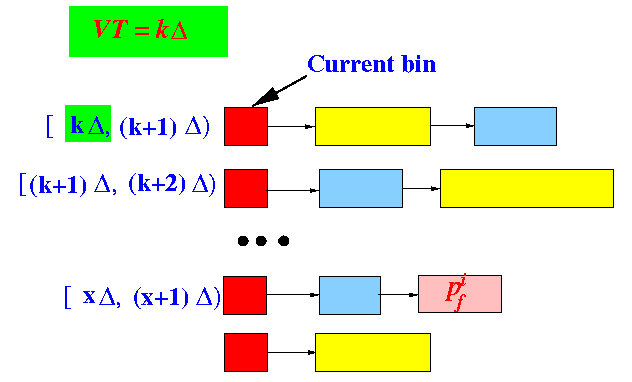
- Because packet
pfi
is in
time bin [xΔ, (x+1)Δ),
we conclude that:
xΔ ≤ V(pfi) < (x+1)Δ ........ (1)
- When the packet
pfi is
about to
leave the
BSFQ server, the
current bin
must be
time bin [xΔ, (x+1)Δ):
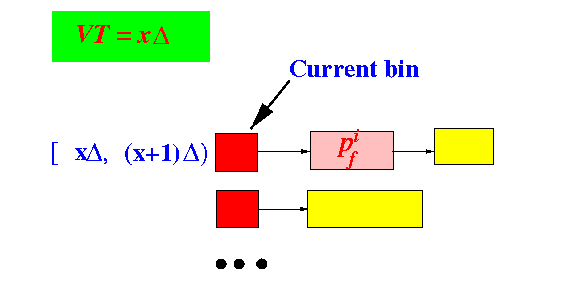
- The virtual time
at the moment that
packet
pfi
departs is equal to:
VT( L(pfi) ) = x Δ ...... (2)
- Therefore:
xΔ ≤ V(pfi) < (x+1)Δ ...... (1) VT( L(pfi) ) = x Δ ...... (2)
==> VT( L(pfi) ) ≤ V(pfi) < VT( L(pfi) ) + Δ ...... (3)
- When a flow f is
backlogged,
the time stamp
V(pfi)
of packet
pfi is
equal to:
len(pfi) V(pfi) = V(pfi-1) + -------- ........ (4) rk - Proof:
- If flow f is
backlogged, then:
- Packet pfi arrives before its predecessor packet pfi-1 leaves
- Therefore:
- A(pfi) < L(pfi-1)
- The virtual time function
VT(t) of BSFQ is
a monotonic increasing
(step) function:
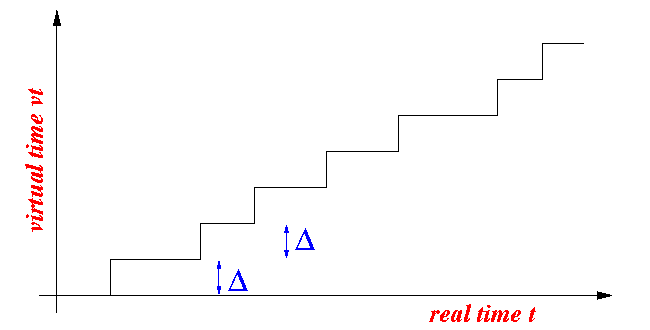
(I.e., the function values never decreases)
Property of a monotonic increasing function:
- If t1 ≤ t2, then: VT(t1) ≤ VT(t2)
- Therefore:
- Because A(pfi)
<
L(pfi-1)
, we have that:
- VT( A(pfi) ) < VT( L(pfi-1) ) .......... (5)
Therefore:
VT( A(pfi) ) < VT( L(pfi-1) ) ......... (5)VT( L(pfi) ) ≤ V(pfi) < VT( L(pfi) ) + Δ ...... (3)
Applied to packet pfi-1: VT( L(pfi-1) ) ≤ V(pfi-1) < VT( L(pfi-1) ) + Δ ...... (3a)
- Because A(pfi)
<
L(pfi-1)
, we have that:
- Therefore:
len(pfi) V(pfi) = max ( VT( A(pfi) ) , V(pfi-1) ) + --------- (use 5A) rf len(pfi) = V(pfi-1) + --------- (Q.E.D.) rf
- If flow f is
backlogged, then:
- Theorem 2:
- If flows
f and
g are
backlogged during
time interval
[t1, t2],
then:
+- -+ | | | lenfmax lenfmax | | wg(t1, t2) - wg(t1, t2) | ≤ 2 × | ------ + ------ + Δ | | | | rf rg | +- -+Where:
- lenfmax = max packet length of packets of flow f
- lengmax = max packet length of packets of flow g
- If flows
f and
g are
backlogged during
time interval
[t1, t2],
then:
- Proof:
- The service
Wf(t1, t2)
to flow f
in interval
[t1, t2]
is given by the
shaded area:

- A lower bound for the
service
Wf(t1, t2) is:
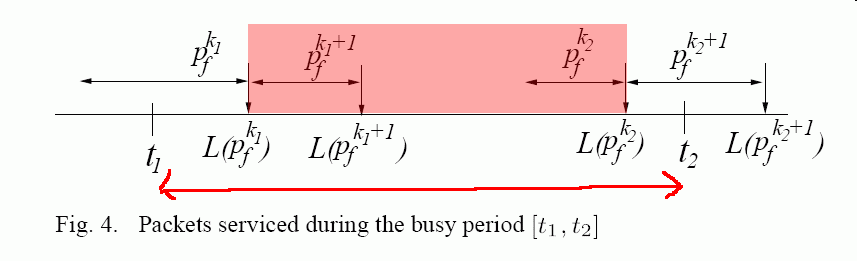
I.e.:
Wf(t1, t2) ≥ len(pfk1+1) + .... + len(pfk2)
len(pfk1+1) + .... + len(pfk2) <==> wf(t1, t2) ≥ ------------------------------- .......... (6) rf
- An upper bound for the
service
Wf(t1, t2) is:
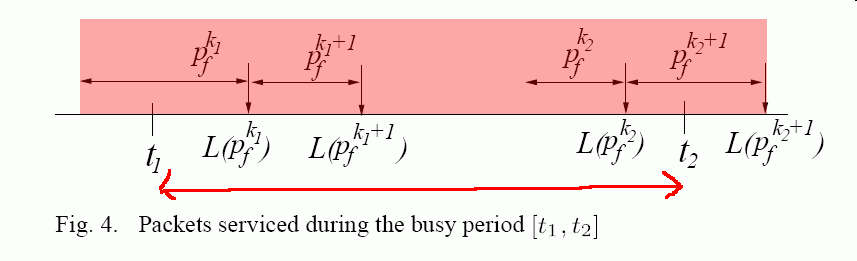
I.e.:
Wf(t1, t2) ≤ len(pfk1) + .... + len(pfk2+1)
len(pfk1) + .... + len(pfk2+1) <==> wf(t1, t2) ≤ ------------------------------- .......... (7) rf
- We will first find an
upper bound on
wf(t1, t2)
:
- From the timing in this figure:
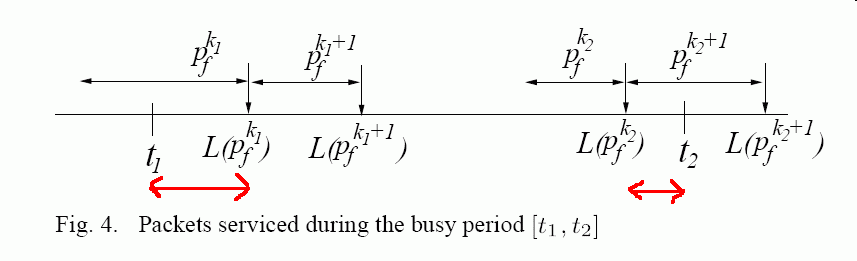
and the fact that VT(t) is non-decreasing, we have that:
VT(t1) ≤ V( L(pfk1) ) and: VT(t2) ≥ V( L(pfk2) )Therefore:
VT(t2) - VT(t1) ≥ V( L(pfk2) ) - V( L(pfk1) ) ....... (8)
Using Equation (3): (click here)
VT( L(pfi) ) ≤ V(pfi) < VT( L(pfi) ) + Δ ...... (3)
We have: V(pfk2) < VT( L(pfk2) ) + Δ <==> VT( L(pfk2) ) > V(pfk2) - Δ and: VT( L(pfk1) ) ≤ V(pfk1)Apply the result to Equation (8):
VT(t2) - VT(t1) ≥ V( L(pfk2) ) - V( L(pfk1) ) ....... (8) ≥ [V(pfk2) - Δ] - V(pfk1) = V(pfk2) - V(pfk1) - Δ ....... (9)
- Because flow f is
backlogged during
interval
[t1, t2], we have:
len(pfk2) V(pfk2) = V(pfk2-1) + ------------ rf len(pfk2-1) V(pfk2-1) = V(pfk2-2) + ------------ rf .... len(pfk1+1) V(pfk1+1) = V(pfk1) + ------------ rf
Therefore: [V(pfk2) - V(pfk2-1)] + [V(pfk2-1) - V(pfk2-2)] + ... + [V(pfk1+1) - V(pfk1)] len(pfk1+1) + ... + len(pfk2) = ----------------------------- rf len(pfk1+1) + ... + len(pfk2) <==> V(pfk2) - V(pfk1) = ------------------------------- rf
- Apply the result to
Equation (9):
VT(t2) - VT(t1) ≥ V(pfk2) - V(pfk1) - Δ ....... (9) len(pfk1+1) + ... + len(pfk2) = ------------------------------- - Δ rf
len(pfk1+1) + ... + len(pfk2) <==> ------------------------------- ≤ VT(t2) - VT(t1) + Δ rf
- Apply the result to
Equation (7) and
we can finally formulate
an upperbound for
wf(t1, t2)
:
len(pfk1) + .... + len(pfk2+1) wf(t1, t2) ≤ ------------------------------- .......... (7) rf len(pfk1) + len(pfk1+1) + .... + len(pfk2) + len(pfk2+1) = ---------------------------------------------------- rf len(pfk1) len(pfk2+1) = VT(t2) - VT(t1) + Δ + --------- + ----------- rf rf
Or: len(pfmax) wf(t1, t2) ≤ VT(t2) - VT(t1) + 2 --------- + Δ ..... (10) rf
- From the timing in this figure:
- A lower bound for
wf(t1, t2)
:
- From the timing relationship:
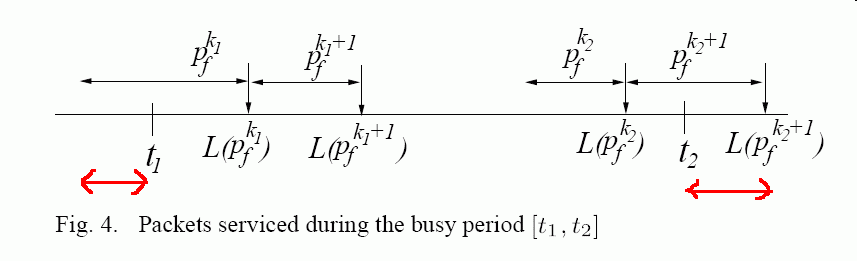
and the fact that VT(t) is non-decreasing, we have:
V( Lpfk1-1) ) ≤ V(t1) and: V(t2) ≤ V( Lpfk2+1) )Therefore:
V(t2) - V(t1) ≤ V( Lpfk2+1) ) - V( Lpfk1-1) ) ........ (10)
Using Equation (3): (click here)
VT( L(pfi) ) ≤ V(pfi) < VT( L(pfi) ) + Δ ...... (3)
We have: VT( L(pfk2+1) ) ≤ V(pfk2+1) and: V(pfk1-1) < VT( L(pfk1-1) ) + Δ <==> VT( L(pfk1-1) ) > V(pfk1-1) - ΔApply the result to Equation (10):
VT(t2) - VT(t1) < V( L(pfk2+1) ) - V( L(pfk1-1) ) ....... (10) < V(pfk2+1) - [V(pfk1-1) - Δ] = V(pfk2+1) - V(pfk1-1) + Δ ....... (11)
- Because flow f is
backlogged during
interval
[t1, t2]:

we have:
len(pfk2+1) V(pfk2+1) = V(pfk2) + ------------ rf len(pfk2) V(pfk2) = V(pfk2-1) + ------------ rf .... len(pfk1+1) V(pfk1+1) = V(pfk1) + ------------ rf But: len(pfk1) V(pfk1) = max( VT(A(pfk1)), V(pfk1-1) ) + ------------ rf
Therefore: [V(pfk2+1) - V(pfk2)] + [V(pfk2) - V(pfk2-1)] + ... + [V(pfk1+1) - V(pfk1)] len(pfk1) + ... + len(pfk2+1) = ----------------------------- rf len(pfk1) + ... + len(pfk2+1) <==> V(pfk2+1) - V(pfk1) = ------------------------------- ....... (12) rf
- From the timing relationship:
- We must consider 2 cases to
complete the proof:
- V(pfk1-1) ≥ VT(A(pfk1))
- V(pfk1-1) < VT(A(pfk1))
Case 1: V(pfk1-1) ≥ VT(A(pfk1))
- Then we have:
len(pfk1) V(pfk1) = V(pfk1-1) + ------------ rf
- Apply the result to
Equation (11):
VT(t2) - VT(t1) ≤ V(pfk2+1) - V(pfk1-1) + Δ ....... (11) = V(pfk2+1) - V(pfk1-1) + V(pfk1) - V(pfk1) + Δ = [V(pfk2+1) - V(pfk1)] + [V(pfk1) - V(pfk1-1)] + Δlen(pfk1+1) + ... + len(pfk2+1) V(pfk2+1) - V(pfk1) = ------------------------------- ....... (12) rflen(pfk1) V(pfk1) = V(pfk1-1) + ------------ rf
- Apply the result to
Equation (6) and
we can finally give an
lower bound for
Case 1:
len(pfk1+1) + .... + len(pfk2) wf(t1, t2) ≥ ------------------------------- .......... (6) rf len(pfk1) + .... + len(pfk2+1) len(pfk1) len(pfk2+1) = ------------------------------- - ---------- - ---------- rf rf rfUse Equation (13)
Case 2 is similar, so I will spare you the proof :-)
- The proof is completed as follows:
- We have found a lower bound
and an upper bound for
wf(t1, t2)
:
len(pfmax) len(pfmax) VT(t2) - VT(t1) - 2 ---------- - Δ ≤ wf(t1, t2) ≤ VT(t2) - VT(t1) + 2 ---------- + Δ rf rf - The lower bound
and an upper bound for
wg(t1, t2)
of flow g is then:
len(pgmax) len(pgmax) VT(t2) - VT(t1) - 2 ---------- - Δ ≤ wg(t1, t2) ≤ VT(t2) - VT(t1) + 2 ---------- + Δ rg rg
- Therefore:
len(pfmax) len(pgmax) wf(t1, t2) - wg(t1, t2) ≤ 2 ---------- + Δ + 2 ---------- + Δ rf rg and: len(pgmax) len(pfmax) wg(t1, t2) - wf(t1, t2) ≤ 2 ---------- + Δ + 2 ---------- + Δ rg rfThus:
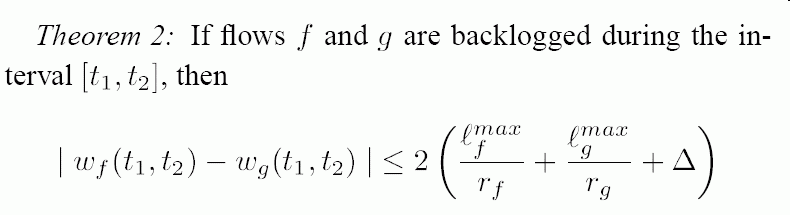
- We have found a lower bound
and an upper bound for
wf(t1, t2)
:
- The service
Wf(t1, t2)
to flow f
in interval
[t1, t2]
is given by the
shaded area: