---

A more practical definition of fairness

---

• Practical situation...
  • Max-min fairness:

    Is a static definition

    ---

  • Network connections:

    are some times idle            some times active Are established and disconnected

    ---

  • Bottom line:

    max-min fairness is difficult to enforce on network connections....

    We need a more practical (easily enforceable) definition of fairness....

  ---

  ---

  ---

  ---

• Definition: Active flows
  • Active Flows:

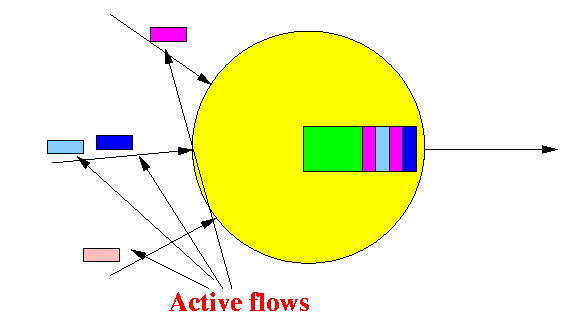
    Note:

    A flow (connection) is active if it is sending packets to a router An active flow may not have packets buffered at the router due to temporal inactivity Example: There are 4 active flows But... the flow at the bottom of the figure does not have packets buffered

  ---

  ---

• Definition: Backlogged flows
  • Backlogged Flows:

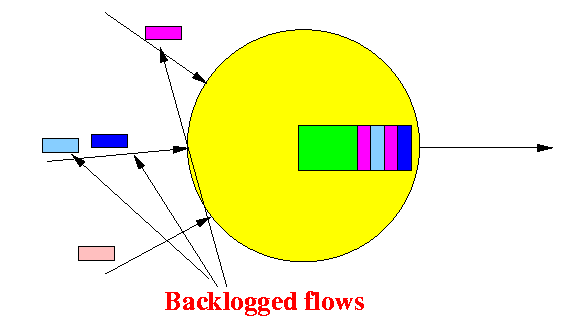
    Note:

    A flow (connection) is backlogged if it has packets buffered at a router

  ---

  ---

  ---

  ---

• Definition: service (work) for a flow f
  • Work for flow f:

    Wf (t1, t2) = work performed for a flow f during the time interval [ t1, t2 ]   This is the amount of data of flow f transmitted in the interval [ t1, t2 ]

  • Fact:

    Active flows (but not backlogged) that has no packets in the buffer of the router will not receive any service Only backlogged flows will receive service from the router !

  ---

  ---

• A more practical "Fairness" definition
  • Degree of unfairness: Difference in the received service between backlogged flows:

    Work received by a flow f in interval [t1, t2]:           Wf (t1, t2)             Work received by a flow g in interval [t1, t2]: Wg (t1, t2)              Degree of unfairness = difference in received service --- i.e., work received: | Wf (t1, t2) − Wg (t1, t2) |

    ---

  • Manifestation of unfairness:

    A method that is fair will does not favor any particular flow.... A method that is unfair will does favor some flow over another flow.... Manifestation of "flavoring a flow": When a method flavors a flow x, then the flow x will receive more service So when a method flavors a flow f over a flow g then: | Wf (t1, t2) − Wg (t1, t2) | will increase when the interval [t1, t2] increases In other words: If a method is unfair, the difference in the received service between two flows will become arbitrarily large when given sufficient time (for the unfair method to operate)

    ---

    ---

  • A practical definition of "fairness"...

    A transmission method is fair if: | Wf (t1, t2) − Wg (t1, t2) |   ≤   some specific constant            for every interval [t1, t2] where both flows f and g are backlogged

    ---

  • Note:

    This definition of fairness allows us to prove mathematically that some packet transmission (scheduling) method is fair We will see some proof in the discussion of the methods...

  ---

  ---

  ---

  ---

• Weighted fairness
  • Weights and reservations:

    The fairness definition above can be generalized to given flows different weights Traditionally, weights corresponds to (bandwidth) reservations for flows

  ---

  ---

• Definition: Reservation of flow f
  • Reservation r_f:

    The reservation rf of flow f is the amount of transmission capacity (bandwidth) reserved for flow f

    ---

  • Note:

    If a link has a transmission capacity C (i.e., C bits per second transmission rate), then the reservation cannot exceed C In fact, the total reservation must be not exceed the link transmission capacity C: ∑all flows f   rf   ≤  C

    ---

    ---

  • Bandwidth unit:

    Some literature uses the link capacity C as unit measure for bandwidth            (I.e., a reservation of 1 means reserve all capacity on the link) In these papers, the reservation rf  is then: rf   ≤ 1         and, ∑all flows f   rf   ≤  1

  ---

  ---

  ---

  ---

• Definition: normalized service (work) for a flow f
  • Normalized service for flow f:

    The normalized service performed for a flow f during the time interval [ t1, t1 ]   ( wf (t1, t1) ) is defined as: Wf(t1,t1) wf(t1,t1) = ---------- ...... (1) rf

    ---

  • Significance (meaning) of the normalized service:

    rf = the amount of reservation of flow f I.e.: rf = the amount of work that flow f is entitled to Wf = the actual amount of work received by flow f Ideally: Wf(t1,t1) wf(t1,t1) = ---------- = 1 (or very close to 1) rf for every flow f

  ---

  ---

• Definition: Fair service for different flows f and g
  • Fair service:

    A packet scheduling method is fair if the difference in the normalized service provided to any two flows that are continuously backlogged over any interval [t1,t2] is bounded by some constant.

    ---

  • In Mathematical terms:

    A scheduling algorithm is fair if: if f and g are continuously backlogged in [t1,t2], then: ∃ constant c: | wf(t1,t2) - wg(t1,t2) | < c i.e.: | Wf(t1,t2) Wg(t1,t2) | ∃ constant c: | --------- - --------- | < c | rf rg | (This fairness definition was introduced by S. J. Golestani and it is the generally accepted fairness criteria for long-running network connections)

    ---

    ---

  • Notes:

    The smaller the constant c, the smaller the difference in the obtained (normalized) service between 2 flows. I.e.: The smaller the constant c, the more fair the scheduling algorithm is.... If the constant c = 0, then the scheduling algorithm is perfectly fair !!!