- Purpose of queueing models:
- Analysis of queueing models can provide answers to performance related questions through mathematical analysis
- Common performance measures:
- Average queue length N
This is the average number of customers in the system.
(Better: This is the average number of customers waiting in the system to get service....)
- Average delay time T
The delay is defined as:
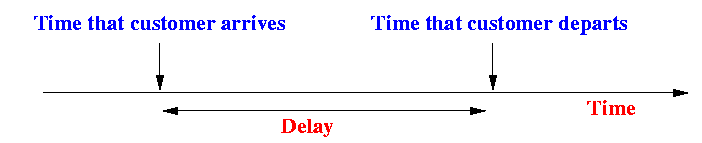
The average delay time is the average amount of time that a customer spends in the system.
- Average queue length N
- Consider the following simple example:
- 50% of the time, the system is empty
- 50% of the time, the
system has 1 customer
- Then the average number of customers
in the system is the
weighted sum:
N = 0.5 × 0 + 0.5 × 1 = 0.5
- In general,
the average queue length
(or the average number of customers
in system) is equal to:
N = mean (expected) number of customer = 0 × Ҏ[ k customers in system] + 1 × Ҏ[ 1 customer in system] + 2 × Ҏ[ 2 customers in system] + .... = ∑ {k = 0, 1, .., ∞} k × Ҏ[ k customers in system] (definition of "expected value") = ∑ {k = 0, 1, .., ∞} k × pk ........ (1)
- Recall that
the state probability i
of the M/M/1 queue is
Ҏ[ k customers in system] = ρk (1 - ρ) (see: click here)
The average (expected) queue length N of the M/M/1 queue is:
N = ∑ {k = 0, 1, .., ∞} k × pk (definition of N) = ∑ {k = 0, 1, .., ∞} k × ρk (1 - ρ) = (1 - ρ) × ∑ {k = 0, 1, .., ∞} k × ρk .... (2)U = ∑ {k = 0, 1, .., ∞} ρk = 1/(1 - ρ) (see: click here) Or: U = ∑ {k = 0, 1, .., ∞} ρk = (1 - ρ)-1
Thus: dU ---- = ∑ {k = 0, 1, .., ∞} k ρk-1 = (1 - ρ)-2 dρ Therefore: ∑ {k = 0, 1, .., ∞} k ρk = ρ × (1 - ρ)-2 ......... (3)
Substitute (3) in (2): N = (1 - ρ) × ∑ {k = 0, 1, .., ∞} k × ρk ..... (2) [repeated] = (1 - ρ) × ρ × (1 - ρ)-2 = ρ × (1 - ρ)-1
Therefore, the mean number of customers in an M/M/1 queue is equal to:ρ N(M/M/1) = ------- ..... (4) 1 - ρ