- Definition:
- A birth/death Markov process
is a Markov process where:
pi,i+1 = bi (birth) pi,i-1 = di (death) pi,i = 1 - bi - di pi,k = 0 for k ≤ i-2 or k ≥ i+2
- A birth/death Markov process
is a Markov process where:
- The transition diagram
of a birth/death process looks
like this:

In other words:
- The possible events in a
birth/death Markov provess are:
- Exactly one birth
- Exactly one death
(The event that there is no birth and no death is the case that no event occurs)
- The possible events in a
birth/death Markov provess are:
- Definitions:
- A birth = an arrival (of a client) into the system
- death = a departure (of a client) from the system
- Poisson birth/death process:
- Ҏ[ an arrival occurs in time interval Δt ] = λ × Δt
-
Ҏ[
a departure
occurs in time interval Δt
] =
μ × Δt
- λ = arrival rate (see: click here )
- μ = departure rate
- State transition diagram for a Poisson birth/death process:
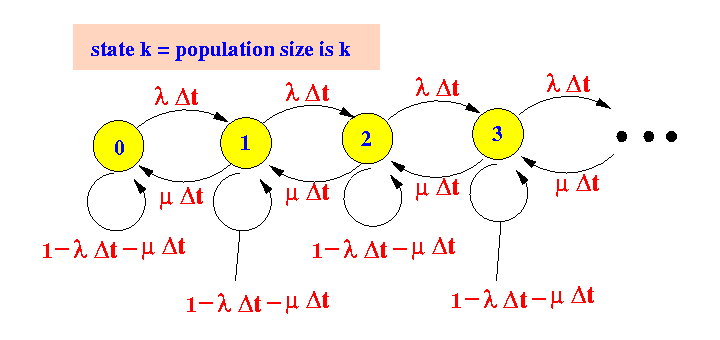
Resulting state equations:
p0 = p0 (1 - λΔt) + p1 μΔt p1 = p0 λΔt + p1 (1 - λΔt - μΔt) + p2 μΔt p2 = p1 λΔt + p2 (1 - λΔt - μΔt) + p3 μΔt p3 = p2 λΔt + p3 (1 - λΔt - μΔt) + p4 μΔt ...
Or: p0 λΔt = p1 μΔt p1(λΔt + μΔt) = p0 λΔt + p2 μΔt p2(λΔt + μΔt) = p1 λΔt + p3 μΔt p3(λΔt + μΔt) = p2 λΔt + p4 μΔt ...
Or: p0 λ = p1 μ p1(λ + μ) = p0 λ + p2 μ p2(λ + μ) = p1 λ + p3 μ p3(λ + μ) = p2 λ + p4 μ ...
Or: p0 λ = p1 μ p1 λ + p1 μ = p0 λ + p2 μ p2 λ + p2 μ = p1 λ + p3 μ p3 λ + p3 μ = p2 λ + p4 μ ...
Or: p0 λ = p1 μ p1 λ = p2 μ p2 λ + p2 μ = p1 λ + p3 μ p3 λ + p3 μ = p2 λ + p4 μ ...
Or: p0 λ = p1 μ p1 λ = p2 μ p2 λ = p3 μ p3 λ + p3 μ = p2 λ + p4 μ ...And so on....
Final set of equations:
p0 λ = p1 μ p1 λ = p2 μ p2 λ = p3 μ p3 λ = p4 μ ...
Or: p1 = λ/μ × p0 p2 = λ/μ × p1 p3 = λ/μ × p2 p4 = λ/μ × p3 ...
Or: p1 = λ/μ × p0 .... (1) p2 = (λ/μ)2 × p0 .... (2) p3 = (λ/μ)3 × p0 .... (3) p4 = (λ/μ)4 × p0 .... (4) ...We can express every pi, i = 1, 2, 3, ... in terms on p0
Unfortunately, we do not (yet) know the value of p0...
- We need one more equation to
solve this system, which is:
p0 + p1 + p2 + p3 + ... = 1 .... (5)
Substituting pi in equation (5) and we get:
p0 + (λ/μ)1 × p0 + (λ/μ)2 × p0 + (λ/μ)3 × p0 + .... = 1
p0 × ( 1 + (λ/μ)1 + (λ/μ)2 + (λ/μ)3 + .... ) = 1S = 1 + x1 + x2 + x3 + x4 + ... xS = x1 + x2 + x3 + x4 + ... - ------ ------------------------------------ (1-x)S = 1 Therefore: 1 1 + x1 + x2 + x3 + x4 + ... = ------- 1 - x
1 p0 × ------- = 1 1-(λ/μ)
p0 = 1 - (λ/μ) = 1 - ρ ...... (6)Notation:
- ρ = λ/μ
- Steady state probability distribution of a Poisson birth/death
process with arrival rate λ and departure rate μ:
p0 = (λ/μ)0 × (1-(λ/μ)) p1 = (λ/μ)1 × (1-(λ/μ)) p2 = (λ/μ)2 × (1-(λ/μ)) p3 = (λ/μ)3 × (1-(λ/μ)) ....
Or: p0 = ρ0 × (1 - ρ) p1 = ρ1 × (1 - ρ) p2 = ρ2 × (1 - ρ) p3 = ρ3 × (1 - ρ) .... Or:Ҏ[ k customers in system ] = pk = ρk × (1 - ρ)
- A popular method for finding the
equilibrium (steady state) probability
distribution of a Markov chain is
using rate transition diagrams
- Rate transition diagram:
- A rate transition diagram is obtained by removing the transitions that goes from a state into the same state from a state transition diagram
- Example:
- State transition diagram:
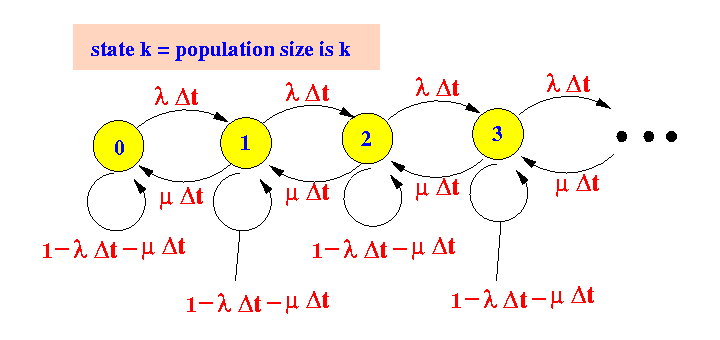
- State diagram without loops to itself:
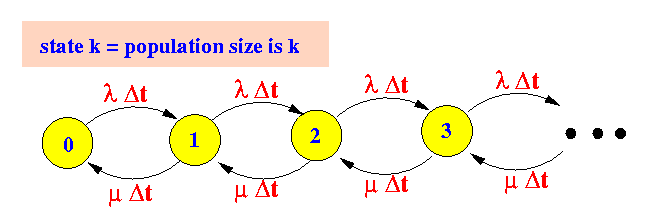
After normalization by dividing by Δt:

- State transition diagram:
- Note:
- λ = arrival rate of clients
- μ =
departure rate of
clients
- The weights on the
arcs in the
digram are
the rates of
arrival and
departure
Hence the name: rate transition diagram
- Algorithm:
- Find a cut in the
Markov chain that
divide the Markov chain into
2 disjoint pieces
- In the equilibrium state,
the number of transitions
from one side
the cut to the other side
must be equal
to the reverse direction
Example:
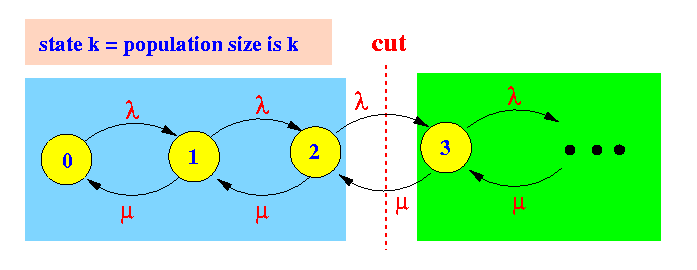
Equilibrium equation:
Flow from left to right: p2 × λ Flow from left to right: p3 × μ Equilibrium: p2 × λ = p3 × μ
- Find a cut in the
Markov chain that
divide the Markov chain into
2 disjoint pieces
- Complete example: equalibrium equations for the M/M/1 queing system
- Cut 1:
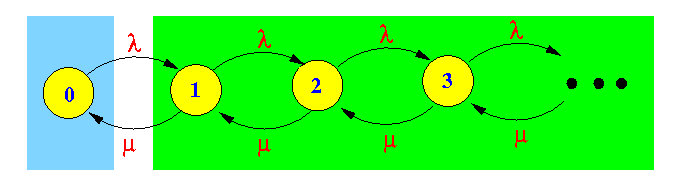
Equilibrium equation:
Flow from left to right: λ × p0 Flow from right to left: μ × p1 Equilibrium: λ × p0 = μ × p1
- Cut 2:
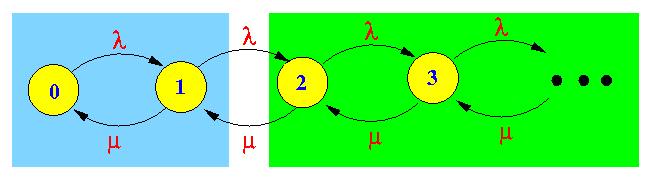
Equilibrium equation:
Flow from left to right: λ × p1 Flow from right to left: μ × p2 Equilibrium: λ × p1 = μ × p2
- And so on....
- Cut 1:
- Resulting set of equation for the equilibrium state:
p0 λ = p1 μ p1 λ = p2 μ p2 λ = p3 μ p3 λ = p4 μ ...
This is the same set of equation as before... (see: click here)