- Before we can
understand the
performance analysis of
the 802.11 protocol, we must
first understand
the sequence of events
in transmitting a packet
in 802.11
- How a termial transmits a packet:
- Recall that
we assumed that a
station always has
a packet to transmit...
Therefore, the channel is never idle
- Hence, when a station attempts the initial transmission of the next packet, it will pick a random (back-off) number x - See: click here
- Initial count down"
- The initial transmission attempt
will start counting down
from the (random) number x
as follows:
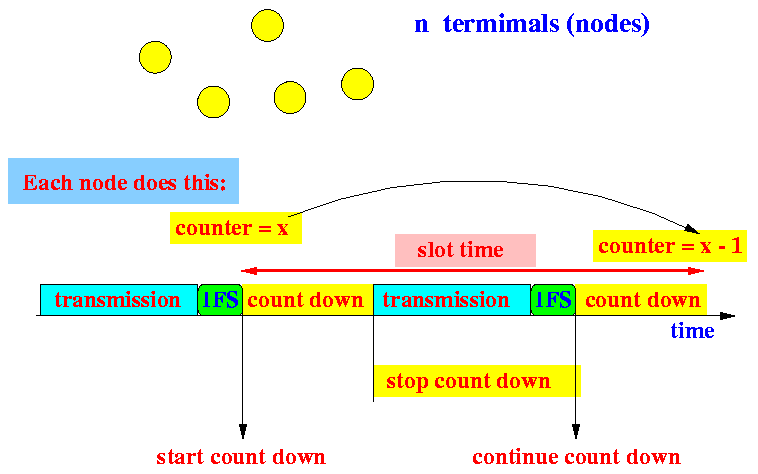
Notes:
- First the station
waits until the
channel is idle
- Then the station
waits another
IFS time
before
starting the
count down process
- The count down process
is stopped (interrupted)
when the channel is busy
- The count down process is
resumed after
IFS time
after the channel
becomes idle
Slot time = the time it takes to decrement the count down counter by one (1)
Note:
- The slot time is a random variable !!!
- The initial transmission attempt
will start counting down
from the (random) number x
as follows:
- Transmitting a packet:
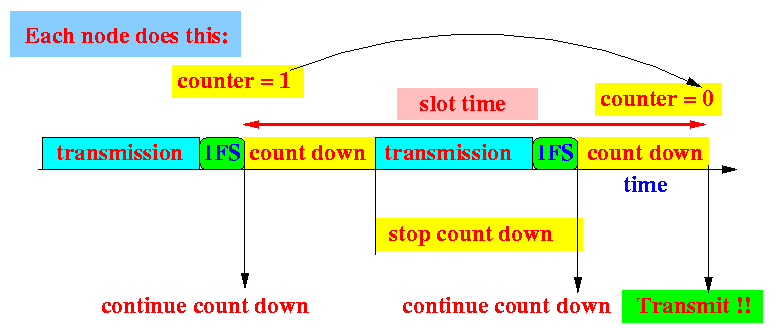
Notes:
- When the counter
become zero (0),
a station will
transmit immediately
- Note:
- The transmission can be corrupted due to a collision (another station also starts a transmission)
- When the counter
become zero (0),
a station will
transmit immediately
- Recall that
we assumed that a
station always has
a packet to transmit...
- Notations:
- n =
number of stations (nodes)
(We assume that n is fixed (unchanging) - i.e., stations do not leave or join the wireless network)
- CWmin =
the minimum threshold of
the collision window
- For less busy system, a small CWmin value (e.g., 31) will achieve good performance
- For very busy system,
a
large CWmin value (e.g., 1023)
must be used to achieve good performance
- For more details, read page 2 of the paper: click here
Wi = 2i × CWmin
- [0, Wi − 1] is the range of collision window for stage i
-
The initial transmission uses
i = 0
- Stages of the 802.11 transmission attempts:
- In stage 0, the back off counter is a random number chosen from range [0, CWmin-1]
- In stage 1, the back off counter is a random number chosen from range [0, 2×CWmin-1]
- In stage 2, the back off counter is a random number chosen from range [0, 22×CWmin-1]
- ...
- In stage m, the back off counter is a random number chosen from range [0, 2m×CWmin-1]
- In stage m+1, the back off counter is a random number chosen from range [0, 2m×CWmin-1]
- And so on...
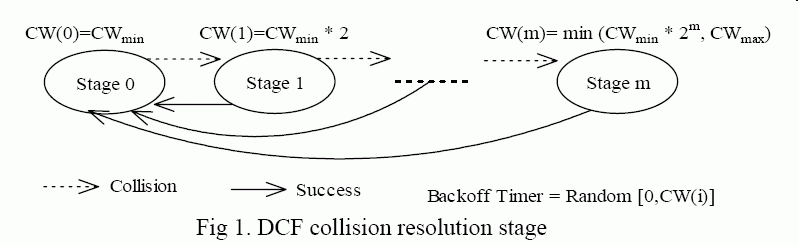
CWmax = 2m × CWmin
- m is the maximum threshold of the collision stages
- Collision stages k > m will uses the range [0, 2m × CWmin-1]
- b(t) =
the stochastic process representing the
back off time counter of
a station
- b(t) is
initially set to a
random number between
[0, Wi-1]
- b(t) is
decremented in
one slot time
- The time unit used in the
analysis is
a slot time
(Consequently: b(t+1) = b(t) − 1)
- b(t) is
initially set to a
random number between
[0, Wi-1]
- s(t) =
the stochastic process
representing the
back off stage
of a station
- After a
successful transmission
(i.e., received ACK for packet),
the value of s(t)
is re-initialized to
0
- For each unsuccessful transmission, the value of s(t) is incremented by 1
- After a
successful transmission
(i.e., received ACK for packet),
the value of s(t)
is re-initialized to
0
- n =
number of stations (nodes)
- Key assumption:
- In Each (re-)transmission attempt, the probability of collision is constant and independent
- Definition: collision probability
- p = the probability that a transmission packet involves in a collision
- State of the Markov chain at time t:
- State (s(t), b(t)) =
the station is in
back-off stage s(t) with
a back-off counter value b(t)
- s(t) = the stage at time t
- b(t) = the back-off counter value at time t
- State (s(t), b(t)) =
the station is in
back-off stage s(t) with
a back-off counter value b(t)
- Example 1: at the initial transmission, the station picks x = 1
- This state is represented by (s(t)=0, b(t)=1) or (0,1)
- Example 2: after one (1) slot time
(back-off counter is
decremented by 1)

Note:
- Since the count down counter is equal to 0, the station will transmits the packet immediately
- Example 3: the transmission collided and station picked
another random number (say: 2)
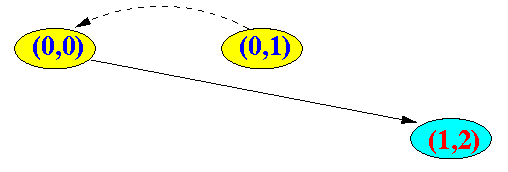
Note:
- The stage of the state is incremented to one (1) because the transmission was unsuccessful
- Example 4: after one (1) slot time
(back-off counter is
decremented by 1)
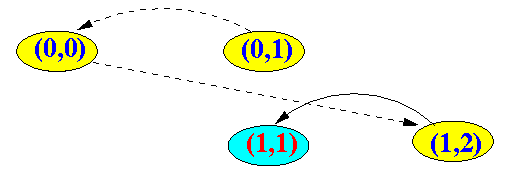
- Example 5: after one (1) slot time
(back-off counter is
decremented by 1)
Note:
- Since the count down counter
is equal to 0,
the station will
transmits the packet immediately
If unsuccessful, the next state will be (2, x) (where x is a random number)
Now, let's look at the next state when the transmission is successful
- Since the count down counter
is equal to 0,
the station will
transmits the packet immediately
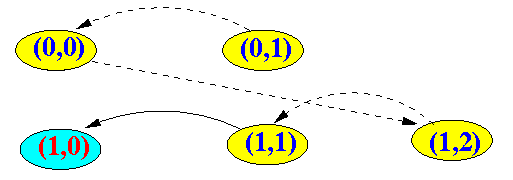
- Example 6: transmission successful.
Station
schedules next packet
and picks the random number 0
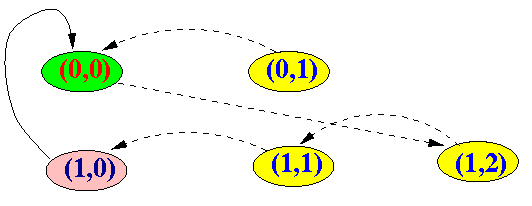
And so on !!!
- Transition probabilities:
Ҏ{ ii, k1 | i0, k0 } = Ҏ { s(t+1)=ii, b(t+1)=k1 | s(t)=i0, b(t)=k0 } = the transition probability from state (i0, k0) to state (i1, k1)
- Steady state probabilities:
bi,k = limt→∞ Ҏ{ s(t)=i, b(t)=k } = the steady state probability that the system is in state (i0, k0)Note:
- The steady state probability pi,k is the probability that we would find the system in state (i,k)
- The complete Markov chain:
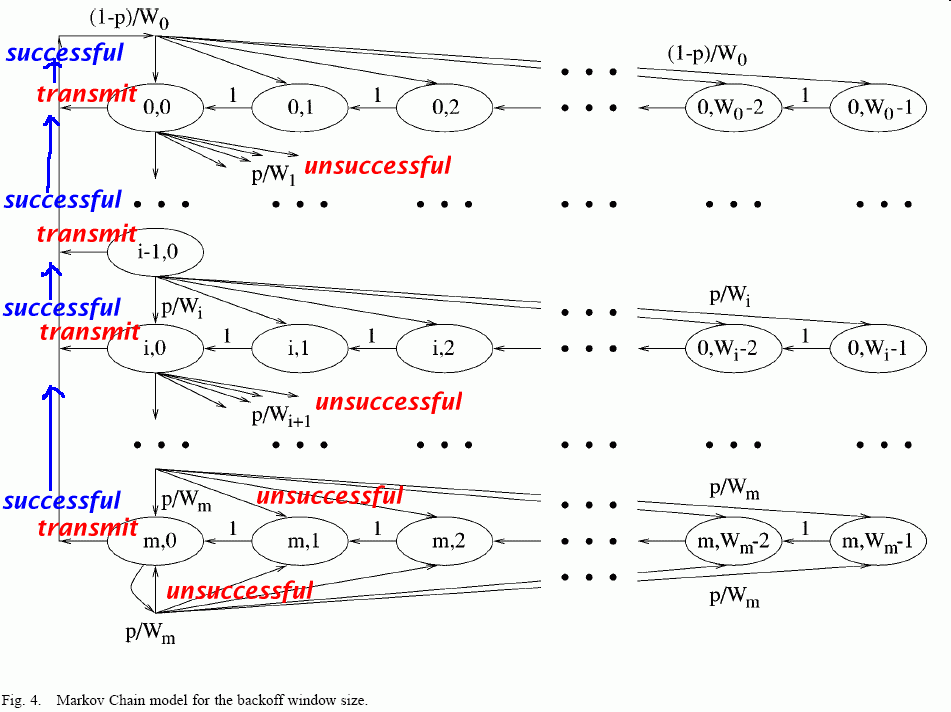
Notes:
- From the state (i, j) where
j ≥ 1,
the next state is
always (i, j−1):
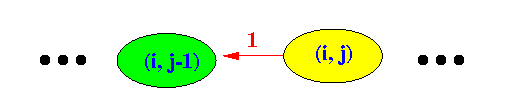
(Because the station is counting down to 0 before it will transmit.)
Therefore, the transition probability Ҏ{ i, j−1 | i, j } from state (i, j) to state (i, j−1) is equal to:
- Ҏ{ i, j−1 | i, j } = 1 ....... (1)
- When the station is in the state
(i, 0),
it will
transmit a packet immediately
The packet transmission can be:
- unsuccessful (collision) - happens with probability p
- successful - happens with probability (1−p)
Possible state transitions from the state (i, 0):
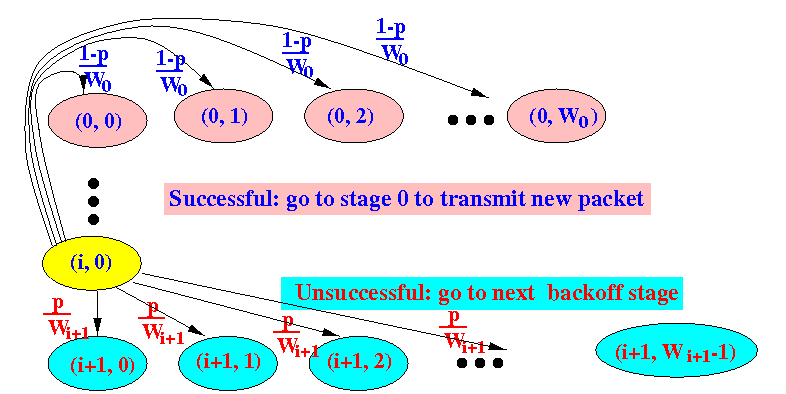
- When a transmission in
state (i,0)
is unsuccessful, the system will
go to the next stage i+1
(except at stage m) and
pick a random number
uniformly from
[0, Wi+1)
The probability that some number k ∈ [0, Wi+1) is picked is equal to 1/Wi+1
Therefore, the transition probability Ҏ{ i+1, k | i, 0 } from the state (i, 0) (i ≠ m) to the state (i+1, k) is:
1 Ҏ{ i+1, k | i,0 } = ---- × p (for i ≠ m and k = 0, 1, ..., Wi+1-1) ...... (2) Wi+1
- The stage m
is special because
there is no stage (m+1)
When a transmission in state (m,0) is unsuccessful, the system will remain in the stage m but will pick a new random number uniformly from [0, Wm):
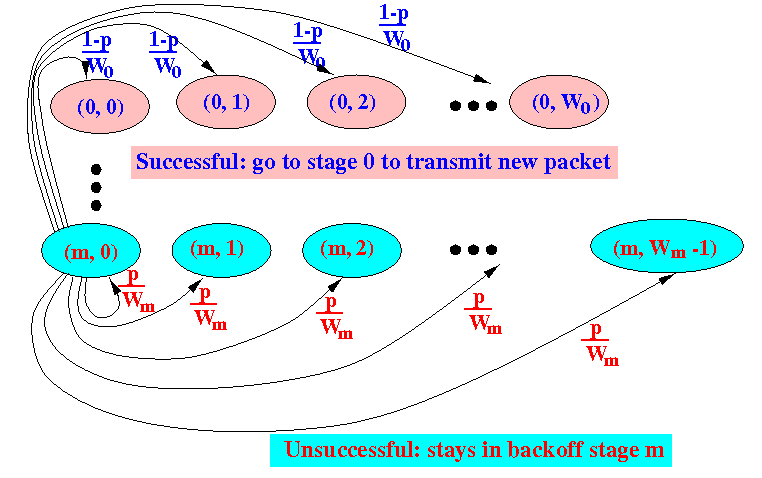
The probability that some number k ∈ [0, Wm) is picked is equal to 1/Wm
Therefore, the transition probability Ҏ{ m, k | m, 0 } from the state (m, 0) to the state (m, k) is:
1 Ҏ{ m, k | m, 0 } = ---- × p (for k = 0, 1, ..., Wm-1) ...... (3) Wm
- When a transmission in
state (i,0)
is successful, the system will
go to the stage 0
(this will happen at stage m also).
The station will immediately pick a new random number uniformly from [0, W0)
The probability that some number k ∈ [0, W0) is picked is equal to 1/W0
Therefore, the transition probability Ҏ{ 0, k | i, 0 } from the state (i, 0) (any i) to the state (0, k) is:
1 Ҏ{ i+1, k | i,0 } = ---- × (1 - p) (for k = 0, 1, ..., W0-1) ...... (4) W0
- From the state (i, j) where
j ≥ 1,
the next state is
always (i, j−1):
- When the station is in the state
(i, 0),
it will
transmit a packet immediately:

Therefore, the probability τ that a station transmits a packet is equal to:
-
τ =
b0,0 + b1,0 + ... + bm,0
(bi,j = the steady state probability that the system is in state (i,j))
-
τ =
b0,0 + b1,0 + ... + bm,0
- We will now
find the equilibrium equations
for the
steady state probabilities bi,j
- The order of treatment is:
- bi,0 for i = 1, 2, ..., m-1
- bm,0 (i.e., for
i = m)
- bi,k for i = 1, 2, ..., m-1 and k > 0
- bm,k for
k > 0
- b0,k for k > 0
|
|
- Focussing only on
how to reach the state (i,0)
for i = 1, 2, ..., m-1,
we see that:
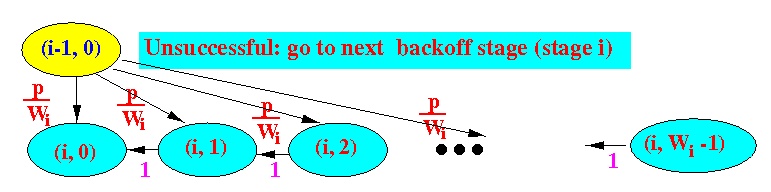
Therefore: (see: click here)
p p p bi,0 = --- × bi-1,0 + --- × 1 × bi-1,0 + ... + --- × 1 × .. × 1 × bi-1,0 Wi Wi Wi p <=> bi,0 = Wi --- × bi-1,0 Wi
bi,0 = p × bi-1,0 (for i = 1, 2, ..., m-1) ........ (E1)
- Equation (1) leads to the following
identifties:
b1,0 = p × b0,0 .... (E1a) b2,0 = p × b1,0 = p2 × b0,0 .... (E1b) b3,0 = p × b2,0 = p3 × b0,0 .... (E1c) ... bm-1,0 = pm-1 × b0,0 .... (E1x)
- The state (m,0) is a little
different because
we can reach (m, 0) in
2 different ways:
- from state (m-1,0) and
- from state (m,0)
See:

Therefore: (see: click here)
p p p bm,0 = --- × bm-1,0 + --- × 1 × bm-1,0 + ... + --- × 1 × .. × 1 × bm-1,0 Wm Wm Wm p p p + --- × bm,0 + --- × 1 × bm,0 + ... + --- × 1 × .. × 1 × bm,0 Wm Wm Wm p p <=> bm,0 = Wm --- × bm-1,0 + Wm --- × bm,0 Wm Wm <=> bm,0 = p × bm-1,0 + p × bm,0 <=> (1 - p ) bm,0 = p × bm-1,0
p bm,0 = ----- × bm-1,0 ........ (E2) 1-p
- Using Equations (1x) and (2),
we find that:
p bm,0 = ----- × bm-1,0 1-p p = ----- × pm-1 × b0,0 1-p pm = ----- × b0,0 ....... (E3) 1-p
- Focussing only on
how to reach the state (i,k)
for i = 1, 2, ..., m-1 and
k > 0,
we see that:
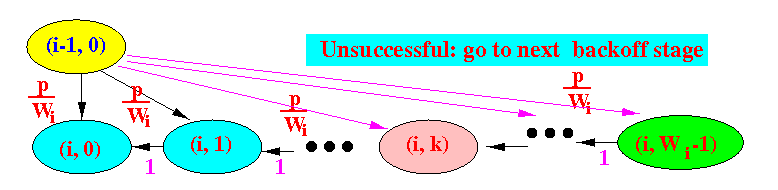
Therefore: (follow the magenta arrows in figure above) (see: click here)
p p p bi,k = --- × bi-1,0 + --- × 1 × bi-1,0 + ... + --- × 1 × .. × 1 × bi-1,0 (Wi-k terms) Wi Wi Wi p <=> bi,k = (Wi - k) × --- × bi-1,0 Wi
(Wi - k) bi,k = --------- × p × bi-1,0 (for i = 1, 2, ..., m-1 and k > 0) ........ (E4) Wi
- The state (m,k) is a little
different because
we can reach (m, k) in
2 different ways:
- from state (m-1,0) and
- from state (m,0)
See: (Follow the magenta arrows)
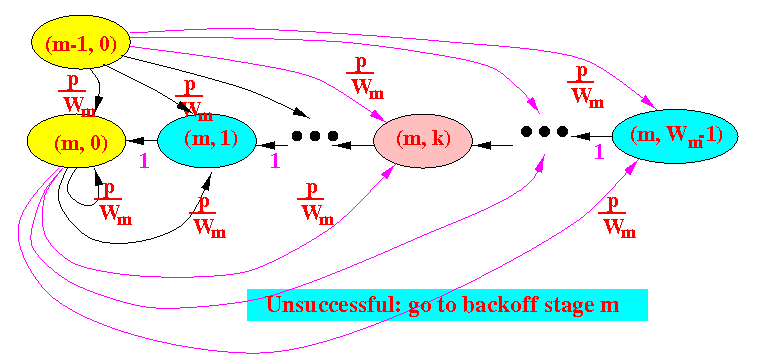
Therefore: (see: click here)
p p p bm,k = --- × bm-1,0 + --- × 1 × bm-1,0 + ... + --- × 1 × .. × 1 × bm-1,0 Wm Wm Wm p p p + --- × bm,0 + --- × 1 × bm,0 + ... + --- × 1 × .. × 1 × bm,0 Wm Wm Wm p p <=> bm,k = (Wm - k) --- × bm-1,0 + (Wm - k) --- × bm,0 Wm Wm
(Wm - k) bm,k = --------- × p × (bm-1,0 + bm,0) (for k > 0) ...... (E5) Wm
- The states (0, k) are
reached when a terminal
transmits a packet successfully
After a successful transmission, the terminal schedules the next packet by picking a random number from [0, W0)
- Focussing only on
how to reach the state (0,k)
for
k > 0,
we see that:

Therefore: (follow the magenta arrows in figure above) (see: click here)
1-p 1-p 1-p b0,k = ----- b0,0 + ----- × 1 × b0,0 + .... + ----- × 1 × ... × 1 × b0,0 W0 W0 W0 1-p 1-p 1-p + ----- b1,0 + ----- × 1 × b1,0 + .... + ----- × 1 × ... × 1 × b1,0 W0 W0 W0 + ..... 1-p 1-p 1-p + ----- bm,0 + ----- × 1 × bm,0 + .... + ----- × 1 × ... × 1 × bm,0 W0 W0 W0
1-p 1-p 1-p <=> b0,k = (W0 - k) ----- b0,0 + (W0 - k) ----- b1,0 + .... + (W0 - k) ----- bm,0 W0 W0 W0
W0 - k b0,k = -------- × (1-p) × (b0,0 + b1,0 + .... + bm,0) ...... (E6) W0
- Here are the equilibrium (steady state)
equations that we have found:
b1,0 = p × b0,0 .... (E1a) b2,0 = p2 × b0,0 .... (E1b) b3,0 = p3 × b0,0 .... (E1c) ... bm-1,0 = pm-1 × b0,0 .... (E1x) pm bm,0 = ----- × b0,0 ....... (E3) 1-p
(Wi - k) bi,k = --------- × p × bi-1,0 (for i = 1, 2, ..., m-1 and k > 0) ........ (E4) Wi (Wm - k) bm,k = --------- × p × (bm-1,0 + bm,0) (for k > 0) ...... (E5) Wm
W0 - k b0,k = -------- × (1-p) × (b0,0 + b1,0 + .... + bm,0) ...... (E6) W0We can simplify some of these equations....
- Using
Equations (E1a), (E1b), ..., (E1x)
and (E3),
we can express
bi,0 (for i = 1, 2, 3, ..., m)
in term of
b0,0 in the
Equations (E4), (E5) and (E6)
Results:
(Wi - k) bi,k = --------- × p × bi-1,0 (for i = 1, 2, ..., m-1 and k > 0) ........ (E4) Wi (Wi - k) = --------- × p × pi-1 × b0,0 Wi (Wi - k) = --------- × pi × b0,0 (for i = 1, 2, ..., m-1 and k > 0) ........ (E7) Wi
(Wi - k) bm,k = --------- × p × (bm-1,0 + bm,0) (for k > 0) ...... (E5) Wi (Wi - k) = --------- × p × (pm-1 × b0,0 + pm/(1-p) × b0,0) Wi (Wi - k) = --------- × pm × (b0,0 + p/(1-p) × b0,0) Wi (Wi - k) = --------- × pm × ((1-p)/(1-p) × b0,0 + p/(1-p) × b0,0) Wi (Wi - k) = --------- × pm × 1/(1-p) × b0,0 ...... (E8) Wi
W0 - k b0,k = -------- × (1-p) × (b0,0 + b1,0 + .... + bm,0) ...... (E6) W0 W0 - k = -------- × (1-p) × (b0,0 + p × b0,0 + p2 × b0,0 + .... + pm-1 × b0,0 + pm/(1-p) × b0,0) W0 W0 - k = -------- × (1-p) × (1 + p + p2 + .... + pm-1 + pm/(1-p)) × b0,0 W0S = 1 + p + p2 + .... + pm-1 p×S = p + p2 + .... + pm-1 + pm Subtract these 2 equations: => (1-p)×S = 1 - pm 1 - pm <=> S = ------- 1 - p
- Summary:
b1,0 = p × b0,0 .... (E1a) b2,0 = p2 × b0,0 .... (E1b) b3,0 = p3 × b0,0 .... (E1c) ... bm-1,0 = pm-1 × b0,0 .... (E1x) pm bm,0 = ----- × b0,0 ....... (E3) 1-p
(Wi - k) bi,k = --------- × pi × b0,0 (for i = 1, 2, ..., m-1 and k > 0) ........ (E7) Wi (Wi - k) bm,k = --------- × pm × 1/(1-p) × b0,0 ...... (E8) Wi
W0 - k b0,k = -------- × b0,0 ....... (E9) W0
- The value of b0,0 can
be found by using the fact that
the sum of
all state probabilities is
equal to 1 (one):
b0,0 + b0,1 + .... + b0,W0 + b1,0 + b1,1 + .... + b1,W1 + .... + bm,0 + bm,1 + .... + bm,Wm = 1
- I did not work it out and will
quote the result in the paper:
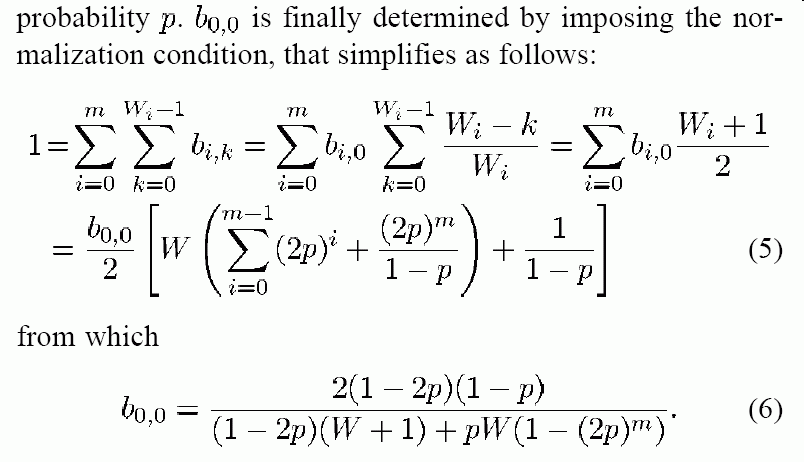
Note:
- W = CWmin
(see: click here )
This value is set by the 802.11 protocol
- p = probability that a transmission
will be in a collision
This value depends on τ (how likely a station will transmit) and it has not yet been undetermined
- W = CWmin
(see: click here )
- Recall that
τ is equal to
(see: click here)
-
τ =
b0,0 + b1,0 + ... + bm,0
(bi,j = the steady state probability that the system is in state (i,j))
-
τ =
b0,0 + b1,0 + ... + bm,0
- Using:
b1,0 = p × b0,0 .... (E1a) b2,0 = p2 × b0,0 .... (E1b) b3,0 = p3 × b0,0 .... (E1c) ... bm-1,0 = pm-1 × b0,0 .... (E1x) pm bm,0 = ----- × b0,0 ....... (E3) 1-pand the expression for b0,0, we find:
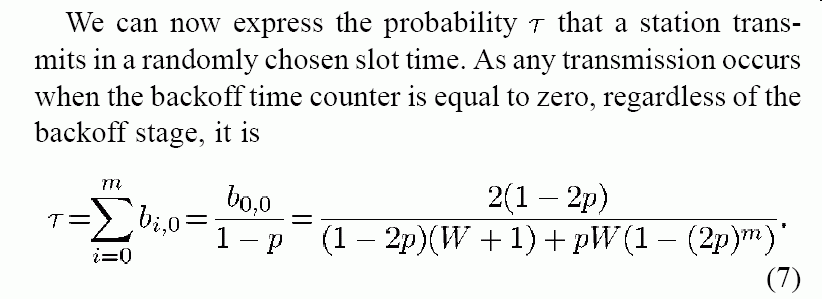
Note:
- W = CWmin
(see: click here )
This value is set by the 802.11 protocol
- p = probability that a transmission
result in a collision
This value depends on τ (how likely a station will transmit) and it has not yet been undetermined
- W = CWmin
(see: click here )
- We now find the value of
p (probability that a
transmission results in a collision
- When a station transmits, the packet transmission
will be successful if
all other n−1 stations
does not transmit
The probability of this event is:
- Ҏ[ successul transmission] = (1 − τ)n−1
- Therefore:
- p = Ҏ[ unsuccessul transmission] = 1 − (1 − τ)n−1 ...... (9)
- The Equations (7) and (9)
in the paper
form a
non-linear system to
compute the values of
τ and
p:
2(1-2p) τ = ---------------------------- ...... (7) (1-2p)(W+1) + pW(1 - (2p)m) p = 1 - (1-τ)n-1 ...... (9) - You can use any
numerical approximation techniques
(such as the
iterative approximation method)
to find a solution
I will use Maple...
- Example: n = 10, W = 16, m = 10
2(1-2p) 2(1-2p) τ = ------------------------------ = --------------------------- (1-2p)(16+1) + 16p(1 - (2p)10) 17(1-2p) + 16(1 - (2p)10) p = 1 - (1-τ)10-1 = 1 - (1-τ)9Using Maple:
> eq1 := tau = 2*(1-2*p)/(17*(1-2*p) + 16*(1 - (2*p)^10)); 2 (1 - 2 p) eq1 := tau = --------------------- 10 33 - 34 p - 16384 p > eq2 := p = 1 - (1 - tau)^9; 9 eq2 := p = 1 - (1 - tau) > fsolve( {eq1, eq2}, {tau, p} ); {p = 0.2865008129, tau = 0.03681349985}