Slideshow:
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Problem description:
Find the best algorithm to execute ⋈1 and ⋈2 for M = 101 - click to pull out
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Simplified Problem :
Solution method: brute force search for the min. cost algorithms that can operate with M = 101
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 1: check if we can use a 1-pass algorithm for ⋈1:
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 2: check if we can use a 2-pass (hashing based) algorithm for ⋈1:
Next, we find the best algorithm for ⋈2 (considering the buffer utilization of ⋈1 !)
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Determining the buffer utilization by the ⋈1 execution:
(⋈2 is inactive and will not use any buffers)
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Determining the buffer utilization by the ⋈1 execution:
Next: we run pass 2 of the 2-pass (hashing-based) algorithm (= a 1-pass algorithm on each Ri and Si)
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Determining the buffer utilization by the ⋈1 execution:
Note: pass 2 is run for every chunk Ri and Si and pass 2 will output tuples to ⋈2 (→ becomes active !)
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Cost (so far):
Click on image to pull out (keep running cost)
Next: determine the best suitable join algorithm for ⋈2
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Prelude to considering the implementation algorithm for ⋈2:
⋈1 is actively using its buffers to produce tuples for ⋈2:
I.e.: we must find the best algorithm for ⋈2 using M = 101 − 51 = 50 buffers !!
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 3: check if we can use a 1-pass algorithm for ⋈2:
Therefore: we cannot use the 1-pass join algorithm
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 4: check if we can use a 2-pass (hashing based) algorithm for ⋈2:
Note: B(R⋈1S) > 5000. Therfore: B(R⋈1S)/50 > 100 (each chunk of the first relation of ⋈2 > 100 blks)
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 4: check if we can use a 2-pass (hashing based) algorithm for ⋈2:
Therefore: we cannot use 2-pass algorithm to execute ⋈2
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 5: check if we can use a 3-pass (hashing based) algorithm for ⋈2:
Note: each "sub-sub-relation chunk is about B(R⋈S)/(502) blks
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 5: check if we can use a 3-pass (hashing based) algorithm for ⋈2:
Next, we hash the 2nd input relation T in the same manner...
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 5: check if we can use a 3-pass (hashing based) algorithm for ⋈2:
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 5: check if we can use a 3-pass (hashing based) algorithm for ⋈2:
Notice that:
size of each sub-sub-relation of
R⋈1S is
> 5000/2500 = 2 blks
size of each sub-sub-relation of
T is
= 10000/2500 = 4 blks
So pass 3 may use Tij (chunks of T) as build relation if R⋈1S > 10000 !
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Step 5: check if we can use a 3-pass (hashing based) algorithm for ⋈2:
Therefore: we can always use the 3-pass algorithm for bowtie;2 when B(R⋈1S) > 5000
Example on selection implementation algorithm for a query plan -
B(R⋈S) large
Cost analysis:
- Consider the following
modified scenario
for
the same
query plan:
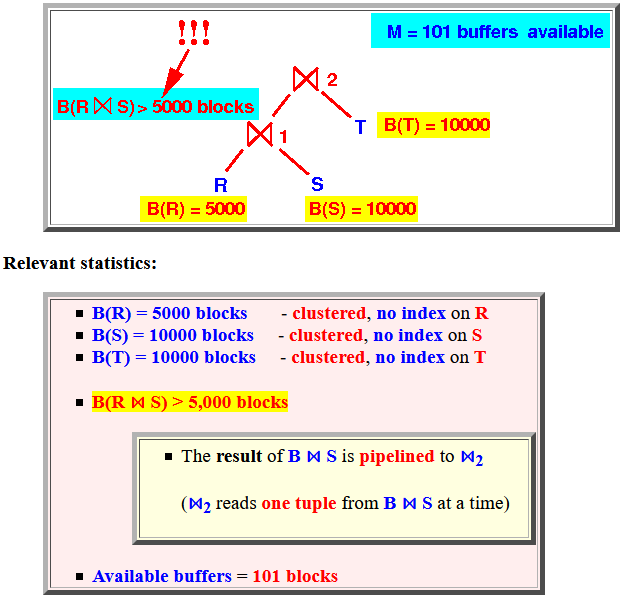
Relevant statistics:
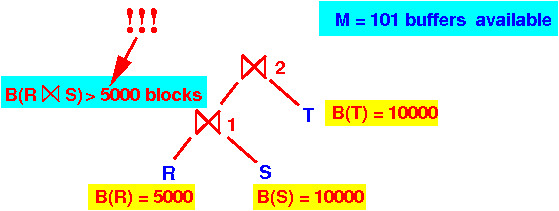
- B(R) = 5000 blocks - clustered, no index on R
- B(S) = 10000 blocks - clustered, no index on S
- B(T) = 10000 blocks
-
clustered,
no index
on T
-
B(R ⋈ S)
> 5,000 blocks
- The result of
B ⋈ S is
pipelined to
⋈2
(⋈2 reads one tuple from B ⋈ S at a time)
- The result of
B ⋈ S is
pipelined to
⋈2
- Available buffers = 101 blocks
- Choice
for the join algorithm:
- One-pass join algorithm (see: click here)
- 2-pass join algorithm based on hashing (see: click here)
- 3-pass join algorithm based on hashing (see: click here)
- Problem:
- Determine
the minimum cost algorithm
you can use for
⋈1 and
⋈2
- Determine the total # disk IOs incurred by the physical query plan
- Determine
the minimum cost algorithm
you can use for
⋈1 and
⋈2
- Step 1:
check if
we can use a 1-pass algorithm
for ⋈1:
-
We have performed this
check
before:
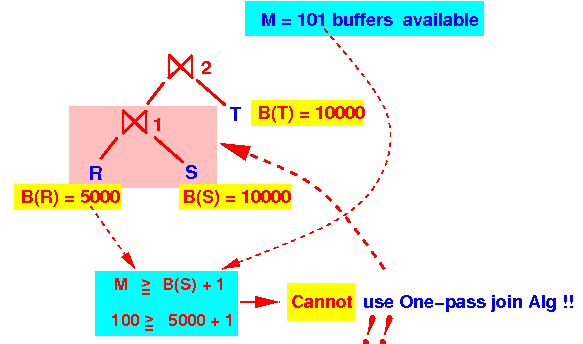
Since:
M = 101 < 5001We cannot use a 1-pass algorithm for ⋈1
-
We have performed this
check
before:
- Step 2:
check if we can use
a
2-pass (hashing based)
join algorithm for
⋈2
-
We have performed this
check
before:
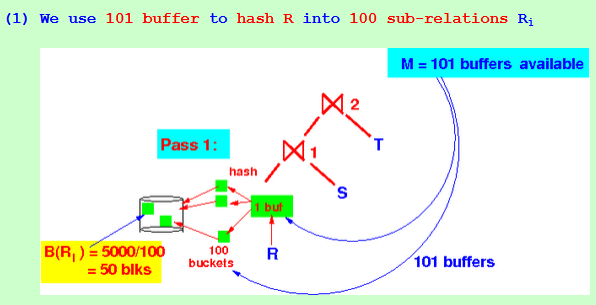
How is the ⋈1 executed:
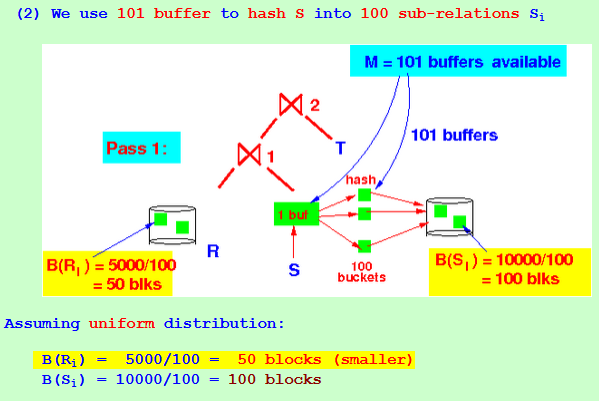
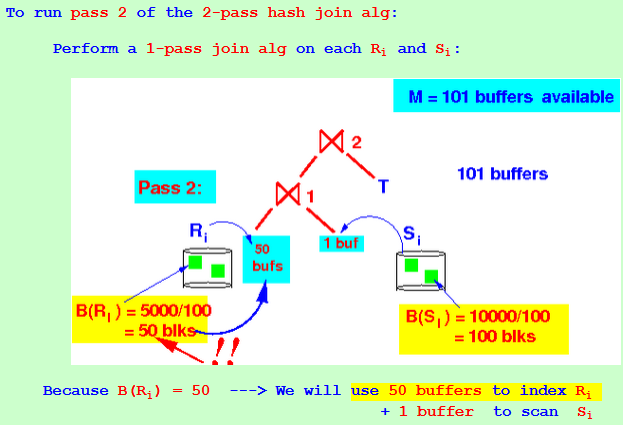
Pass 1 of the 2-pass hash join alg: (1) We use 101 buffer to hash R into 100 sub-relations Ri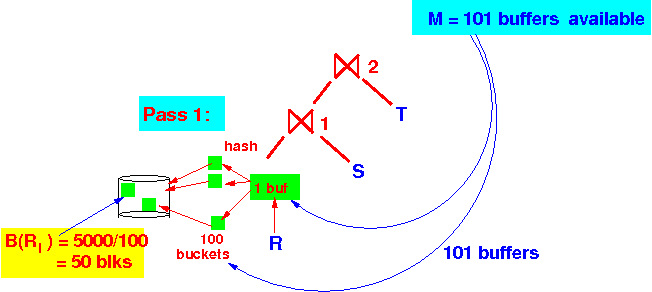
(2) Use 101 buffer to hash S into 100 sub-relations Si
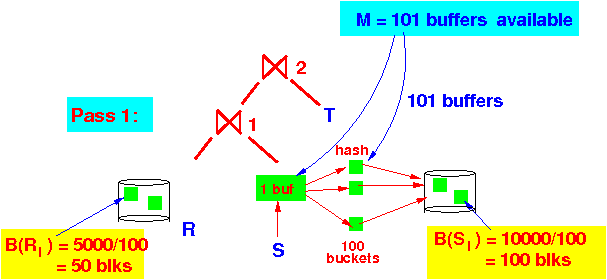Assuming uniform distribution:
B(Ri) = 5000/100 = 50 blocks (smaller)
B(Si) = 10000/100 = 100 blocks
Pass 2 of the 2-pass hash join alg: Perform a 1-pass join alg on each Ri and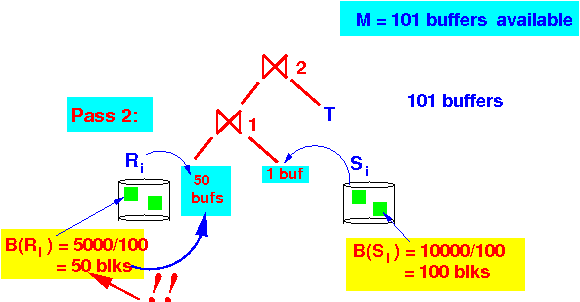 Si:
Because B(Ri) = 50 ---> We will only use 50 buffers to index Ri
+ 1 buffer to scan Si
-
We have performed this
check
before:
-
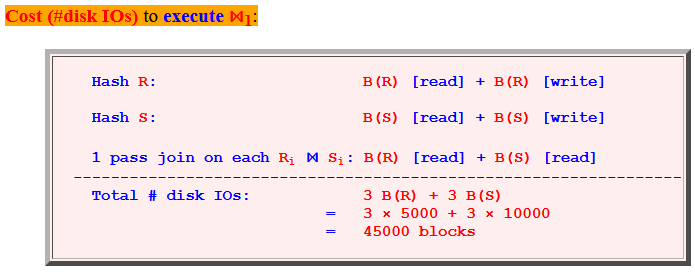
Determine the cost (#disk IOs)
to execute
⋈1:
SAME !!!
Hash R: B(R) [read] + B(R) [write] Hash S: B(S) [read] + B(S) [write] 1 pass join on each Ri ⋈ Si: B(R) [read] + B(S) [read] ----------------------------------------------------------------- Total # disk IOs: 3 B(R) + 3 B(S) = 3 × 5000 + 3 × 10000 = 45000 blocks
-
Step 3:
determine the best suitable
join algorithm for
⋈2:
- We will get a different outcome because B(R ⋈S) > 5000
- From
the previous discussion,
we know that the
following algorithms
are
unsuitable:
- ⋈2
can not use a
1-pass
join algorithm based on
hashing
because:
-
1-pass algorithm for
⋈2 requires
B(R⋈S) buffers
(≥ 5000)
- Given: B(R⋈S) (≥ 5000) > 50 (= available buffers)
Graphically:
-
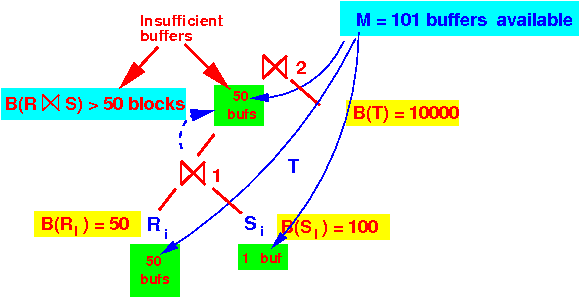
1-pass algorithm for
⋈2 requires
B(R⋈S) buffers
(≥ 5000)
- ⋈2
can not use a
2-pass
join algorithm based on
hashing
can not be
used because:
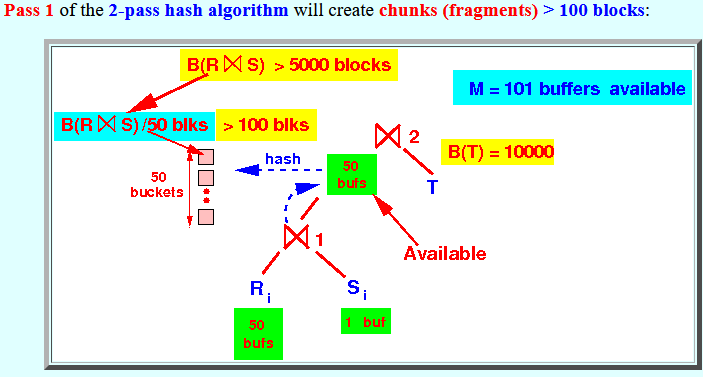
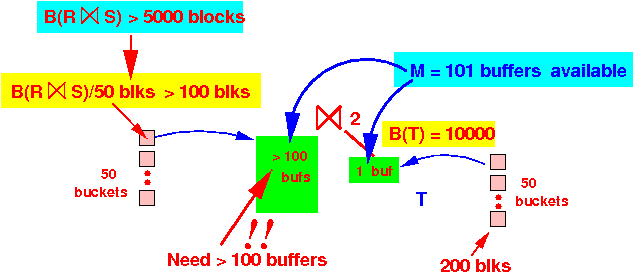
- The chunks used in
pass 2 of the
2-pass hashing
⋈2 are
> 100 blocks
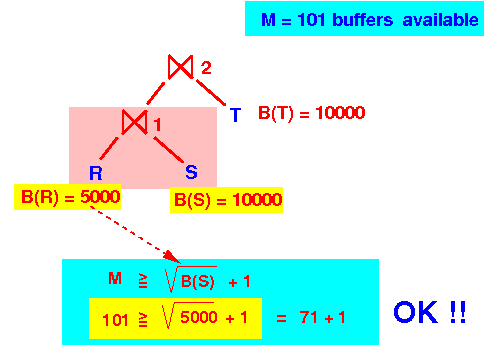
- We only have (M−1) = 100 buffers available to index (search structure) each chuck in pass 2
Graphically:
- Pass 1 of the
2-pass hash algorithm
will create
chunks (fragments)
> 100 blocks:
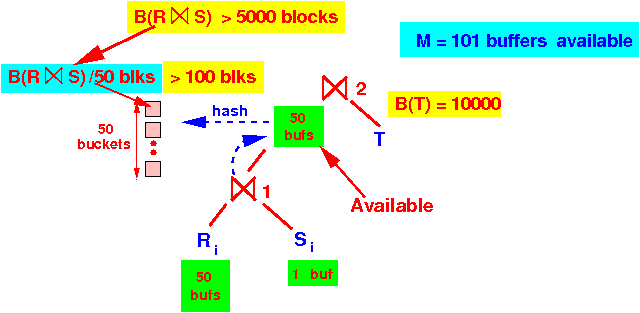
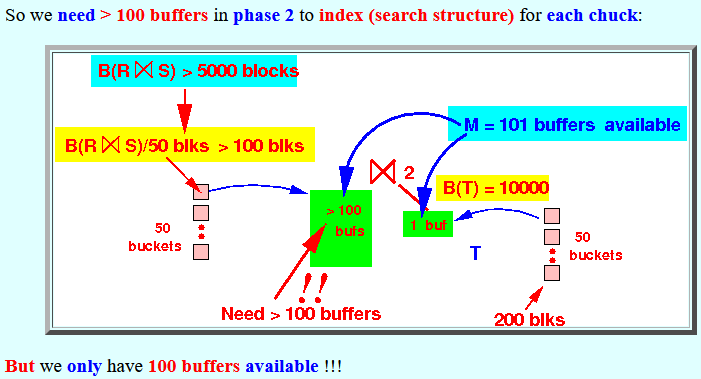
- So we need
> 100 buffers
in phase 2
to index (search structure)
for each chuck:
But we only have 100 buffers available !!!
- The chunks used in
pass 2 of the
2-pass hashing
⋈2 are
> 100 blocks
- ⋈2
can not use a
1-pass
join algorithm based on
hashing
because:
- Check if we can
use the 3-pass
join algorithm for
⋈2:
- We will use the
remaining
50 (= 101 - (50 + 1)) buffers/buckets
to
hash
of R ⋈ S
two times onto
disk:
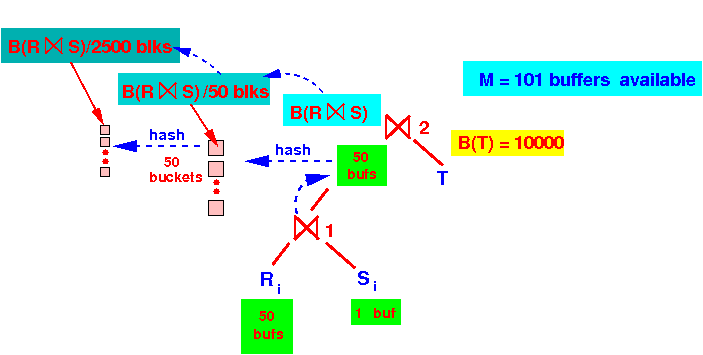
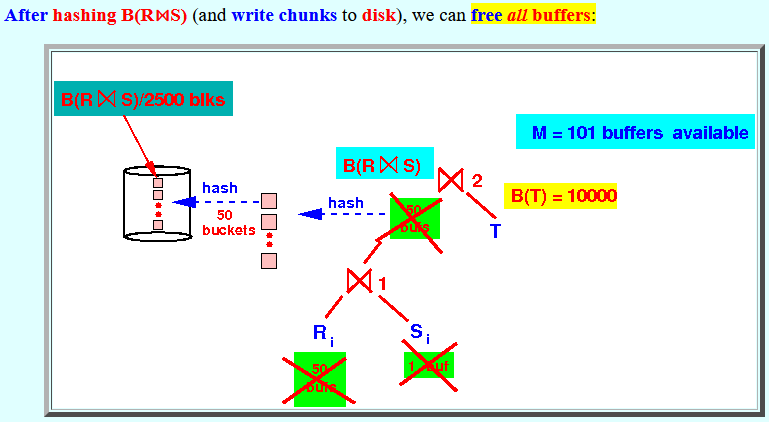
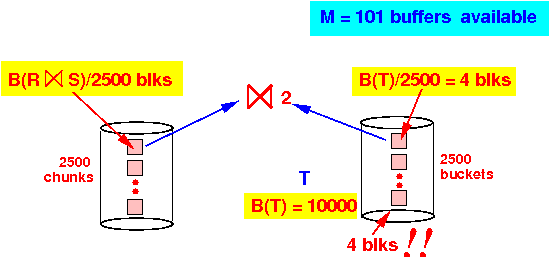
Each "sub-sub-relation" chunk Rij has the size B(R⋈S)/2500
- As we will see soon, the chunk size of Rij will be irrelevant...
After hashing B(R⋈S) (and write chunks to disk), we can free all buffers:
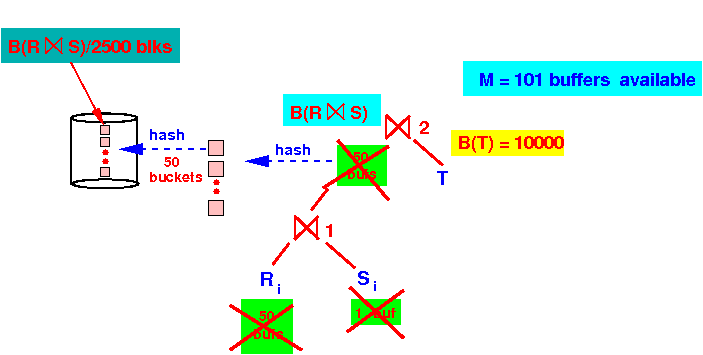
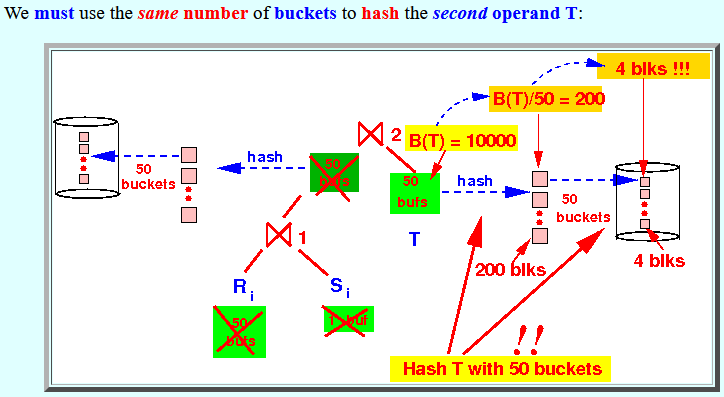
- We must use the
same number of
buckets to
hash the
second operand T:
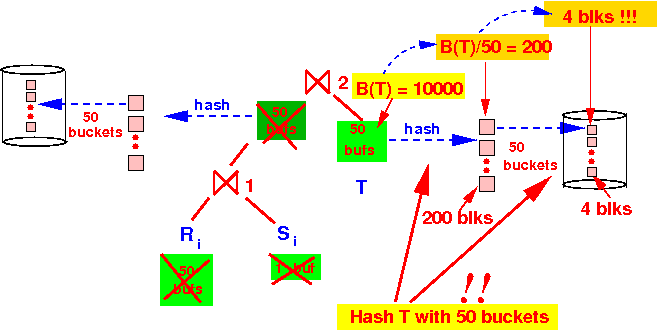
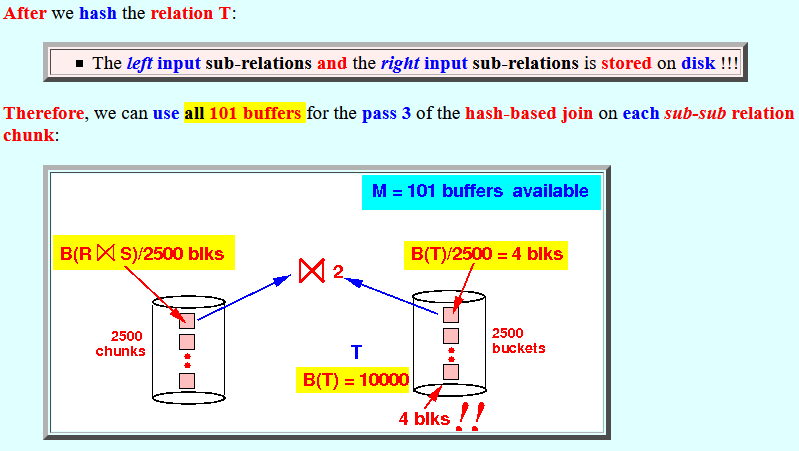
- After
we hash
the relation T:
- The left input sub-relations and the right input sub-relations is stored on disk !!!
Therefore, we can use all 101 buffers for the pass 3 of the hash-based join on each sub-sub relation chunk:
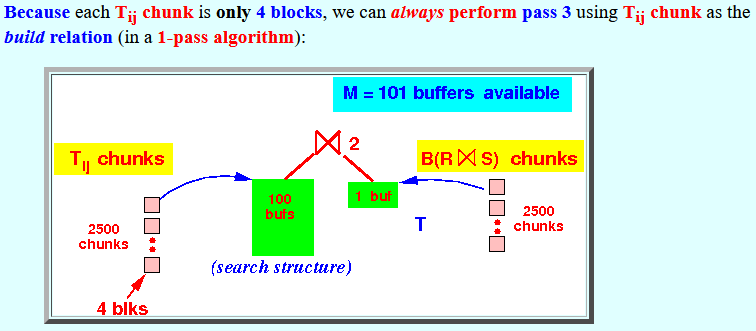
Because each Tij chunk is only 4 blocks, we can always perform pass 3 using Tij chunk as the build relation (in a 1-pass algorithm):
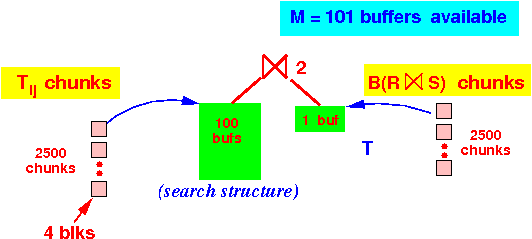
Pass 3 of the 3-pass hash-based join is the one-pass join algorithm:
- Each chunk of Tij is B(T)/2500 = 10000/2500 = 4 blocks
- We can use 100 buffers to build the search structure
Conclusion:
- If B(R⋈S) > 5,000, then we can use (always) a 3-pass hash-based join algorithm for ⋈2
- We will use the
remaining
50 (= 101 - (50 + 1)) buffers/buckets
to
hash
of R ⋈ S
two times onto
disk:
-
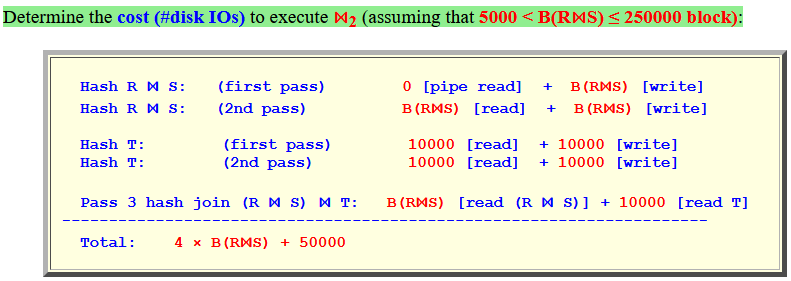
Determine the cost (#disk IOs)
to execute
⋈2
(assuming that
5000 < B(R⋈S) ≤ 250000 block):
Hash R ⋈ S: (first pass) 0 [pipe read] + B(R⋈S) [write] Hash R ⋈ S: (2nd pass) B(R⋈S) [read] + B(R⋈S) [write] Hash T: (first pass) 10000 [read] + 10000 [write] Hash T: (2nd pass) 10000 [read] + 10000 [write] Pass 3 hash join (R ⋈ S) ⋈ T: B(R⋈S) [read (R ⋈ S)] + 10000 [read T] --------------------------------------------------------------------- Total: 4 × B(R⋈S) + 50000
# disk IOs for ⋈1 = 45000 # disk IOs for ⋈2 = 4×B(R⋈S) + 50000 ------------------------------------------------------- Total # disk IOs = 4×B(R⋈S) + 95000 |