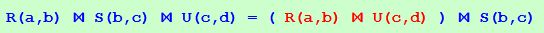---

Estimating the size of the result of R ⋈ S when joining on multiple attributes

---

---

---

 

Slideshow:

Estimating the size of the result of R⋈S when joining on multiple attributes - problem description
 
Note: the independence assumption allows us to use the multiplication rule in Probabilities
Probability that r ∈ R and s ∈ S will join (and produce a tuple)
When will r ⋈ s produce a tuple in result:

Individual probabilities of each type of event (from last webpage):

Probability that r ∈ R and s ∈ S will join (and produce a tuple)
When will r ⋈ s produce a tuple in result:

Individual probabilities of each type of event (from last webpage):

Assuming that the attribute values of Y1 and Y2 are independent, we have: (multiply rule)

Estimating the join result set R(X,Y₁,Y₂) ⋈ S(Y₁,Y₂,Z)
 
An arbitrary tuple s ∈ S and an arbitrary tuple r ∈ R will produce a join tuple with probability 1/(max(V(R,Y1)...):

Estimating the join result set R(X,Y₁,Y₂) ⋈ S(Y₁,Y₂,Z)
 
Then: an arbitrary tuple s ∈ S joining with all tuple r ∈ R will produce:   1/max(V(R,Y1).. × T(R) tuples

Estimating the join result set R(X,Y₁,Y₂) ⋈ S(Y₁,Y₂,Z)
 
Finally: joining all tuples s ∈ S with all tuple r ∈ R will produce:   T(S) × 1/max(V(R,Y1)... × T(R) tuples

Estimation formula:  
T( R(X,Y₁,Y₂) ⋈ S(Y₁,Y₂,Z) ) = T(R) × T(S) / ( max( V(R,Y₁), V(S,Y₁) ) × max( V(R,Y₂), V(S,Y₂) )
Estimating the join result set R(X,Y₁,Y₂) ⋈ S(Y₁,Y₂,Z) - Example 3
 
Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 3

Method 3:

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 3

Method 3:

Note:

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 3

Method 3:

Estimate for the # tuples in R(a,b) ⋈ U(c,d):

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 3

Method 3:

Estimate for the # tuples in R(a,b) ⋈ U(c,d) = 5,000,000
Estimate for the # tuples in R(a,b) ⋈ U(c,d) ⋈ S(b,c):

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 3

Method 3:

Estimate for the # tuples in R(a,b) ⋈ U(c,d) = 5,000,000
Estimate for the # tuples in R(a,b) ⋈ U(c,d) ⋈ S(b,c):


Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 3

Method 3:

Estimate for the # tuples in R(a,b) ⋈ U(c,d) = 5,000,000
Estimate for the # tuples in R(a,b) ⋈ U(c,d) ⋈ S(b,c):

Comment and observation
We got the same answer as before:


❮ ❯



---

---

---

---

• Estimating T(R⋈S) when joining on 2 attributes
  • Given:

    W = R(X,Y1,Y2) ⋈ S(Y1,Y2,Z)

    What is an estimate for size of   R(X,Y₁,Y₂) ⋈ S(Y₁,Y₂,Z) ???

    ---

    ---

  • Assumption:

    The attribute values in Y1 and Y2 are independent

    ---

    ---

  • Fact:

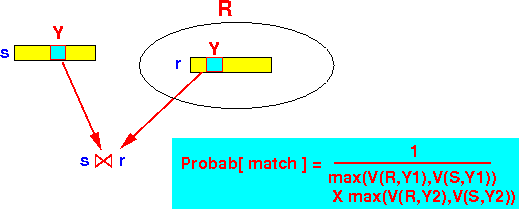
    The tuples r ∈ R and s ∈ S will join and produce a tuple in the result is when: r(Y1) = s(Y1) and r(Y2) = s(Y2)

    Previously, we have found that:

    1 Probab[ r(Y1) = s(Y1) ] = ------------------------- max( V(R,Y1), V(S,Y1) ) 1 Probab[ r(Y2) = s(Y2) ] = ------------------------- max( V(R,Y2), V(S,Y2) )

    ---

    ---

  • Assuming that the attribute values of Y1 and Y2 are independent, we have:

    Probab[ r(Y1) = s(Y1) and r(Y2) = s(Y2) ] 1 = --------------------------------------------------- max( V(R,Y1), V(S,Y1) ) × max( V(R,Y2), V(S,Y2) )

    ---

    ---

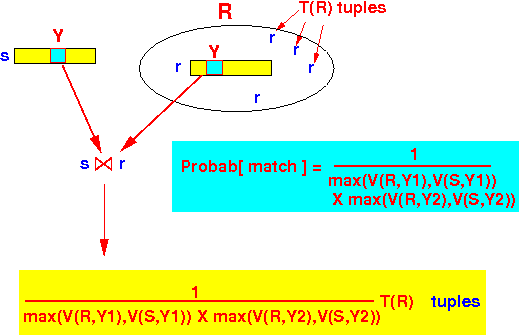
  • Using the same reasoning, we find that:

    T( R(X,Y1,Y2) ⋈ S(Y1,Y2,Z) ) T(R) × T(S) = --------------------------------------------------- max( V(R,Y1), V(S,Y1) ) × max( V(R,Y2), V(S,Y2) )

  ---

  ---

  ---

  ---

• Example: estimating the size of a join operation
  • Information on the input relations:

    R(a,b) S(b,c) U(c,d) ======================================================= T(R) = 1000 T(S) = 2000 T(U) = 5000 V(R,b) = 20 V(S,b) = 50 V(S,c) = 100 V(U,c) = 500

    Problem:

    Estimate the size of R ⋈ S ⋈ U

    computed using this ordering:

    R(a,b) ⋈ S(b,c) ⋈ U(c,d) = ( R(a,b) ⋈ U(c,d) ) ⋈ S(b,c)

    ---

    ---

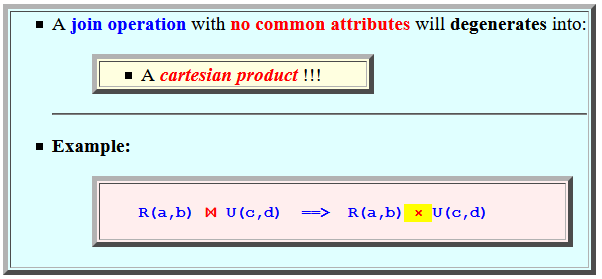
  • Pre-requisite: a join with no common attributes

    A join operation with no common attributes will degenerates into: A cartesian product !!!          Example: R(a,b) ⋈ U(c,d) ==> R(a,b) × U(c,d)

    ---

    ---

  • Method 3: (ordering 3)

    R(a,b) ⋈ S(b,c) ⋈ U(c,d) = ( R(a,b) ⋈ U(c,d) ) ⋈ S(b,c) T( R(a,b) ⋈ U(c,d) ) = T (R(a,b) × U(c,d) ) // Cartesian product !! = 1000 × 5000 = 5,000,000 ............................ (1) The estimate of the size the join ( R(a,b) ⋈ U(c,d) ) ⋈ S(b,c) is: T( R(a,b) ⋈ U(c,d) ) × T(S) ~= ------------------------------------------------------------- max( V(R(a,b) ⋈ U(c,d),b), V(S,b) ) × max( V(**,c), V(S,c) ) ^^^^^^^^^^^^^^^^^^^^ ** = R(a,b) ⋈ U(c,d) From the preservation of value sets assumption, we have: V(R(a,b) ⋈ U(c,d),b) = V(R,b) // V(R,b) = 20 according to data = 20 ...................... (2) V(R(a,b) ⋈ U(c,d),c) = V(U,c) // V(U,c) = 500 according to data = 500 ...................... (3) Therefore: T( R(a,b) ⋈ U(c,d) ) × T(S) T( R ⋈ S ⋈ U ) ~= ------------------------------------------------------- max( V(R(a,b) ⋈ U(c,d),b), V(S,b) ) × max( V(**,c), V(S,c) ) 5,000,000 × 2,000 ~= --------------------------------- max( 20, 50 ) × max( 500, 100 ) 5,000,000 × 2,000 ~= ------------------- 50 × 500 100,000 × 2,000 ~= ------------------- 500 ~= 100,000 × 4 ~= 400,000 ----- answer

    Notice that:

    We got the same answer as before: click here The 2 assumptions (containment and preservation of value sets) allows you to re-order the join-order without affecting the size of the result set estimation (The text book mentioned that this phenomenon can be proved formally but provides no proof.....)