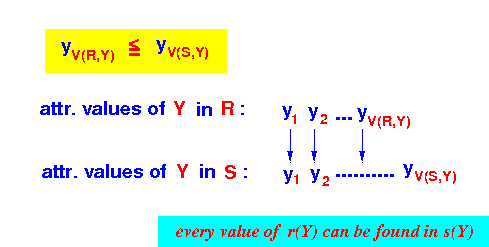---

Estimating the size of the result of R⋈S when joining on 1 attribute

---

---

---

 

Slideshow:

Estimating the size of the result of R⋈S when joining on 1 attribute - problem description
 
Estimating the size of the result of R⋈S when joining on 1 attribute - problem description
   
Estimating the size of the result of R⋈S when joining on 1 attribute - problem description
   
We randomly select a tuple r ∈ relation R and a tuple s ∈ relation S.

I.e.: what's the probability that r and s will produce a tuple ?
Probability that r ∈ R and s ∈ S will join (and produce a tuple)
 
The computation is handled differently in 2 different cases:
V(S, Y) ≤ V(R, Y)   (i.e.: attribute Y in R takes on more different values) V(R, Y) ≤ V(S, Y)   (i.e.: attribute Y in S takes on more different values)
Probability that r ∈ R and s ∈ S will join (and produce a tuple) - V(S, Y) ≤ V(R, Y)

Probability that r ∈ R and s ∈ S will join (and produce a tuple) - V(S, Y) ≤ V(R, Y)
 
Estimating the join result set R(X,Y) ⋈ S(Y,Z) - V(S, Y) ≤ V(R, Y)
 
An arbitrary tuple s ∈ S and an arbitrary tuple r ∈ R will produce a join tuple with probability 1/V(R,Y):

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - V(S, Y) ≤ V(R, Y)
 
Then: an arbitrary tuple s ∈ S joining with all tuple r ∈ R will produce:   1/V(R,Y) × T(R) tuples

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - V(S, Y) ≤ V(R, Y)
 
Finally: joining all tuples s ∈ S with all tuple r ∈ R will produce:   T(S) × 1/V(R,Y) × T(R) tuples

Estimation formula:   T( R(X,Y) ⋈ S(Y,Z) ) = T(R) × T(S) / V(R,Y)
Probability that r ∈ R and s ∈ S will join (and produce a tuple) - V(R, Y) ≤ V(S, Y)

Probability that r ∈ R and s ∈ S will join (and produce a tuple) - V(R, Y) ≤ V(S, Y)
 
Estimating the join result set R(X,Y) ⋈ S(Y,Z) - V(R, Y) ≤ V(S, Y)
 
An arbitrary tuple r ∈ R and an arbitrary tuple s ∈ S will produce a join tuple with probability 1/V(S,Y):

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - V(R, Y) ≤ V(S, Y)
 
Then: an arbitrary tuple r ∈ R joining with all tuple s ∈ S will produce:   1/V(S,Y) × T(S) tuples

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - V(R, Y) ≤ V(S, Y)
 
Finally: joining all tuples r ∈ R with all tuple s ∈ S will produce:   T(R) × 1/V(S,Y) × T(S) tuples

Estimation formula:   T( R(X,Y) ⋈ S(Y,Z) ) = T(R) × T(S) / V(S,Y)
Estimating the join result set R(X,Y) ⋈ S(Y,Z) - combined result
Summary of the finding:
V(S, Y) ≤ V(R, Y)   (i.e.: attribute Y in R takes on more different values) T(R) × T(S) T( R ⋈ S ) = ----------- V(R,Y) V(R, Y) ≤ V(S, Y)   (i.e.: attribute Y in S takes on more different values) T(R) × T(S) T( R ⋈ S ) = ----------- V(S,Y)

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 1
 
Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 1

Method 1:

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 1

Method 1:

Estimate for the # tuples in R(a,b) ⋈ S(b,c):

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 1

Method 1:

Estimate for the # tuples in R(a,b) ⋈ S(b,c) = 40,000
Estimate for the # tuples in ( R(a,b) ⋈ S(b,c) ) ⋈ U(c,d): (same formula)

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 1

Method 1:

Estimate for the # tuples in R(a,b) ⋈ S(b,c) = 40,000
Estimate for the # tuples in ( R(a,b) ⋈ S(b,c) ) ⋈ U(c,d): (same formula)
 
Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 1

Method 1:

Estimate for the # tuples in R(a,b) ⋈ S(b,c) = 40,000
Estimate for the # tuples in ( R(a,b) ⋈ S(b,c) ) ⋈ U(c,d): (same formula)

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 2 (same join, different order)
 
Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 2

Method 2:

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 2

Method 2:

Estimate for the # tuples in S(b,c) ⋈ U(c,d):

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 2

Method 2:

Estimate for the # tuples in S(b,c) ⋈ U(c,d) = 20,000
Estimate for the # tuples in R(a,b) ⋈ ( S(b,c) ⋈ U(c,d) ) : (same formula)

Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 2

Method 2:

Estimate for the # tuples in S(b,c) ⋈ U(c,d) = 20,000
Estimate for the # tuples in R(a,b) ⋈ ( S(b,c) ⋈ U(c,d) ) : (same formula)
 
Estimating the join result set R(X,Y) ⋈ S(Y,Z) - Example 2

Method 2:

Estimate for the # tuples in S(b,c) ⋈ U(c,d) = 20,000
Estimate for the # tuples in R(a,b) ⋈ ( S(b,c) ⋈ U(c,d) ) : (same formula)

Postscript...
 
❮ ❯



---

---

---

---

• Estimating T(R⋈S) when joining on one attribute
  • Given:

    W = R(X,Y) ⋈ S(Y,Z)           Y is one attribute in both relations

    What is an estimate for size of T( R(X,Y) ⋈ S(Y,Z) ) ???

    ---

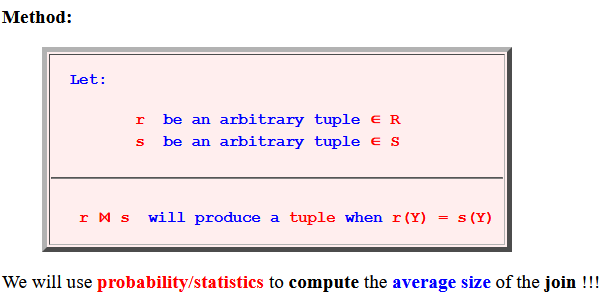
  • Method:

    Let: r be an arbitrary tuple ∈ R s be an arbitrary tuple ∈ S r ⋈ s will produce a tuple when r(Y) = s(Y)

    We will use probability/statistics to compute the average size of the join !!!

    ---

    ---

  • 64,000 question:

    What is the probability (chance) that r(Y) = s(Y) ???

    ---

    ---

  • Case 1: V(R,Y) ≥ V(S,Y)

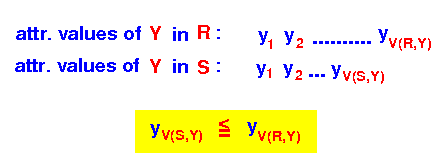
    The tuples in relations R and S take on the following attribute values for the Y attribute: Therefore, by the containment of value sets assumption, we have that: ∀ tuple s ∈ S: s(Y) ∈ set of values of Y in R Graphically: We can compute the probability that 2 tuples (one from R and one from S) join as follows: Let: r be an arbitrary tuple ∈ R s be an arbitrary tuple ∈ S Probab[ r and s join ] = Probab[ r(Y) = s(Y) ] // They have same value in Y attr To compute this probability, consider one fixed value s(Y): 1 Probab[ r(Y) = s(Y) ] = ------ (one "good" out of V(R,Y) possible !!!) V(R,Y) Using this probability, the number of tuples in R(X,Y) ⋈ S(Y,Z) can be estimated as follows: The probability of a match between a tuple in S and R is: 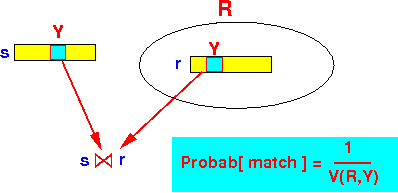There are T(R) tuples in R. 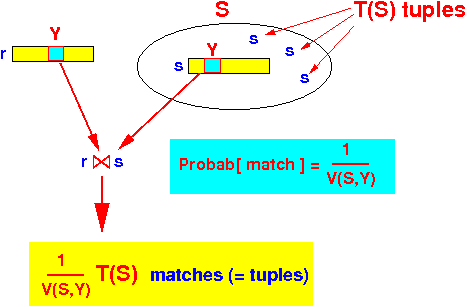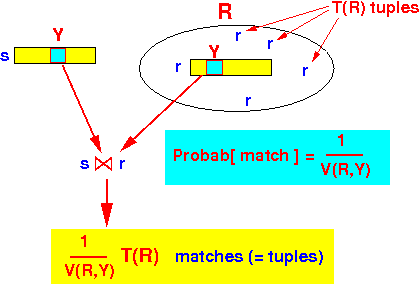Therefore, one tuple s ∈ S will produce this many # of matches: There are T(S) tuples in S. Each tuple s ∈ S produces T(R)/V(R,Y) number of matches (= tuples). Therefore: T(R) × T(S) T( R ⋈ S ) = ----------- V(R,Y)

    ---

    ---

    ---

  • Case 2: V(S,Y) ≥ V(R,Y) (same reasoning, replace the roles of R and S)

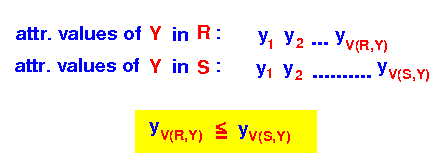
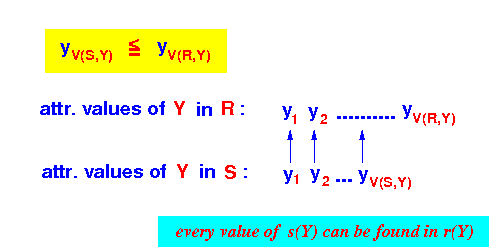
    The tuples in relations R and S take on the following attribute values for the Y attribute: Therefore, by the containment of value sets assumption, we have that: ∀ tuple r ∈ R: r(Y) ∈ set of values of Y in S We can compute the probability that 2 tuples (one from R and one from S) join as follows: Let: r be an arbitrary tuple ∈ R s be an arbitrary tuple ∈ S Probab[ r and s join ] = Probab[ r(Y) = s(Y) ] // They have same value in Y attr To compute this probability, consider one fixed value r(Y): 1 Probab[ r(Y) = s(Y) ] = ------ (one "good" out of V(S,Y) possible !!!) V(S,Y) The number of tuples in R(X,Y) ⋈ S(Y,Z) can be estimated as follows: The probability of a match between a tuple in R and S is: 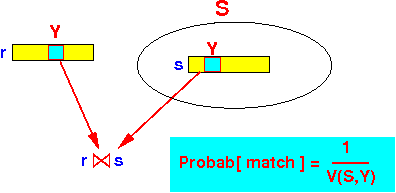There are T(S) tuples in S. Therefore, one tuple r ∈ R will produce this many # of matches: There are T(R) tuples in R. Each tuple r ∈ R produces T(S)/V(S,Y) number of matches (= tuples). Therefore: T(R) × T(S) T( R ⋈ S ) = ----------- V(S,Y)

    ---

    ---

    ---

    ---

  • Conclussion:

    T(R) × T(S) T( R(X,Y) ⋈ S(Y,Z) ) ~= ---------------------- max( V(R,Y), V(S,Y) )

  ---

  ---

  ---

  ---

• Example: estimating the size of a join operation
  • Information on the input relations:

    R(a,b) S(b,c) U(c,d) ======================================================= T(R) = 1000 T(S) = 2000 T(U) = 5000 V(R,b) = 20 V(S,b) = 50 V(S,c) = 100 V(U,c) = 500

    Problem:

    Estimate the size of R ⋈ S ⋈ U

    ---

    ---

  • Method 1: (ordering 1)

    R(a,b) ⋈ S(b,c) ⋈ U(c,d) = ( R(a,b) ⋈ S(b,c) ) ⋈ U(c,d) T(R) × T(S) T( R(a,b) ⋈ S(b,c) ) ~= ---------------------- max( V(R,b), V(S,b) ) 1000 × 2000 ~= --------------- max( 20, 50 ) 2,000,000 ~= ------------ 50 ~= 40,000 ............................ (1) The estimate of the size the join ( R(a,b) ⋈ S(b,c) ) ⋈ U(c,d) is: T( R(a,b) ⋈ S(b,c) ) × T(U) ~= -------------------------------------- max( V(R(a,b) ⋈ S(b,c),c), V(U,c) ) ^^^^^^^^^^^^^^^^^^^^ What is this value ???? From the preservation of value sets assumption, we have: V(R(a,b) ⋈ S(b,c),c) = V(S,c) // V(S,c) = 100 according to data = 100 ...................... (2) Therefore: T( R(a,b) ⋈ S(b,c) ) × T(U) T( R ⋈ S ⋈ U ) ~= ------------------------------------- max( V(R(a,b) ⋈ S(b,c),c), V(U,c) ) 40,000 × 5,000 ~= -------------------- max( 100, 500 ) 200,000,000 ~= ------------- 500 ~= 400,000 ----- answer

    ---

    ---

  • Method 2: (ordering 2)

    R(a,b) ⋈ S(b,c) ⋈ U(c,d) = R(a,b) ⋈ ( S(b,c) ⋈ U(c,d) ) T(S) × T(U) T( S(b,c) ⋈ U(c,d) ) ~= ---------------------- max( V(S,c), V(U,c) ) 2000 × 5000 ~= --------------- max( 100, 500 ) 1,000,000 ~= ------------ 500 ~= 20,000 ............................ (3) The estimate of the size the join R(a,b) ⋈ ( S(b,c) ⋈ U(c,d) ) is: T(R) × T( S(b,c) ⋈ U(c,d) ) ~= -------------------------------------- max( V(R,b), V(S(b,c) ⋈ U(c,d),b) ) ^^^^^^^^^^^^^^^^^^^^ What is this value ??? From the preservation of value sets assumption, we have: V(S(b,c) ⋈ U(c,d),b) = V(S,b ) // V(S,b) = 50 according to data = 50 ...................... (2) Therefore: T(R) × T( S(b,c) ⋈ U(c,d) ) T( R ⋈ S ⋈ U ) ~= ------------------------------------- max( V(R,b), V(S(b,c) ⋈ U(c,d),b) ) 1,000 × 20,000 ~= -------------------- max( 20, 50 ) 20,000,000 ~= ------------- 50 ~= 400,000 ----- answer Note: SAME answer as Method 1 !!!!

    ---

    ---

  • Postscript

    There is another ordering to compute the join: R(a,b) ⋈ S(b,c) ⋈ U(c,d) = ( R(a,b) ⋈ U(c,d) ) ⋈ S(b,c) We cannot handle the estimation this kind of join yet, because: The second join: ( R(a,b) ⋈ U(c,d) ) ⋈ S(b,c) ^^^^ uses two join conditions (namely: R.b = S.b AND U.c = S.c) !!!