- In this webpage, we will study a
classic computer algorithm
that is used to
sort an array
The algorithm is called selection sort
Wikipedia has a nice write up on this algorithm: click here
- We will sort an
array of double in
our
programming example
The selection sort algorithm can be used to sort any data set where there is an ordering among the data items.
- Example problem:
- You are given the following 5 numbers:
6.4 2.5 1.2 2.2 1.1
- Sort the number in ascending order.
I.e., form the following sequence:
1.1 1.2 2.2 2.5 6.4
- You are given the following 5 numbers:
- Overview of the Selection Sort algorithm:
- Find the minimum value
in the list of number
- Swap the
minimum value with the
value in the first position
Illustration:
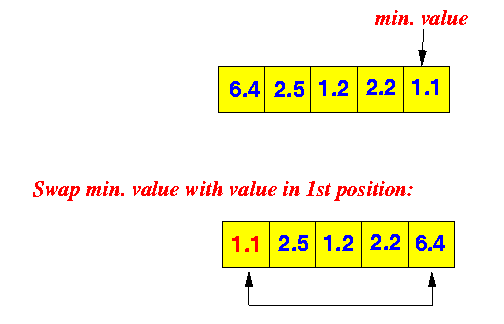
We know that the first element is in its rightful (correct) position.
- Repeat the steps above
for the remainder of the list
(starting at the
second position and
advancing each time)
Step 2:
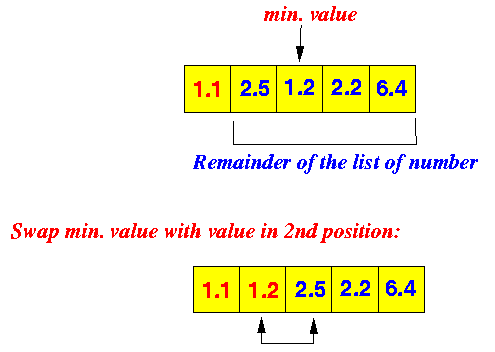
We know that the first and second elements are in their rightful (correct) position.
Step 3:
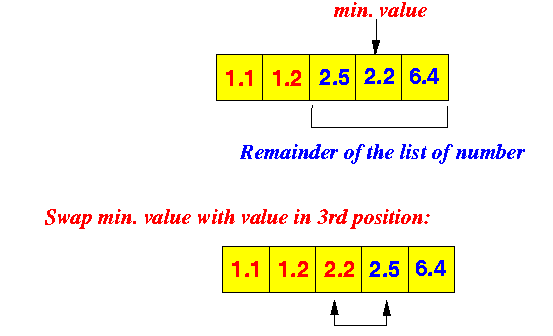
Now we are certain that the first 3 numbers are in the correct order.
And so on...
- Find the minimum value
in the list of number
- Pseudo code of the Selection Sort algorithm:
Let: a = array containing the values Let: n = # of elements 1. Find the array element with the min. value among a[0], a[1], ..., a[n-1]; 2. Swap this element with a[0] Illustration: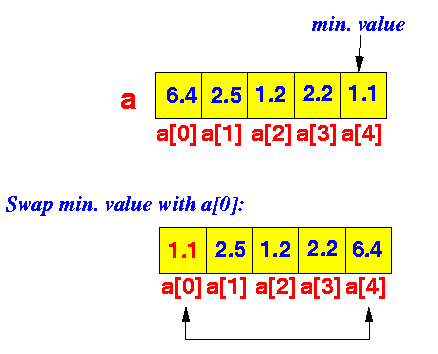
Repeat: 1. Find the array element with the min. value among a[1], ..., a[n-1]; 2. Swap this element with a[1]; Illustration: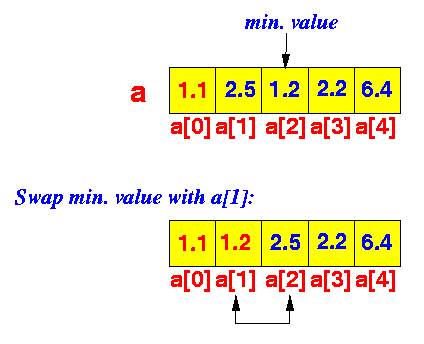 Repeat:
1. Find the array element with the min. value among a[2], ..., a[n-1];
2. Swap this element with a[2];
And so on (until we reach the last element in the array)
Repeat:
1. Find the array element with the min. value among a[2], ..., a[n-1];
2. Swap this element with a[2];
And so on (until we reach the last element in the array)
Observation:
- This formulation of
the algorithm is correct
- But it is not practical --- i.e., it cannot be formulated easily into a computer algorithm
- This formulation of
the algorithm is correct
- We can
re-state (re-formulate)
the previous algorithm using a
for-statement as follows:
Let: the values be store in an array "a" Let: n = a.length for ( i = 0 ; i < n ; i ++ ) { Find the array element with the min. value among a[i], ..., a[n-1]; Swap this element with a[i]; }Check for yourself:
- If i = 0:
Find the array element with the min. value among a[0], ..., a[n-1]; Swap this element with a[0];
- If i = 1:
Find the array element with the min. value among a[1], ..., a[n-1]; Swap this element with a[1];
- And so on !!!
- If i = 0:
- We still need to
work out 2
(smaller) problems:
- Find the array element with the
min. value
among a[i], ..., a[n-1]
(for some given value i)
- Swap two array elements
- Find the array element with the
min. value
among a[i], ..., a[n-1]
(for some given value i)
- Problem statement:
- Given the array elements
a[i], a[i+1], ..., a[n-1]
(n = a.length):
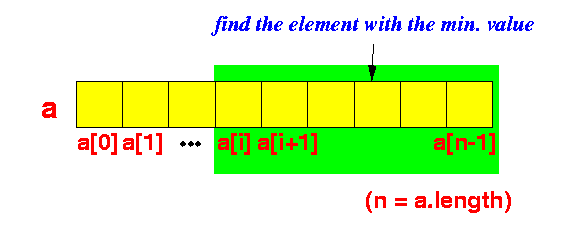
Find the array element with the minimum value among the array elements a[i], a[i+1], ..., a[n-1]
- Given the array elements
a[i], a[i+1], ..., a[n-1]
(n = a.length):
- Previous, we have studied an
algorithm to
find the
array element
containing the minimum value
of all the values
store in the array:
// Find array element with min. value among a[0], a[1], ..., a[n-1] min_j = 0; // Assume elem 0 (a[0]) is the minimum for ( j = 1 ; j < a.length ; j++ ) { if ( a[i] < a[min_j] ) { min_j = j; // We found a smaller minimum, update min_j } }See: click here
- The above algorithm can be
modified to find:
- the array element containing the minimum value among a[i], a[i+1], ..., a[n-1] (n = a.length):
by starting the serach at the array element a[i].
// Find array element with min. value among a[i], a[i+1], ..., a[n-1] min_j = i; // Assume elem i (a[i]) is the minimum for ( j = i+1 ; j < a.length ; j++ ) { if ( a[j] < a[min_j] ) { min_j = j; // We found a smaller minimum, update min_i } } // Result: min_j = index of array element with min. value among a[i] ... a[n-1]Note:
- We must avoid using the variable name i (I used j) because the variable name i is already used in the formulation of the algorithm!!!
- We can now
refine
the Selection Sort algorithm.
Previously, we have (see: click here )
Let the values be store in an array "a" Let n = a.length for ( i = 0 ; i < n ; i ++ ) { 1. Find the array element with the min. value among a[i], ..., a[n-1]; 2. Swap this element with a[i]; }We have just develop an algorithm to solve subproblem 1.
Insert the algorithm and we obtain a more refined (more detailed) algorithm:
Let the values be store in an array "a" Let n = a.length for ( i = 0 ; i < n ; i ++ ) { // Find array element with min. value among a[i], a[i+1], ..., a[n-1] min_j = i; // Assume elem i (a[i]) is the minimum for ( j = i+1 ; j < a.length ; j++ ) { if ( a[j] < a[min_j] ) { min_j = j; // We found a smaller minimum, update min_j } } // Result: min_j = index of array element with min. value among a[i] ... a[n-1] 2. Swap this element (= a[min_j] !) with a[i]; }OK, one subproblem down, one more to go...
- A note on algorithm development:
- While we are developing an
algorithm, we can
introduce new variables
when we see the need for them.
- We just have to make sure that we define every variable when we write the algorithm in Java.
- While we are developing an
algorithm, we can
introduce new variables
when we see the need for them.
- Problem statement:
- Given the array elements
a[i], a[i+1], ..., a[n-1]
(n = a.length) and
a[min_j] has the
minimum value
among
a[i], a[i+1], ..., a[n-1]:
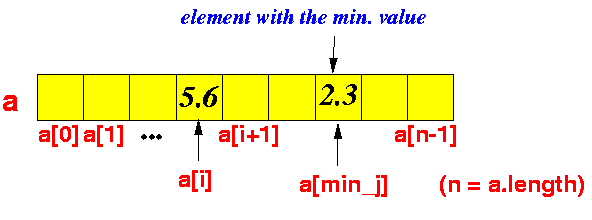
Swap the elements a[i] and a[min_j]:
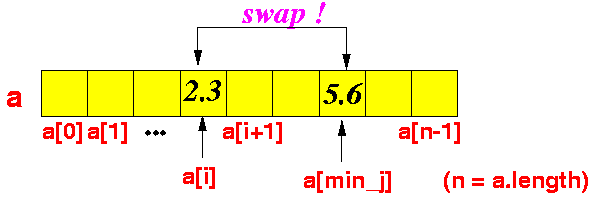
- Given the array elements
a[i], a[i+1], ..., a[n-1]
(n = a.length) and
a[min_j] has the
minimum value
among
a[i], a[i+1], ..., a[n-1]:
- Solution: the 3-way exchange algorithm
- The swap problem illustrated:
- Imagine you have
2 cups named
A and
B and
each cup contains
some liquids
(different kinds of liquid in different cups):
- We want to
swap the
content of the
2 cups:
- Imagine you have
2 cups named
A and
B and
each cup contains
some liquids
(different kinds of liquid in different cups):
- The 3-way exchange algorithm:
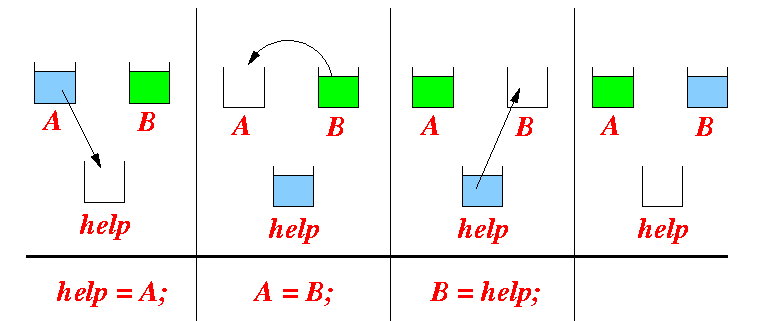
Explanation: we need a helper cup...
- Pour cup A into
the help cup
(this will free up cup A)
- The corresponding program statement is help = A; which will put "(pour)" the value in variable A into the variable help)
- Pour cup B into
cup A
(now cup A has the
correct content and
it will free up cup B)
- The corresponding program statement is A = B; which will put "(pour)" the value in variable B into the variable A)
- Finally,
pour the help cup into
cup B
(now cup B
also has the
correct content)
- The corresponding program statement is B = help; which will put "(pour)" the value in variable help into the variable B)
- Pour cup A into
the help cup
(this will free up cup A)
- The swap problem illustrated:
- Example: 3 way exchange
Suppose the starting values are: A = 3.4 B = 5.6 3 way exchange algorithm: help = A; ----> A = 3.4 B = 5.6 help = 3.4 A = B; ----> A = 5.6 B = 5.6 help = 3.4 B = help; ----> A = 5.6 B = 3.4 help = 3.4
Before the 3 way exchange algorithm: A = 3.4 B = 5.6 After the 3 way exchange algorithm: A = 5.6 B = 3.4
- Swapping the
array elements
a[i] and
a[min_j]:
help = a[i]; a[i] = a[min_j]; a[min_j] = help;
- We can now
refine
the Selection Sort algorithm
further.
Previously, we have (see: click here )
Let the values be store in an array "a" Let n = a.length for ( i = 0 ; i < n ; i ++ ) { // Find array element with min. value among a[i], a[i+1], ..., a[n-1] min_j = i; // Assume elem i (a[i]) is the minimum for ( j = i+1 ; j < a.length ; j++ ) { if ( a[j] < a[min_j] ) { min_j = j; // We found a smaller minimum, update min_j } } // Result: min_j = index of array element with min. value among a[i] ... a[n-1] 2. Swap this element (= a[min_j] !) with a[i]; }We have just develop an algorithm to solve subproblem 2.
Insert the algorithm and we obtain a even more refined algorithm:
Let the values be store in an array "a" Let n = a.length for ( i = 0 ; i < n ; i ++ ) { // Find array element with min. value among a[i], a[i+1], ..., a[n-1] min_j = i; // Assume elem i (a[i]) is the minimum for ( j = i+1 ; j < a.length ; j++ ) { if ( a[j] < a[min_j] ) { min_j = j; // We found a smaller minimum, update min_j } } // Swap a[i] and a[min_j] help = a[i]; a[i] = a[min_j]; a[min_j] = help; }
- If you examine the
algorithm:
Let the values be store in an array "a" Let n = a.length for ( i = 0 ; i < n ; i ++ ) { // Find array element with min. value among a[i], a[i+1], ..., a[n-1] min_j = i; // Assume elem i (a[i]) is the minimum for ( j = i+1 ; j < a.length ; j++ ) { if ( a[j] < a[min_j] ) { min_j = j; // We found a smaller minimum, update min_j } } // Swap a[i] and a[min_j] help = a[i]; a[i] = a[min_j]; a[min_j] = help; }You will determine that we have used the following variables inside the algorithm:
a = the array - type: double[] (we use numbers in the example) i = array index - type: integer j = another array index - type: integer min_j = another array index - type: integer help = stores an array value - type: double (same type as an element of array "a") Note: a[i] is not a new variable a[min_j] is not a new variable
- Selection Sort Algorithm in Java:
public class SelSort1 { public static void main(String[] args) { /* ----------------------------------------------------------------- Define the used variables (make sure you have the type correct !) ----------------------------------------------------------------- */ double[] a = { 6.7, 2.3, 7.8, 3.4, 5.6, 4.5, 8.9 }; // 7 elements int i, j, min_j; // Array indices double help; // helper variable for 3-way exchange /* --------------------------------------------------- The selection sort algorithm --------------------------------------------------- */ for ( i = 0 ; i < a.length ; i ++ ) { /* --------------------------------------------------- Find array element with min. value among a[i], a[i+1], ..., a[n-1] --------------------------------------------------- */ min_j = i; // Assume elem i (a[i]) is the minimum for ( j = i+1 ; j < a.length ; j++ ) { if ( a[j] < a[min_j] ) { min_j = j; // We found a smaller minimum, update min_j } } /* --------------------------------------------------- Swap a[i] and a[min_j] --------------------------------------------------- */ help = a[i]; a[i] = a[min_j]; a[min_j] = help; } } }
- Example Program:
(Demo above code)

- Prog file: click here
How to run the program:
- Right click on link and
save in a scratch directory
- To compile: javac SelSort1.java
- To run: java SelSort1
- You have seen the first
pretty complex algorithm
in this course.
- Notice that:
- If you only look at
the final algorithm:
Let the values be store in an array "a" Let n = a.length for ( i = 0 ; i < n ; i ++ ) { // Find array element with min. value among a[i], a[i+1], ..., a[n-1] min_j = i; // Assume elem i (a[i]) is the minimum for ( j = i+1 ; j < a.length ; j++ ) { if ( a[j] < a[min_j] ) { min_j = j; // We found a smaller minimum, update min_j } } // Swap a[i] and a[min_j] help = a[i]; a[i] = a[min_j]; a[min_j] = help; }the algorithm is pretty confusing and cannot be easily understood !!!
However:
- If you look at the
algorithm with the
bird's eye view:
for ( i = 0 ; i < n ; i ++ ) { Find the array element with the min. value among a[i], ..., a[n-1]; Swap this element with a[i]; }It's quite simple !!!
- If you only look at
the final algorithm:
- Lesson on a computer algorithm is developed:
- Formulate the algorithm
using abstract operations
Examples:
- "Find the array element with the min. value among a[i], ..., a[n-1];"
- "Swap this element with a[i];"
- Refine (flesh out) the
abstract steps.
I.e., make the abstract steps more concrete
Note:
- Ideally, you would
only use
computer statement to
describe the
concrete steps
- But sometimes, you may need to use
other
(more simpler) abstract steps
in the description.
These (more simpler) abstract steps will need to be refined
- So the process of refining can
take several cycles
We call this technique: "step-wise refinement"
- Ideally, you would
only use
computer statement to
describe the
concrete steps
We will use the "step-wise refinement" technique later in the course when we discuss the topic "Modular programming using the top-down design methodology".
- Formulate the algorithm
using abstract operations