- Definition:
cost of k-medians
- Given an instance (S,k)
of k-median problem, where
- k = an integer - number of medians
- S = set of n data points
with a distance metric d(-,-)
- The cost of the
k-medians
C1, C2, ..., Ck is:
-
f(S, C1, C2, ..., Ck) =
∑x ∈ S
(
mini = 1, 2, ..., k d(x, Ci)
)
-
f(S, C1, C2, ..., Ck) =
∑x ∈ S
(
mini = 1, 2, ..., k d(x, Ci)
)
- Given an instance (S,k)
of k-median problem, where
- Continuous clustering:
- In continuous clustering, the cluster centers need not be data points in the input stream
- Discrete clustering:
- In discrete clustering, the cluster centers must be data points in the input stream
- Definition:
cost(S,Q)
- Cost(S,Q) = the smallest possible cost if the medians are required to belong to the set Q
Cost of continuous clustering:
- Cost of the continuous clustering problem =
cost(S, Rd)
where d = space spanned by the attributes
Cost of discrete clustering:
- Cost of the discrete clustering problem =
cost(S, S)
where d = space spanned by the attributes
- The problem of clustering
on input data from a stream is
also handled by
partitioning
- First, the authors present a
clustering algorithm
that has
very small space requirement:
- Divides the input data into
pieces (segments)
- Cluster each piece
separately
- Then cluster all the centers of the resulting clusters in one batch
This algorithm is called Small-Space in the paper.
- Divides the input data into
pieces (segments)
- Next they presents an
incremental center clustering
algorithm:
- Divides the input data into
pieces (segments)
- Cluster each piece
separately
- Cluster the centers of the resulting clusters incrementally
This algorithm is called Smaller-Space in the paper
- Divides the input data into
pieces (segments)
- Description of the Small-Space (S) Algorithm:
- Divide input stream into
m disjoin pieces
X1,
X2,
...,
Xm
Example:
- For each Xi
(i = 1, 2, ..., m),
find O(k) centers (cluster centroids)
in Xi
(So we form O(k) clusters)
Example:
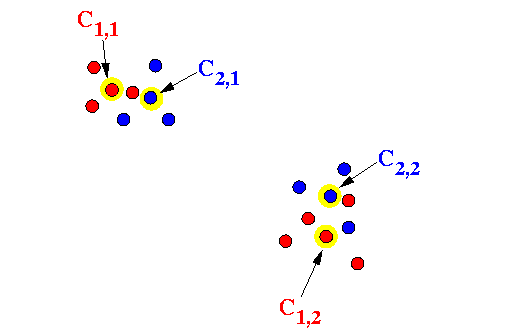
There will be O(k×m) centers total
- Let X' be the
O(k×m) centers
obtained in step 2
Weight each center by the number of points in its cluster
- Cluster
X' to obtain
k centers
The weighted centers are computed by using:
- c1 = ∑Yj ∈ X' ( wj1×yj1 ) / |W|
- c2 = ∑Yj ∈ X' ( wj2×yj2 ) / |W|
- And so on...
- Divide input stream into
m disjoin pieces
X1,
X2,
...,
Xm
- Before analyzing the
Small-Space algorithm,
we need to some
relationships
between the
discrete and
the continuous
clustering problem.
- Theorem 1
- Given an instance of the
k-median problem
(S, k)
- Then:
- For any set Q: cost(S, S) ≤ 2 × cost(S, Q)
- Note: the intention is that Q is a larger set than S so there is more possibilities to pick better centers...
Proof:
- Consider the k-median solution
with centroids restricted to
data points in Q:

The cost of this solution is:
- Cost(S, Q) = ∑x ∈ S ( mini = 1, 2, ..., k d(x, Ci) )
- Now replace
each centroids
with the nearest data point
in the cluster:
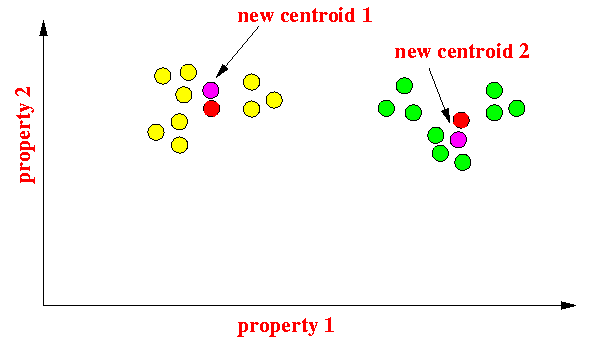
The cost of this solution is:
-
Cost(S, S) =
∑x ∈ S
(
mini = 1, 2, ..., k d(x, C'i)
)
with C'i ∈ S i = 1, 2, ..., k
The distance d(x, C'i) can be bounded by:
- d(x, C'i) ≤ 2×d(x, Ci)
because:

-
Cost(S, S) =
∑x ∈ S
(
mini = 1, 2, ..., k d(x, C'i)
)
- Therefore:
Cost(S, S) = ∑x ∈ S ( mini = 1, 2, ..., k d(x, C'i) ) ≤ 2 × ∑x ∈ S ( mini = 1, 2, ..., k d(x, Ci) ) = 2 × Cost(S, Q)
- Given an instance of the
k-median problem
(S, k)
- Theorem 2
- Consider an arbitrary partition
of the input data S
into
m sets:
-
X1,
X2, ...,
Xm
- Then:
-
&sum i = 1, 2, .. , m
Cost(Xi, Xi)
≤
2×Cost(S, S)
where:
- Cost(Xi, Xi) is the cost of a k-median problem
- Cost(S, S) is the cost of a (k×m)-median problem
-
&sum i = 1, 2, .. , m
Cost(Xi, Xi)
≤
2×Cost(S, S)
Proof:
- From Theorem 1:
-
Cost(Xi, Xi)
≤
2×Cost(Xi, S)
for i = 1, 2, .. , m
-
Cost(Xi, Xi)
≤
2×Cost(Xi, S)
for i = 1, 2, .. , m
- Therefore:
-
&sum i = 1, 2, .. , m
Cost(Xi, Xi)
≤
2 × (
Cost(X1, S) + Cost(X2, S) + ... +
Cost(Xk, S) )
= 2 × Cost(S,S)
We will use k×m medians in X1, X2, ..., Xm for Cost(S,S)...
-
&sum i = 1, 2, .. , m
Cost(Xi, Xi)
≤
2 × (
Cost(X1, S) + Cost(X2, S) + ... +
Cost(Xk, S) )
- Consider an arbitrary partition
of the input data S
into
m sets:
- Let us review the
Small-Space Algorithm:
- Divide input stream into
m disjoin pieces
X1,
X2,
...,
Xm
- For each Xi
(i = 1, 2, ..., m),
find O(k) centers (cluster centroids)
in Xi
(So we form O(k) clusters per set Xi)
There will be O(k×m) centers total
Theorem 1 and 2 relate to the cost of the solution at this point in the algorithm
- Let X' be the
O(k×m) centers
obtained in step 2
Weight each center by the number of points in its cluster
- Cluster
X' to obtain
k centers
- Divide input stream into
m disjoin pieces
X1,
X2,
...,
Xm
- The next theorem will bound the cost of clustering the cluster centers ....
- Theorem 3:
- Let:
-
C =
&sumi = 1, 2, .., m
cost(Xi, Xi)
(I.e., C is the sum of cost of the partitioned solutions)
Example:

-
C* = Cost(S,S) =
&sumi = 1, 2, .., m
cost(Xi, S)
(I.e., C* is the cost of the solution of the complete problem)
Example:
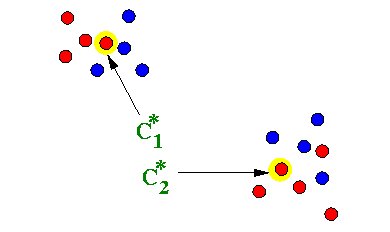
-
C =
&sumi = 1, 2, .., m
cost(Xi, Xi)
- And let:
- Let X*
be a weighted instance
of the k-median problem
solved by the Small-Space
algorithm
by clustering the clusters

The cost of this solution is: f(X*, X*)
(because after clustering the data items, we only know the locations of the cluster centers)
Claim:
- The Small Space algorithm produces a k-median solution with a cost of at most 2×(C + C*)
- Let X*
be a weighted instance
of the k-median problem
solved by the Small-Space
algorithm
by clustering the clusters
Proof:
- Let:
-
Ci,1,
Ci,2, ...,
Ci,k
be the centroids (medians)
that achieve the
minimum cost
cost(Xi, Xi),
for i = 1, 2, ..., m
- C*1, C*2, ..., C*k be the centroids (medians) that achieve the minimum cost cost(S, S)
-
Ci,1,
Ci,2, ...,
Ci,k
be the centroids (medians)
that achieve the
minimum cost
cost(Xi, Xi),
for i = 1, 2, ..., m
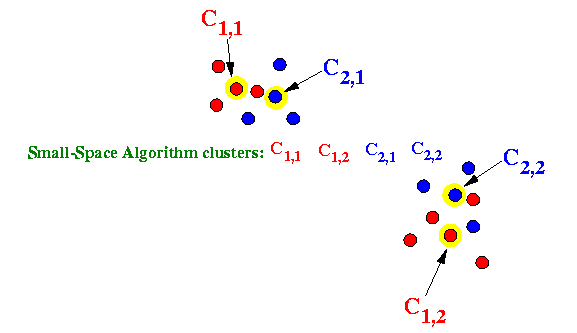
- The following picture tries to make it
less abstract:
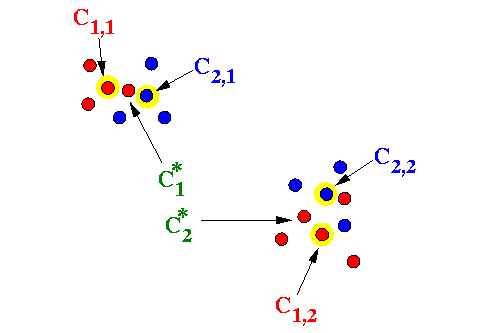
The red dots are elements in X1
The blue dots are elements in X2
All dots are elements in S
- We do not need to compute
the cost expression exactly:
- f(X*, X*)
We will instead bound this expression using Theorem 1
- In order to use Theorem 1,
we first compute
the cost of the
set of weighted centers X*
restricted to these point as centers:
C*1,
C*2, ...,
C*k:
-
f(X*,
C*1,
C*2, ...,
C*k) =
∑Ci,j ∈ X*
(
minh = 1, 2, ..., k
wi,j
×
d(Ci,j, C*h)
)
......... (1)
- The input set X* consists of the cluster centers Ci,j
- The point C*h is the nearest centroid in the solution f(S, S) that is closest to the cluster centers Ci,j (because we minimize over C*1, C*2, ..., C*k )
- wi,j = number of elements x ∈ Xi associated with the center Ci,j (= the weight of the centroid Ci,j in Xi)
-
f(X*,
C*1,
C*2, ...,
C*k) =
∑Ci,j ∈ X*
(
minh = 1, 2, ..., k
wi,j
×
d(Ci,j, C*h)
)
......... (1)
- Define these notations to simplify
the expression:
- c(x) =
the closest of
Ci,1,
Ci,2, ...,
Ci,k
to element x,
for x ∈ Xi
(I.e., c(x) is the center associated with the data point x in the restricted set Xi) - C*(x) =
the closest of
C*1,
C*2, ...,
C*k
to element x
(I.e., C*(x) is the center associated with the data point x in the full set S)
Example:
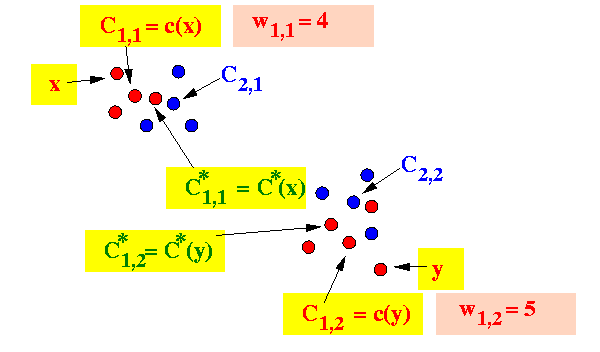
Using these 2 definitions, Equation 1 can be re-written as:
- The original Equation (1):
-
f(X*,
C*1,
C*2, ...,
C*k) =
∑Ci,j ∈ X*
(
minh = 1, 2, ..., k
wi,j
×
d(Ci,j, C*h)
)
......... (1)
- Re-written as:
-
f(X*,
C*1,
C*2, ...,
C*k) =
∑Ci,j ∈ X*
(
{x: c(x) = Ci,j}
wi,j
× d(c(x), C*(x))
)
......... (2)
- c(x) =
the closest of
Ci,1,
Ci,2, ...,
Ci,k
to element x,
for x ∈ Xi
- Fact (triangle inequality)
- d(c(x), C*(x)) ≤ d(x, c(x)) + d(x, C*(x))
Hence:
- {x: c(x) = Ci,j} wi,j × d(c(x), C*(x)) ≤ ∑ {x: c(x) = Ci,j} ( d(x, c(x)) + d(x, C*(x)) )
Therefore:
-
f(X*,
C*1,
C*2, ...,
C*k)
≤
∑Ci,j ∈ X*
(
∑ {x: c(x) = Ci,j}
(
d(x, c(x))
+
d(x, C*(x))
)
)
When you sum all elements belong to all centers, we are actually summing all elements in the original set
Se we can replace: "∑Ci,j ∈ X* ( ∑ {x: c(x) = Ci,j} ... )" by: ∑ {x ∈ S}
= ∑ {x ∈ S} ( d(x, c(x)) + d(x, C*(x)) )
= ∑ {x ∈ S} d(x, c(x)) + ∑ {x ∈ S} d(x, C*(x))
- c(x) =
the closest of
Ci,1,
Ci,2, ...,
Ci,k
to element x,
for x ∈ Xi
(I.e., c(x) is the center associated with the data point x in the restricted set Xi) - C*(x) =
the closest of
C*1,
C*2, ...,
C*k
to element x
(I.e., C*(x) is the center associated with the data point x in the full set S) - f(X*, C*1, C*2, ..., C*k) ≤ C + C* ................ (3)
Since:
We have that:
-
∑ {x ∈ S}
d(x, c(x))
= cost of solution using partitioned sets
= C
∑ {x ∈ S} d(x, C*(x)) = cost of solution using complete set = C*
Therefore:
- Now we can apply
Theorem 1:
-
f(X*, X*)
≤
2 × f(X*,
C*1,
C*2, ...,
C*k)
(the set Q is
{C*1,
C*2, ...,
C*k}
)
= 2(C + C*)
-
f(X*, X*)
≤
2 × f(X*,
C*1,
C*2, ...,
C*k)
(the set Q is
{C*1,
C*2, ...,
C*k}
)
- Let:
- The paper also presents an
approximate clustering step
that uses an approximation algorithm
presented in another literature
- I have omitted this step to save time
- Algorithm
Smaller-Space( S, i ) { if ( i == 0 ) { stop; // Done } Divide S into k disjoint pieces: X1, X2, ..., Xk Cluster each Xi; Let X* = set of k×m cluster centers; Call Smaller-Space( X*, i-1 ); }
- Example:
- Input data

- Partition into k-sets:
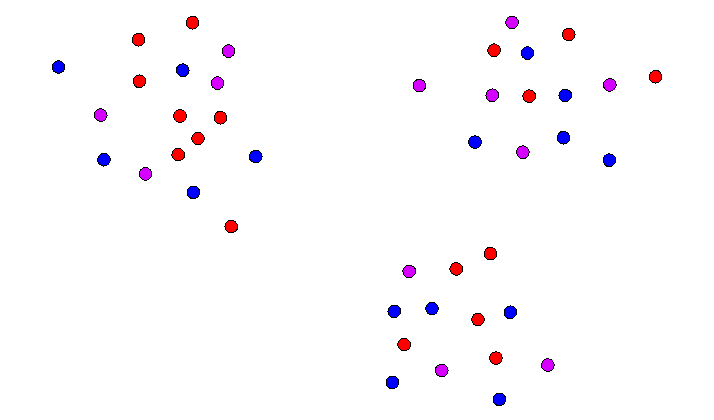
- Determinte the cluster centers:
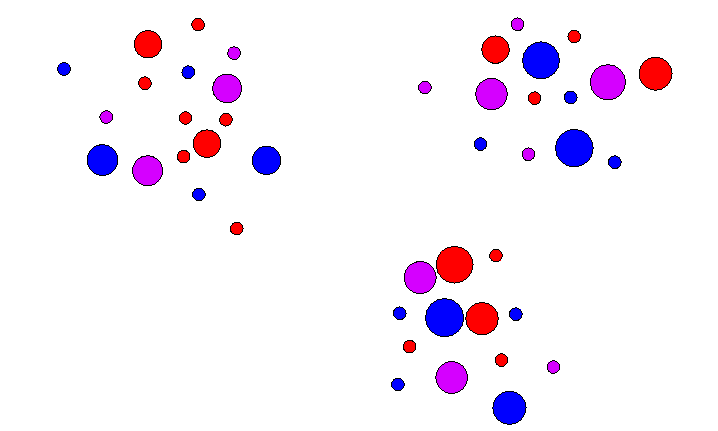
- Repeat with cluster center as input data:
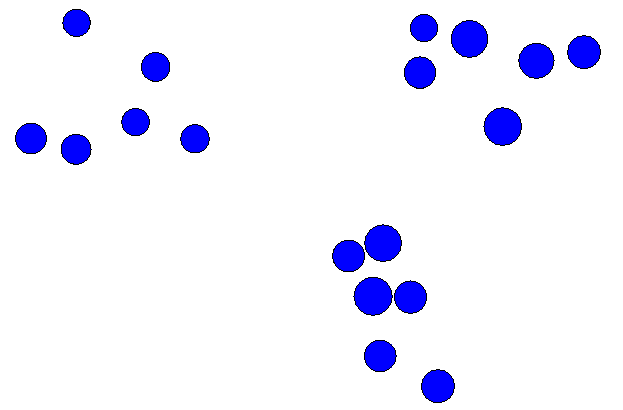
- Input data
- The approach is similar
to the Smaller-Space
algorithm
- Stream clustering algorithm:
- Input the first m data points
(m is a user parameter)
- Cluster the
m data points into
2k
level 1 cluster centers
- Repeat the above steps until we have processed
m2/(2k) data points
We will now have m/(2k) × 2k = m level 1 cluster centers
- Cluster these
m
level 1 cluster centers
into 2k level 2 cluster centers
And so on...
- In general:
- Maintain < m
level-i cluster centers
- When there are m level-i cluster centers, immediately generate 2k level-(i+1) centers
- Maintain < m
level-i cluster centers
- At the end of the stream, cluster all centers into k final centers
Graphically:
- Cluster first m data points:

- Then the next m data points:

- Until you have m cluster points:

- Cluster the m cluster points
into 2k level 2 cluster points:

- Repeat,
next m data points:
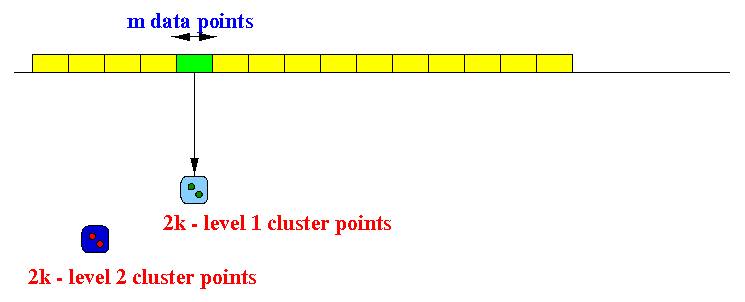
- And so on...
- Input the first m data points
- I have left out
the error analysis
because I omitted
a compression step
in their algorithm.
This compression step refers to another publication that we did not discuss.
- As a result, the error expression does not make any sense if I present them verbatim.