- Recall that
Geenwald and Khanna's summary
has the following form:
-
{(v0, g0, Δ0),
(v1, g1, Δ1), ...,
(vk, gs-1, Δs-1)}
Or the alternate form:
{ (v0, rmin(v0), rmin(v1)), (v1, rmin(v1), rmin(v1)), ..., (vs−1, rmin(vs−1), rmin(vs−1)) }
- Property of the summary:
- r − εN ≤ answer(r) ≤ r + εN
- r = actual rank of the item i
- answer(r) = rank of the answer obtained from the ε-approximate quantile summary for the item at rank r
- N = number of items in the quantile summary
-
{(v0, g0, Δ0),
(v1, g1, Δ1), ...,
(vk, gs-1, Δs-1)}
- When applying Arasu's algorithm
to construct
ε-approximate frequency count
summary
for a window,
run
Greenwald and Khanna's algorithm
with error parameter:
- εi / 2 !!! (see: click here)
Where:
2L 1 εi = ---- × -------- × ε (see: click here) 2i 4(L+1)
- Algorithm:
Let B1, B2, ..., Bs be the best active blocks that covers the current window Let A1, A2, ..., As be their Quantile summaries Let ε1, ε2, ..., εs be their error parameters
/* ------------------------------------------- Extract a quantile summary from each Ai ------------------------------------------- */ for ( k = 1; k ≤ s; k++ ) { Qk = ∅; // This is the extracted quantile summary w = εkNk; // The weight of an entry in Qk for ( i = εk, 2εk, 3εk, ..., 1 ) { e = { QuanQuery(Ak, i×Nk) }; Qk = Qk ∪ {(e, w)}; } // At this point, Qk consists of 1/εk and // Qk is a εk-approximate quantile summary for Bk // Each element in Qk is given a weight of εkNk } /* -------------------------------------------------------- Construct a quantile summary for the (sliding) window -------------------------------------------------------- */ Q = ∅; // Q is the quantile summary for window for ( k = 1; i ≤ s; k++ ) Q = Q ∪ Qk; Sort(Q'); - NOTE:
- It is a bit complicated
to use the window quantile summary
- How to use the window quantile summary is detailed in the next algorithm
- It is a bit complicated
to use the window quantile summary
- Using the sliding window quantile summary:
/* ------------------------------------------------------------------- QuantileQuery(Q, φ): look up the element at rank φN Q = window quantil constructed with the above algorithm NQ = N1 + N2 + ... + Ns φ = value between 0 and 1 ------------------------------------------------------------------- */ value QuantileQuery( ArasuQuantile Q, rank φ ) { /* ------------------------------------------------- NOTE: 1. Q is sorted !!! 2. each element in Q is assigned a weight ------------------------------------------------- */ find the element ek ∈ Q such that: 1. w1 + w2 + ... + wk-1 < φ(N1 + N2 + ... + Ns) 2. w1 + w2 + ... + wk-1 + wk ≥ φ(N1 + N2 + ... + Ns) return(ek); }
- Claim:
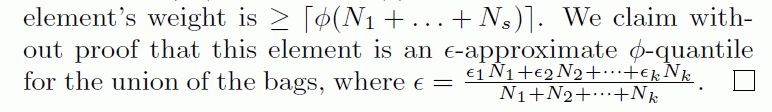
- Theorem 2:
