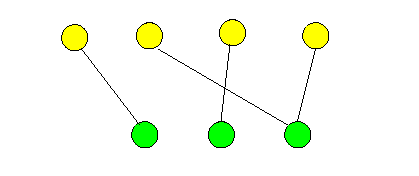
- Bipartite graphs
- A bipartite graph is a graph whose vertices are decomposed into two disjoint sets such that no two graph vertices within the same set are connected by an edge
Example:
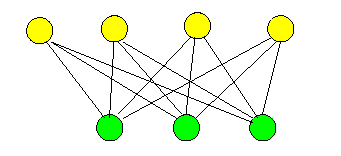
- Complete Bipartite graph
- A complete bipartite graph is a bipartite graph such that every pair of graph vertices in the two sets are adjacent (connected by an edge).
Example:
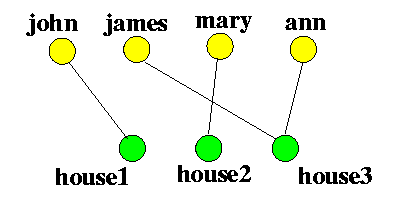
- The terms lattice graph,
(mesh graph, or grid graph) refers to
a category of graphs
whose drawing corresponds
to some grid/mesh/lattice.
Specifically:
- its vertices
correspond to the nodes of the mesh
and
- its edges correspond to the ties between the nodes.
Example:
- its vertices
correspond to the nodes of the mesh
and
- A lattice graph L(m,n) is also known the line graph of the complete bipartite graph K(m,n)
- A lattice structure can be used
to enumerate
the list of all possible subsets
- Example: all subset of
{a,b,c,d}
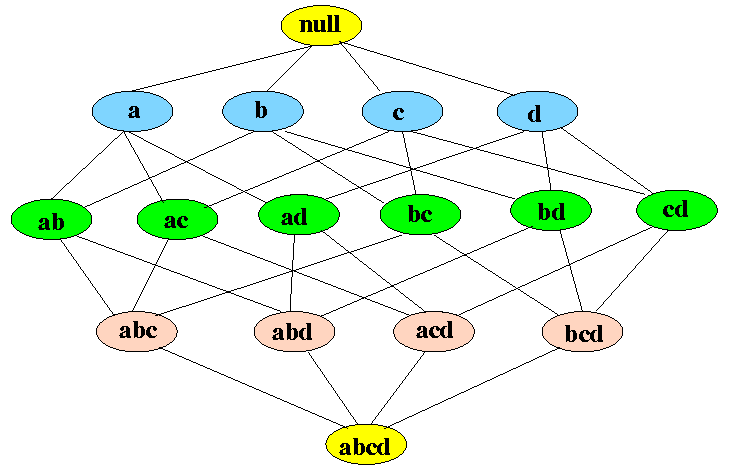
- There are 2k - 1 non-empty subsets of a k-item set
- Approaches:
- Reduce the number of
candidate itemsets
The Apriori principle is an effective way to eliminate some of the candidate sets early in the generation process
- Reduce the number of
comparision operations
Normally: check if an item set is contained in a transaction
You can use a lattice-like data structure to reduce the number of comparisons
- Reduce the number of
candidate itemsets
- Apriori Principle
- If an itemset x
is frequent
(i.e., freq(x) ≥
θN),
then:
-
all subsets of x
is also
frequent
Example: if {b,c,d} is frequent, then all subsets of {b,c,d} are also frequent
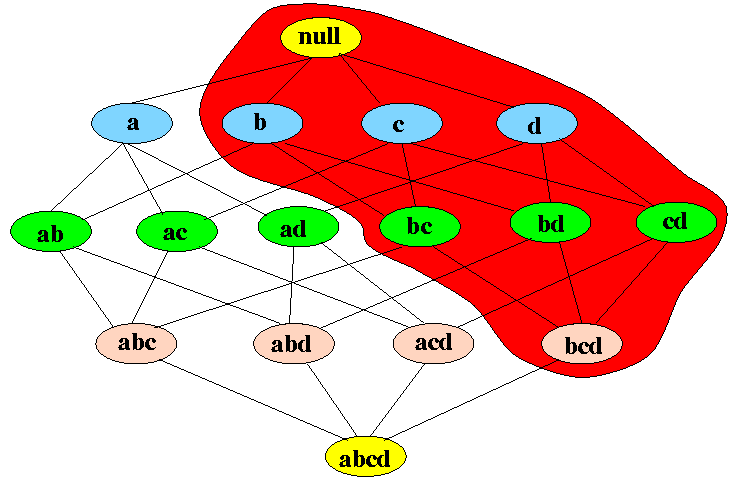
- If an itemset x
is frequent
(i.e., freq(x) ≥
θN),
then:
- Converse of the Apriori Principle:
- If an itemset x
is not frequent
(i.e., freq(x) <
θN),
then:
-
all super sets of x
are
not frequent
Example: if {a,b} is infrequent, then all its super sets ({a,b,c}, {a,b,d}, and {a,b,c,d}) are also infrequent:
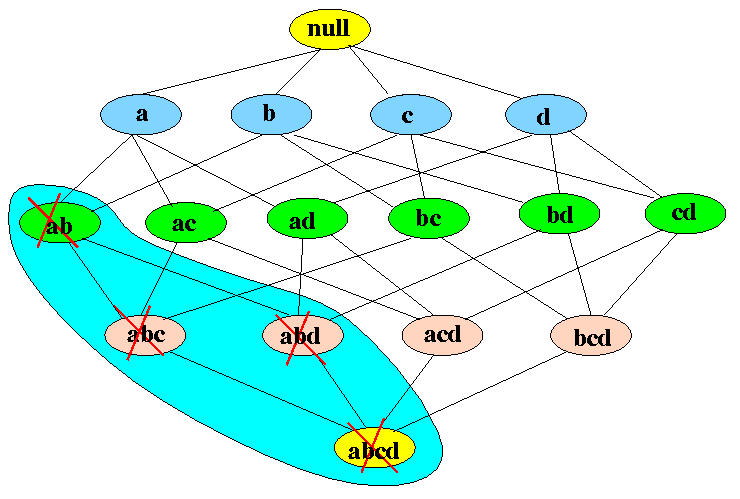
- If an itemset x
is not frequent
(i.e., freq(x) <
θN),
then:
- Conclusion:
- If a node x is infrequent, the entire subgraph rooted at x can be pruned away from the candidate set
This technique is known as support-based pruning
- The Apriori Algorithm
is an off-line algorithm
to find
frequent itemsets
It was first describe in the paper: click here
-
It is now an industry standard:
click here
It is available on Oracle: click here
- Example of Apriori: min. support =
60%
- Transactions:
- Bread, Milk
- Bread, Diapers, Beer, Eggs
- Milk, Diapers, Beer, Coke
- Bread, Milk, Diapers, Beer
- Bread, Milk, Diapers, Coke
- 1-item candidate sets:
- Form all possible 1-item sets
- Find their support
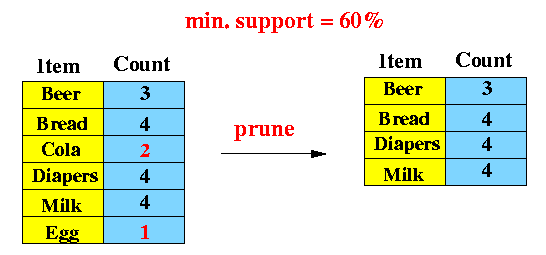
- 2-item candidate sets:
- Form all possible 2-item sets using only 1-item sets with sufficient support
- Find their support
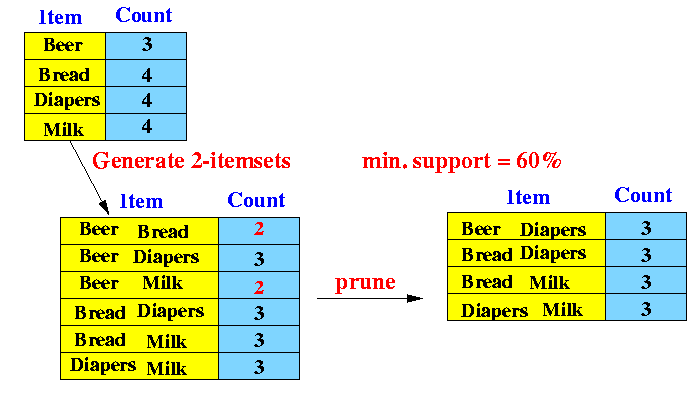
- 3-item candidate sets:
- Form all possible 3-item sets using only 2-item sets with sufficient support
- Find their support
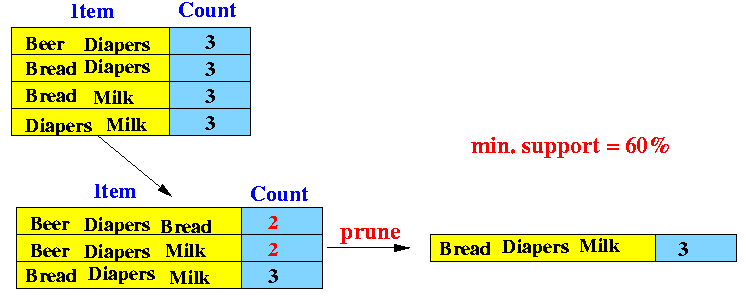
- Transactions:
- The Apriori Algorithm:
k = 1; F(1) = { i | freq(i) ≥ θN }; // 1-item sets repeat { k = k + 1; /* ---------------------------------- Candidate set generation ---------------------------------- */ C(k) = Apriori-Gen( F(k-1) ); // Generate candidate itemsets // using only itemsets in F(k-1) /* -------------------------------------------------- Compute support for candidate sets -------------------------------------------------- */ for ( each candidate set c ∈ C(k) ) do Freq(c) = 0; for ( each transaction t ∈ T ) do { for ( each candidate set c ∈ C(k) ) do { if ( c ∈ t ) Freq(c)++; } } /* --------------------------------------- Prune Candidate set C(k) --------------------------------------- */ F(k) = { c | c ∈ C(k) ∧ Freq(c) ≥ θN } } until F(k) == ∅ Frequent itemsets = F(1) ∪ F(2) ∪ ... ∪ F(k-1)
- The Apriori Algorithm
contains 3 phases
of code:
- C(k) = Apriori-Gen( F(k-1) );
-
Generate the k-item candidate
sets
- Support Counting
-
Find the Freq(c) for
each candidate set c
-
F(k) = { c | c ∈ C(k) ∧ Freq(c) ≥ θN }
-
Prune
the k-item candidate
sets
(There are actually 2 phases: the prune phase is very simple and is ignored from the discussion.)
- C(k) = Apriori-Gen( F(k-1) );
- The steps 1 and 2 will be discussed separatedly next.
- There are 3 proposed
methods to generate
k-items candidate sets
:
- Brute Force
- F(k-1) × F(1) method
- F(k-1) × F(k-1) method
- Brute Force Method
- Generates all sets of size k
Advantage: simple code
Advantage: large number of item sets generated (largest possible number)
- F(k-1) × F(1) method
F(k) = ∅; for ( each S ∈ F(k) ) do for ( each T ∈ F(1) ) do add S ∪ T to F(k);Properties:
- Produces
|F(k)| × |F(1)|
candidate sets
- Generates
duplicate
candidate sets
- The output candidate set can still be large
- Produces
|F(k)| × |F(1)|
candidate sets
- F(k-1) × F(k-1) method
F(k) = ∅; for ( each S ∈ F(k) ) do for ( each T ∈ F(k-1) ) do if ( | S ∪ T | == k ) add S ∪ T to F(k);
- Support counting is
computing the frequency
Freq(S) for
each item set
S
in the candidate set C(k)
(which we have generated
in the previous step)
- There are 2 approaches
in doing this counting:
Method 1: naive comparison
/* ---------------------- Initialize counts ---------------------- */ for ( each item set S ∈ C(k) ) do { Freq(S) = 0; } /* ---------------------------------- Count ---------------------------------- */ for ( each transaction t ) do { for ( each k-item set S ∈ C(k) ) do { if ( S ⊆ t ) { Freq(S)++; } } }
- Graphically:
Transactions: t1 t2 ... t .... | +----------------------+ | Candidate sets C(k): C1 C2 C3 ... Cn | ^ ^ ^ ^ | | | | | | +---+---+--------+-----------+ t ⊆ Ci ? traverse all sets in C(k)Properties:
- Too slow (too many sets
to traverse)
- Need access structures to speed up the access to the counters Freq(S)
Method 2: lookup counting
/* ------------------------------- Initialize counters ------------------------------- */ for ( each item set S ∈ C(k) ) do { Freq(S) = 0; } for ( each transaction t ) do { for ( each k-subset T of t ) do { Lookup T in C(k); if ( found ) { Freq(T)++; } } }
- Too slow (too many sets
to traverse)
- Graphically:
Transactions: t1 t2 ... t .... | +---------------------------+ | k-item sets +--+--+--+--+--+--+ | | | | | | | v v v v v v v T1 T2 T3 T4 T5 T6 T7 | Candidate sets C(k): C1 C2 C3 ... Cn | ^ | | | +--------------------------+ "lookup"There are 2 unspecified parts in the algorithm:
- How to generate k-item sets
from a given set
- How to organize the candidate sets C(k) so we can look up a k-item set
- How to generate k-item sets
from a given set
- Algorithm to generate k-subsets
of a set:
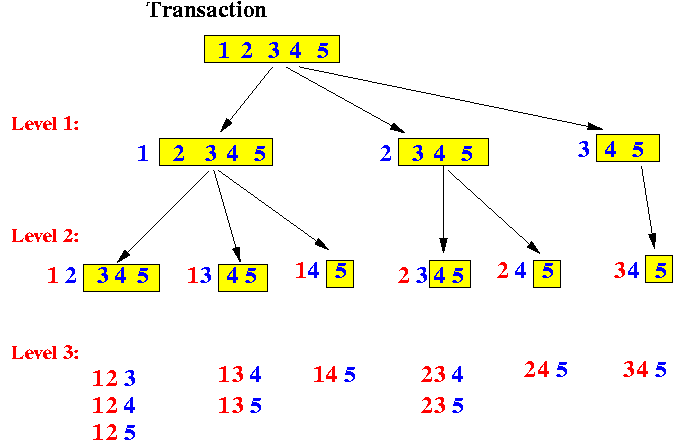
Sample implementation:
/* ----------------------------------------------- gen(head, a, k): generate k-item strings head = prefix of the string a = remaining characters to choose to complete the string k = number of characters to add ----------------------------------------------- */ void gen(char *head, char *a, int k) { char myHead[10]; char *c, *e; /* ------------------------------------ Check if we need to add characters ------------------------------------ */ if ( k == 0 ) { printf(">> %s\n", head); return; // Done } /* ---------------------------------------------------- Copy prefix into local variable to enable recursion ---------------------------------------------------- */ strcpy(myHead, head); for ( e = myHead; *e != '\0'; e++ ); *(e+1) = '\0'; /* ----------------------------------------- Add one character to the prefix string ----------------------------------------- */ for ( c = a; *c != '\0'; c++ ) { *e = *c; // Add next character to prefix gen(myHead, c+1, k-1); // Add remaning characters } }
- Example Program:
(Demo above code)

- Prog file: click here
- Consider the algorithm:
/* ------------------------------- Initialize counters ------------------------------- */ for ( each item set S ∈ C(k) ) do { Freq(S) = 0; } for ( each transaction t ) do { for ( each k-subset T of t ) do { Lookup T in C(k); ********* if ( found ) { Freq(T)++; } } }How can we speedup the look up process to find the counter for C(k) ???
- Standard solution:
- Hashing !
- In the Apriori algorithm,
the counters
for the candidate itemsets
are partitioned
into different buckets
and stored
in a hash tree
- this speeds up the search for an item set
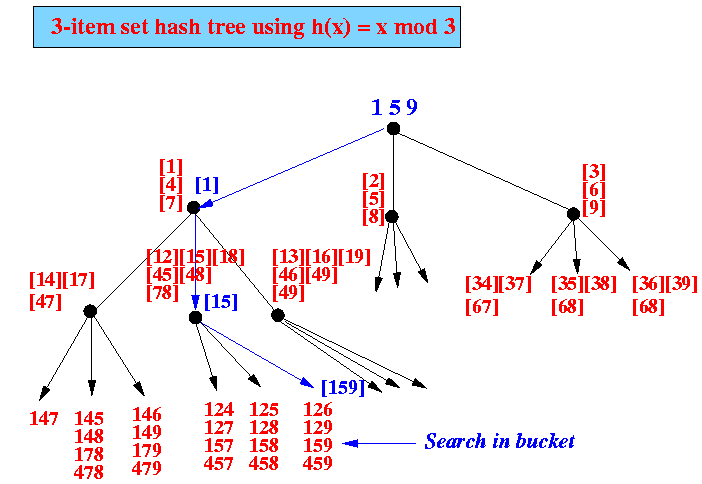
- Example: 3-item hash tree
for transactions containing items 1, 2, 3, 4, 5, 6, 7, 8, 9
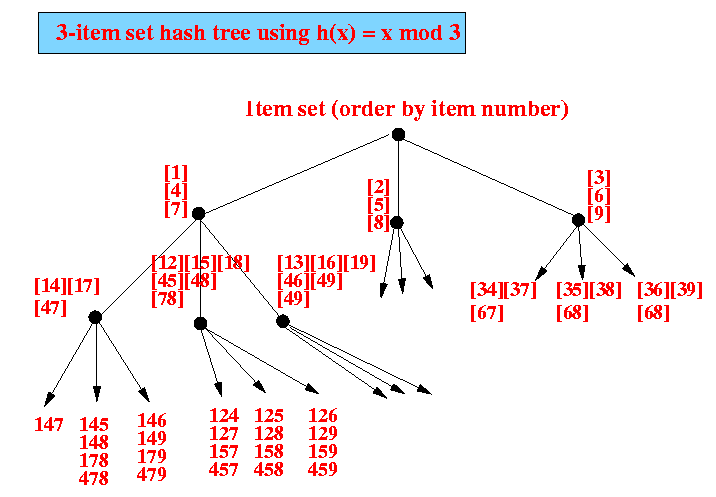
Organization:
- The leaves of the tree
contains the counters
for the different
3-item item sets
- The items in a transaction
is first sorted
- We then form all 3 item itemsets
from the items in the transaction
The 3-item itemset is hashed used hash(x) = x mod 3 to locate the counter for the itemset
- The leaves of the tree
contains the counters
for the different
3-item item sets
- Concrete example: finding
the counter for
itemset 1 5 9