- Notations used in the paper:
- Σ = alphabet with
n symbols
- x =
( x1,
x2, ...
xN)
x is a sequence of values.
Each xi is an element from the alphabet Σ
( x is the input stream)
- N =
number of elements in
the input stream
- fx(a) =
number of occurrences of
a in
x
- θ =
threshold value
(0 ≤ θ ≤ 1)
- Heavy elements:
- I(x, θ) = { a ∈ Σ | fx(a) > θ × N }
- Σ = alphabet with
n symbols
- Lemma 2.1:
- The number of elements that has
frequency
greater than
θN
is
at most 1/θ
I.e.:
- | I(x, θ) | ≤ 1/θ
- The number of elements that has
frequency
greater than
θN
is
at most 1/θ
- Proof:
- If there are
more than 1/θ
elements with
frequency
θN
or more, then there will be
more than
(1/θ) × θN =
N
elements in the stream
But there at only N elements in the stream.
- If there are
more than 1/θ
elements with
frequency
θN
or more, then there will be
more than
(1/θ) × θN =
N
elements in the stream
- Proposed Algorithm:
Variable utilization: K = set of potentially heavy elements count[e] = adjusted count of element e ∈ K
K = ∅; // Initialize while ( not end of stream ) { x = next item in stream; /* ------------------------------------- Insert phase ------------------------------------- */ if ( x ∈ K ) { count[x]++; } else { insert x into K; count[x] = 1; } /* ---------------------------------- Delete phase ---------------------------------- */ if ( |K| > 1/θ ) { for ( each e in K ) { count[e]--; if ( count[e] == 0 ) { delete e from K; } } } } Output: K contains all elements with frequency > θN
- Theorem 2.3a:
- The size of the output set K is at most equal to 1/θ elements
Proof:
- The final phase of the algorithm
is the delete phase
- The delete phase is
triggered when
|K| > 1/θ
It will delete at least one element
(Specifically, the newly inserted element that caused K to become larger than 1/θ will be deleted along with other elements whose count has become 1)
- Therefore, when the algorithm terminates, |K| is at most equal to 1/θ
- Theorem 2.3b:
- The heavy elements with count ≥ θN are included in the output K of the algorithm
Proof:
- To proof that
A &sube B, we
can show that:
- ∀ x ∈ A: x ∈ B
- In this case, it is easier to
show the reverse:
- A &sube B
⇔
∀ x ∉ B:
x ∉ A
See:
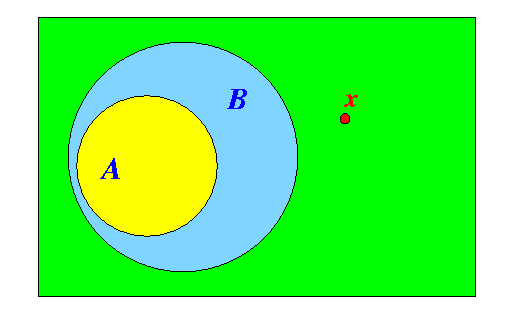
- A &sube B
⇔
∀ x ∉ B:
x ∉ A
- Let a ¬in K
be an arbitrary element that was
not included
in K
at the end of the algorithm
Let fx(a) be the (actual) number of occurence of a in the input stream
(fx(a) > 0, otherwise the proof is trivial...)
- Therefore,
a was
delete by the
delete phase
The delete phase will decrement the count of each element in the current set K when the |K| > 1/θ
- Therefore,
each occurence of
a was
deleted together with 1/θ -1
other symbols
So the total number of symbols deleted due to the removal of a is:
- fx(a)
×
(1
(a)
+ (1/θ - 1)
(the other symbols))
- Or: fx(a) × 1/θ
- fx(a)
×
(1
(a)
+ (1/θ - 1)
(the other symbols))
- There are at most N
symbols removed, therefore:
- fx(a)
×
1/θ
<
N
- Or: fx(a) < θN
- fx(a)
×
1/θ
<
N
- Since
fx(a)
<
θN,
it follows that:
- x ∉ I(x,θ)
- In other words:
- ∀ x ∉ K: x ∉ I(x,θ)
- Therefore: I(x,θ) &sube K