- Different queries
has different memory requirements
- The simplest query is
a filter:
SELECT * FROM R WHERE R.A = value
- To process the above
query, we only need to buffer
one tuple
Other queries may require an infinite amount of buffer space to compute the exact answer...
Example:
SELECT * FROM R, S WHERE R.A = S.ATo find the exact answer to the above query, all the tuples from R and S must be present and accounted for.
- This is usually not a problem in
traditional database systems
But in a stream database where data is constantly generated, we need to wait an indefinite amount of time to obtain all tuples...
So finding the exact answer to join queries is usually not the goal of a stream database system
- In the paper studied in this webpage, we aim to
answer the question:
- When is it possible to obtain exact answers to a stream database query
- Recall from
Database Systems that:
-
The project operator removes one or more attributes from
a data set.
- Example: π(FName, LName)
Phone book FName LName Phone Project FName LName ======================== -------> ============== John Smith 123-5678 John Smith Jane Smith 123-5678 Jane Smith John Doe 234-2039 John Doe Jack Rabbit 876-9876 Jack Rabbit
- In practice, for
efficiency reasons,
there are 2 flavors
of the project operation:
- Duplicate preserving projection
- this operation will not remove
duplicate tuples
- Duplicate removing projection - this operation will will remove duplicate tuples
Obviously, the duplicate removing projection requires searching and it has more overhead
- Duplicate preserving projection
- this operation will not remove
duplicate tuples
- Example
Duplicate-preserving
project operator (π+):
Phone book FName LName Phone Project LName Phone ======================== -------> ============== John Smith 123-5678 Smith 123-5678 Jane Smith 123-5678 Smith 123-5678 John Doe 234-2039 Doe 234-2039 Jack Rabbit 876-9876 Rabbit 234-2039
- Notice that from the results of the duplicate-preserving projection,
we can tell how many of original entries had the
values "Smith 123-5678".
- This fact will be important in determining the correctness of queries that use duplicate-preserving projection: if the number of duplicates outputted by an approximation algorithm is wrong, then the approximation is in error.
- Notice that from the results of the duplicate-preserving projection,
we can tell how many of original entries had the
values "Smith 123-5678".
- Example:
Duplicate-removing
project operator (π):
Phone book FName LName Phone Project LName Phone ======================== -------> ============== John Smith 123-5678 Smith 123-5678 Jane Smith 123-5678 John Doe 234-2039 Doe 234-2039 Jack Rabbit 876-9876 Rabbit 234-2039
- Notice that from the results of the duplicate-eliminating projection,
we can NOT tell how many of original entries had the
values "Smith 123-5678".
- Notice that from the results of the duplicate-eliminating projection,
we can NOT tell how many of original entries had the
values "Smith 123-5678".
- We will consider the following
model continuous query
to understand the memory requirements
of continuous queries:
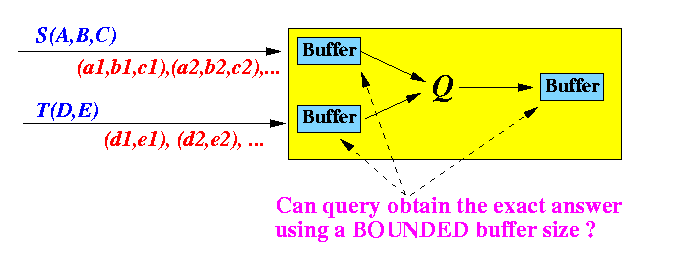
With:
- 2 input streams: S(A,B,C) and T(D,E) - 2 streams is the minimum, queries on one stream is not general enough...
- Data in input stream S has 3 attributes: A, B and C
- Data in input stream T has 2 attributes: D and E
- We will study the question:
- Can a given continuous query obtain the exact answer using a bounded amount of memory space ?
- The ultimate question that we want to answer is:
- WHEN can a continuous query obtain the exact answer using a bounded amount of memory space ?
- But first, we will study a number of sample queries to gain some insight into the problem...
- NOTE:
- the operator π in the examples can mean: duplicate-preserving OR duplicate-removing.
The outcome may be different... we need to evaluate the query for BOTH types of projection operators.
-
Example 1A: Find all A values in S with A > 10
- For duplicate-preserving π+:
-
Query can be performed in finite memory:
- σ A > 10 (S) is a filter, we do not need to store any additional information to process next incoming tuple.
- If π is duplicate-preserving, then we do not need to store any additional information to process next incoming tuple for π ( .. ) !!!
-
Query can be performed in finite memory:
- For duplicate-removing π :
-
Query can NOT
be performed in finite memory:
- If π is duplicate-removing, then
to process next incoming tuple for π ( .. ),
we need all previous tuples
in the output
to decide whether the new tuples is "new".
Storing all previous tuples in the output requires unbounded storage...
- If π is duplicate-removing, then
to process next incoming tuple for π ( .. ),
we need all previous tuples
in the output
to decide whether the new tuples is "new".
-
Query can NOT
be performed in finite memory:
π A ( σ A > 10 (S) )
- For duplicate-preserving π+:
-
Example 1B: Find all A values in S with A > 10 and
A < 20
- For duplicate-preserving π+:
-
Query can be performed in finite memory:
- σ A > 10 ∧ A < 20 (S) is a filter, we do not need to store any additional information to process next incoming tuple.
- If π is duplicate-preserving, then we do not need to store any additional information to process next incoming tuple for π ( .. ) !!!
-
Query can be performed in finite memory:
- For duplicate-removing π :
-
Query can NOT
be performed in finite memory:
- If π is duplicate-removing,
the query will
output a value
only if it has not been
outputted before
- Because there is
a finite number of different value of A
(A = 11, 12, 13, ..., 19),
we can
remember which
value of A has
already been output !
E.g.: Output[11] = true if the value "11" has already been output.
- So we can find the exact answer with finite amount of memory
- If π is duplicate-removing,
the query will
output a value
only if it has not been
outputted before
-
Query can NOT
be performed in finite memory:
π A ( σ A > 10 ∧ A < 20 (S) )
- For duplicate-preserving π+:
-
Example 2:
Join S and T on A=D
- We have discussed this above already.
It is re-stated here for completeness
- Query can NEVER be performed in finite memory without compromising
accuracy:
- To compute the join S x T,
you need to same every tuple in S and in T
- If a new tuple from S arrives, you need every T tuple to determine the result, and vice versa.
- To compute the join S x T,
you need to same every tuple in S and in T
π A ( σ A=D ( S x T ) )
- We have discussed this above already.
-
Example 3:
Another join on S and T on A=D
- Suppose A and D are integer valued
(otherwise, A=D on non-integers is kinda strange).
- Unlike the query in Example 2,
this query CAN
be processed in finite memory space without compromising
accuracy !
- How ???
- Summarize the
input tuples !
- IF the summary information is finite and can be used to answer the query exactly, we can process the query in finite memory !
Consider the following summary information:
- Keep 2 lists of values in S and T,
along with a count on the
number of values "A" and "D" between 10 and 20, in the tuples
that you have encountered so far in the input.
Pictorially:
- ACnt[i] = number of tuples s seen in the input with s.A = i
- DCnt[j] = number of tuples t seen in the input with t.D = j
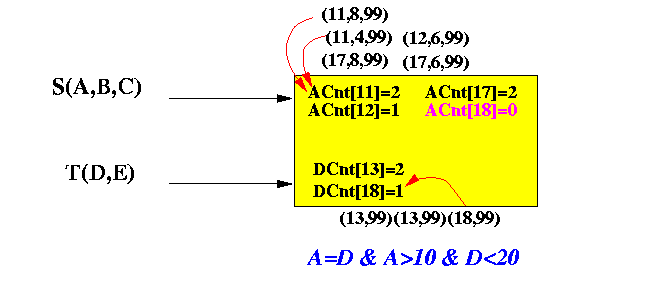
- Summarize the
input tuples !
- Finding the exact answer
for duplicate-removing π :
- Important fact:
- The duplicate-removing π will only output one value when that value occurs in some tuple s.A and some tuple t.D
- For each incoming tuple
s from S,
check if s.A is between 10 and 20.
For a tuple with s.A is between 10 and 20 do:
- If DCnt[s.A] > 0
and
ACnt[s.A] = 0
then ( the value t.A has not been
outputted yet):
- output value t.A
- ACnt[s.A]++
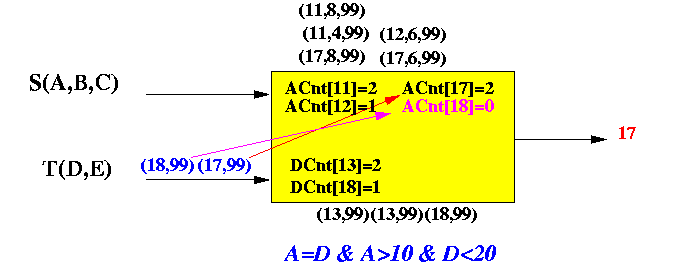
Example:
- (13, 1, 99): Finds
- ACnt[13] = 0
- DCnt[13] > 0
- Output 13
- (19, 1, 99): Finds
- ACnt[19] = 0
- DCnt[19] = 0
- Do not output 19

How an arriving S tuple is processed:
NOTE: After processing the tuples, ACnt[13] and ACnt[19] will be increased by 1 (not shown in figure)
- If DCnt[s.A] > 0
and
ACnt[s.A] = 0
then ( the value t.A has not been
outputted yet):
- For each incoming tuple
t from T,
check if t.D is between 10 and 20.
If t.D is between 10 and 20 then:
- If ACnt[t.D] > 0
and
DCnt[t.D] = 0
(then the value t.D has not been
outputted yet):
- output value t.D
- DCnt[t.D]++
Example:
The explanation is similar to the processing of an S-tuple... NOTE: DCnt[17] and DCnt[18] will be increased by 1 (not shown in figure)
- If ACnt[t.D] > 0
and
DCnt[t.D] = 0
(then the value t.D has not been
outputted yet):
- Important fact:
- Finding the exact answer
for duplicate-preserving
π+:
- Important fact:
- The duplicate-preserving π
will output
DCnt[k] values of k for each
new matching
tuple with s.A = k and
will output ACnt[k] values of k for each new matching tuple with t.D = k
- The duplicate-preserving π
will output
DCnt[k] values of k for each
new matching
tuple with s.A = k and
- For each incoming tuple
s from S,
check if s.A is between 10 and 20.
If s.A is between 10 and 20 then:
- Output DCnt[t.A]
number of values "s.A"
- ACnt[s.A]++
Example:
- (13, 1, 99): Finds
- DCnt[13] = 2
- Output 2 values
"13"
(Because the tuple (13, 1, 99) will match up with 2 tuples in T that has t.D = 13)
- DCnt[13] = 2
- (19, 1, 99): Finds
- DCnt[19] = 0
- Do not output
"19"
(Because there were no tuples t in T with t.D = 19)
- DCnt[19] = 0
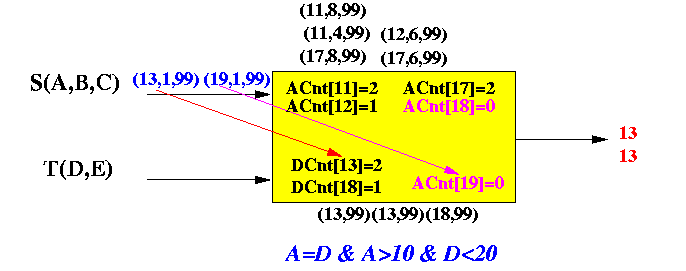
How an arriving S tuple is processed:
NOTE: ACnt[13] and ACnt[19] will be increased by 1 (not shown in figure)
- Output DCnt[t.A]
number of values "s.A"
- For each incoming tuple t from T, check if t.D is between 10 and 20.
If t.D is between 10 and 20 then:
- Output "ACnt[t.D]"
number of values of t.D
- DCnt[t.D]++
Example: (it's similar to the one above)
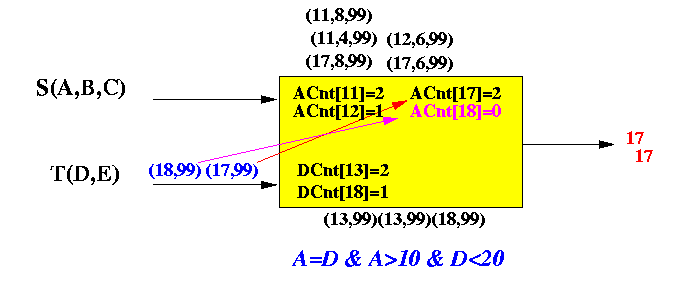
How a T tuple is processed. NOTE: DCnt[17] and DCnt[18] will be increased by 1 (not shown in figure)
- Output "ACnt[t.D]"
number of values of t.D
- Important fact:
π A ( σ A=D ∧ A > 10 ∧ D < 20 ( S x T ) )
- Suppose A and D are integer valued
(otherwise, A=D on non-integers is kinda strange).
-
Example 4:
A very subtle example....
- Range of values for
S.A is
limited
(Assuming that S.A is integer, there are 9 different values for S.A: 11, 12, .., 19)
π A ( σ B < D ∧ A > 10 ∧ A < 20 ( S x T ) ) Important characteristic of this query:
- Range of values for
S.A is
limited
- Assume that
the project operation is
duplicate-removing
(This fact is very important in this example).
- Consider this example to find out what is
important to process an
arriving T tuple.
- 3 tuples from S arrives:
(12,6,99),
(12,8,99),
(11,4,99)
- Then the tuple (7,99)
from T arrives.
What information is essential to process the condition B < D ∧ A > 10 ∧ A < 20 ?
- The tuples
(12,8,99) and
(12,6,99)
have the
same value for A = 12
(The attribute value A=12 will be outputted if the query condition is satisfied)
- The tuple
(12,8,99) can be
"discarded" if we retain
the tuple
(12,6,99)
for the purpose of
processing the above query
Reason:
- The tuple
(12,6,99) will cause
the query to
output the value "12"
whenever
6 < D.
- The tuple (12,8,99)
will also make the query
output the value "12"
but whenever
8 < D.
The range 8 < D is included in the range 6 < D
So the tuple (12,8,99) is not necessary when we retain the tuple (12,6,99)
- The tuple
(12,6,99) will cause
the query to
output the value "12"
whenever
6 < D.
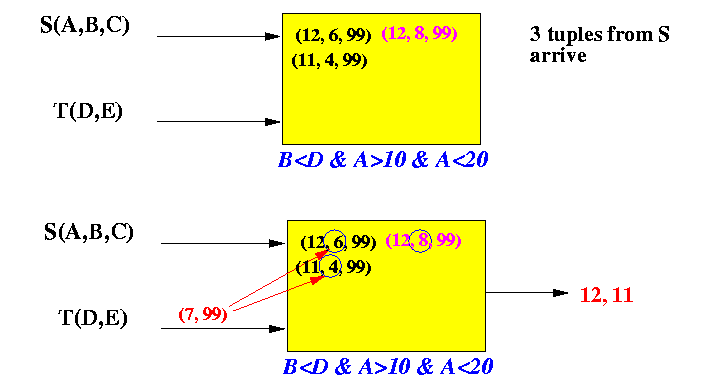
- The tuples
(12,8,99) and
(12,6,99)
have the
same value for A = 12
Important:
- A similar argument holds for
all tuples
with other attribute A values:
- Keep the
smallest B-attribute value
that is associated with the
attribute A = 11
- Keep the
smallest B-attribute value
that is associated with the
attribute A = 12
- And so on... for:
-
attribute A = 11,
attribute A = 12, ...
attribute A = 19
- Keep the
smallest B-attribute value
that is associated with the
attribute A = 11
- 3 tuples from S arrives:
(12,6,99),
(12,8,99),
(11,4,99)
- Now consider this example to find out what is
important to process an
arriving S tuple.
- 3 tuples from T arrives:
(10,4),
(16,4),
(20,4)
- Then the tuple (12,18,99)
from S arrives.
What information is essential to process arriving S tuple ?
- The tuples
(10,7) and
(16,1)
can both be
"discarded" if we retain
the tuple
(20,4)
for the purpose of processing
B < D
Reason:
- If we retain (20,4),
the query will output
s.A whenever
s.B < 20
- The tuple (10,7)
will make the query
output the value "s.A"
whenever
s.B < 10.
The tuple (16,1) will make the query output the value "s.A" whenever s.B < 16.
The ranges s.B < 10 and s.B < 16 are included in the range s.B < 20
So we only need to remember the largest value in the D attributes
- If we retain (20,4),
the query will output
s.A whenever
s.B < 20
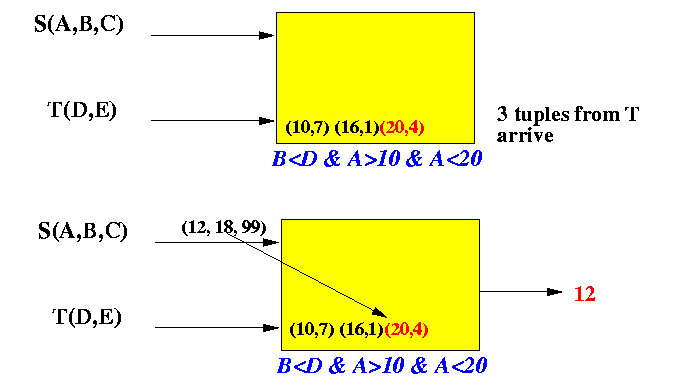
- The tuples
(10,7) and
(16,1)
can both be
"discarded" if we retain
the tuple
(20,4)
for the purpose of processing
B < D
- 3 tuples from T arrives:
(10,4),
(16,4),
(20,4)
-
Information needed to process
s.B < t.D ∧ s.A > 10 ∧ s.A < 20
using
duplicate-removing π :
- We maintain 9 different
minimum values BMIN[i],
i = 11, 12, ..., 19
- BMIN[11] =
the minimum value of attribute B
for a corresponding attribute value
s.A = 11
- BMIN[12] =
the minimum value of attribute B
for a corresponding attribute value
s.A = 12
- ...
- BMIN[19] = the minimum value of attribute B for a corresponding attribute value s.A = 19
These information are used to process an incoming T tuple t:
- If BMIN[k] < t.D, k = 11, 12, .., 19, (and k has not been output yet - use an extra flag bit to signal this), then output "k"
- BMIN[11] =
the minimum value of attribute B
for a corresponding attribute value
s.A = 11
- And we maintain the
maximum value
( DMAX)
which is the
maximum values of the D attribute
seen so far.
- DMAX = maximum values of the D attribute in the tuples in stream T
This information are used to process an incoming S tuple s:
- If s.B < DMAX, (and s.A has not been output yet - use an extra flag bit to signal this), then output "s.A"
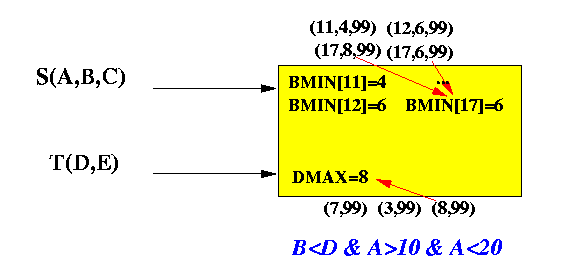
Example of information content:
-
After processing:
- 4 tuples from S
(11,4,99), (12,6,99), (17,8,99), (17,6,99),
and
- 3 tuples from T (7,99), (3,99), (8,99)
- BMIN[11] = 4 due to tuple (11,4,99)
- BMIN[12] = 4 due to tuple (12,6,99)
- BMIN[17] = 6 due to tuple
(17,6,99)
- DMAX = 8 due to tupe (8,99)
- Uses s.B = 4 to compare against
DMAX = 8
Because s.B < 8, we may output s.A = 12 - depending on whether the value "12" has been output before (remember that π used is duplicate-removing)
(We can use a output[11..19] array to indicate if a value has been output already)
- Uses s.A = 12 to index into
BMIN[12] = 6
Because 4 < 6, updates BMIN[12] = 4
- Test BMIN[11] (4) < 5, results
in true, so we output
11
(if this value has not been outputted yet)
- Test BMIN[12] (6) < 5, results
in false, do NOToutput
12
- and so on...
- Finally, we update DMAX (which is not changed because 5 < 8)
the data structure will contain:
Processing an incoming S tuple:
if ( s.A > 10 && s.A < 20 ) { if ( s.B < DMAX ) if s.A has not been outputted then Output s.A set output[s.A] = true; if ( s.B < BMIN[s.A] ) BMIN[s.A] = s.B; }Graphically:
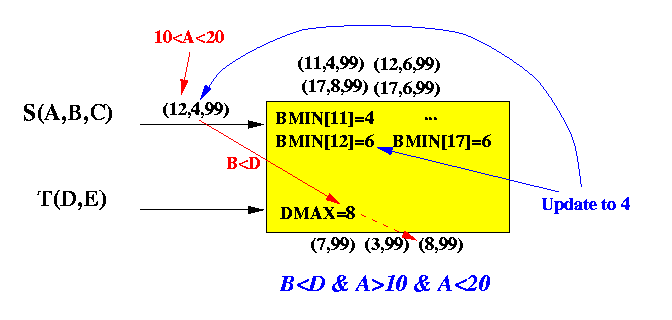
When (12,4,99) arrives:
Processing an incoming T tuple
for i = 11, 12, ..., 19 do if ( BMIN[i] < t.D ) if i has not been outputted then Output i set output[i] = true; if ( t.D > DMAX ) DMAX = t.D;Graphically:
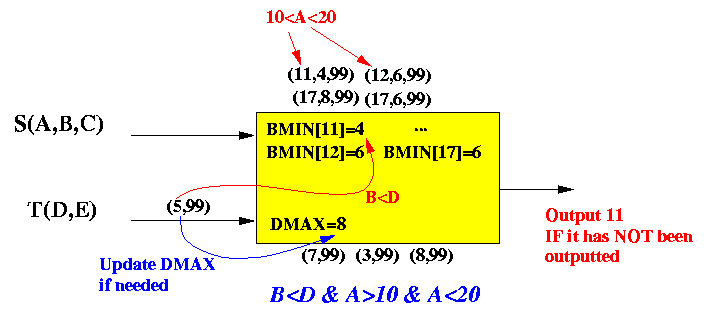
When t(5,99) arrives:
- We maintain 9 different
minimum values BMIN[i],
i = 11, 12, ..., 19
- Very interesting fact about this example:
- The answer of this query can be computed
exactly for
duplicate-removing π
- But cannot be done for duplicate-pre-serving π
So it is the opposite to a simple project query !
- The answer of this query can be computed
exactly for
duplicate-removing π
- Why
the query:
π A ( σ B < D ∧ A > 10 ∧ A < 20 ( S x T ) ) cannot be processed with exact accuracy with limited amount of memory.
Example:
- Suppose the typle t(47,99)
arrives.
- In order to
output the correct number
of values for say s.A = 12,
we need to know the
exact number of tuples
(12,x,..)
where x < 47
- We must do this not only for the value "47", but also every integer value
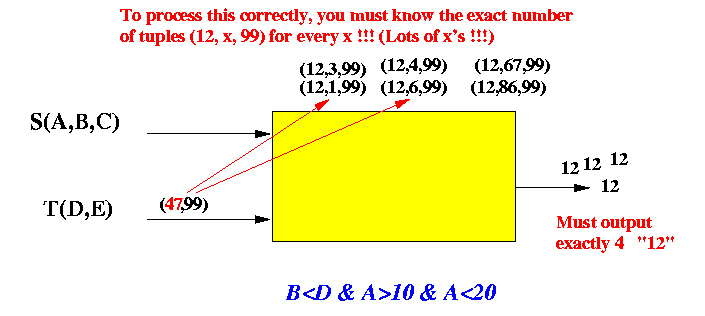
Since there is an infinite number of integers, this is not feasible.
- Suppose the typle t(47,99)
arrives.
- This is the $6,000,000 question presented and studied in the paper....
- I will only summarize the results in the paper... (no proofs)
- SPJ = Select-Project-Join (query)
- Q = Query (continuous query)
- S(Q) = the set of Streams that
appear in Q
- C(Q) = the set of Constants (values) that
appear in Q
- A(Q) = the set of Attributes in all streams that
appear in Q
- E(Q) = the set of Elements that appear in Q
-
E(Q) = A(Q) ∪ C(Q)
- A(s) = the set of Attributes in stream s
- E(s) = A(s) ∪ C(Q)
- P = the set of Atomic Predicates
(atomic boolean expressions)
-
Atomic predicates do not have
∧ and ∨ operators
E.g.: P = {A < B, B < C}
- P+ = closure of P
-
set of (atomic) predicates that are
logically implied by the predicates in P
E.g.: P+ = {A < B, B < C, A < C}
- IND(P,E) = the set of predicates in P+ that only involve elements in E
|
|
- A filter selects
tuples in a stream that satisfies a
condition
- Filter:
- A filter
is an atomic predicate
whose operands
are either:
- an attribute
and a constant:
-
i.e, of the form:
si.A COMPARE k
- two attributes
of the same stream:
-
i.e., of the form:
si.A COMPARE si.B
(in this case, we compare 2 values in the same tuple)
- an attribute
and a constant:
- A filter
is an atomic predicate
whose operands
are either:
- Filters can be combined
to make composite predicates
- AND construct using Filters
Filter1 AND Filter2: +---------+ +---------+ S -----> | Filter1 | -------> | Filter2 | -------> output +---------+ +---------+ - OR construct using Filters
Filter1 OR Filter2: +---------+ +--> | Filter1 | ---+ | +---------+ | | | --->+ + -----> output | | | +---------+ | +--> | Filter2 | ---+ +---------+
- Filters is an important class of atomic predicate because they form the basis to study when a stream query can obtain the exact solution with finite memory buffer
- One of the more trivial property that determines whether a query
can be processed without losing accuracy is:
- the boundedness
of the attributes.
- An attribute is bounded is the number of values that it can take on is finite (bounded)...
- the boundedness
of the attributes.
- An attribute is a characteristic of an entity,
for example: age, color, salary.
Each attribute has a value: age=60, color="red", salary=40,000, etc.
- Attributes can be part of predicates (a predicate is a
boolean condition, like "A < 10").
- Lower bounded attribute:
- An attribute A is
lower bounded
by a given set of predicates P if
there exists an atomic predicate
-
"k < A" ∈ P+
for some constant k
- An attribute A is
lower bounded
by a given set of predicates P if
there exists an atomic predicate
- Upper bounded attribute:
- An attribute A is
upper bounded
by a given set of predicates P if
there exists an atomic predicate
-
"A < k" ∈ P+
for some constant k
- An attribute A is
upper bounded
by a given set of predicates P if
there exists an atomic predicate
- And finally, bounded attribute:
- An attribute A is
bounded
by a given set of predicates P if
there exists an atomic predicate
-
"k1 < A < k2"
∈ P+
for some constants k1 and k2
- An attribute A is
bounded
by a given set of predicates P if
there exists an atomic predicate
- Property:
- If an attribute A is
bounded, then
the
number of different values
that attribute A
can take on is
finite
This ofcourse will affect how much information you need to store when you need to process a query without any loss of accuracy that test on values of A !
- If an attribute A is
bounded, then
the
number of different values
that attribute A
can take on is
finite
- Clearly:
- An unbounded attribute
is one that is not bounded
Such an attribute can be lower bounded or upper bounded or neither.
- Exactly solutions to a query cannot be obtained for queries that contain unbounded attributes
- An unbounded attribute
is one that is not bounded
- Totally Ordered set:
- Let E
be a set of elements
(i.e., attributes and constants)
- Let P be a set of predicates (atomic boolean expressions)
-
∀ e1 and e2 ∈ E:
exactly one
of these predicates is found in
P+:
- e1 < e2
- e1 > e2
- e1 == e2
E is totally ordered by P if:
- Let E
be a set of elements
(i.e., attributes and constants)
- Example:
- Let E = {A, B, 5} (a set of attributes and constants)
- Let P = {A < B, 5 < A}
- Then:
- P+ = {A < B, 5 < A, 5 < B}
(Because 5 < B follows from A < B ∧ 5 < A)
- P+ = {A < B, 5 < A, 5 < B}
- Claim:
- E is totally ordered by P
- Proof:
- We verify for every pair of elements e1 and e2
(there are 3 possible pairs, namely
(A,B), (A,5) and (B,5)),
that exactly one of e1 < e2,
e1 > e2 and e1 == e2
appears in P+:
- The pair (A,B): only constraint "A < B" ∈ P+
- The pair (A,5): only constraint "5 < A" ∈ P+
- The pair (B,5): only constraint "5 < B" ∈ P+
- We verify for every pair of elements e1 and e2
(there are 3 possible pairs, namely
(A,B), (A,5) and (B,5)),
that exactly one of e1 < e2,
e1 > e2 and e1 == e2
appears in P+:
- The elements in a Totally Ordered set can be ranked in a unique manner
- Example:
- P+ = {A < B, 5 < A, 5 < B}
- Ranking of the elements:
-
5 < A < B
- P+ = {A < B, 5 < A, 5 < B}
|
|
- The theory on
when a stream query
can obtain
the exact solution
using bounded memory
is based on the concept of
"Locally Totally Ordered queries"
(which are based on
the two properties above).
- Locally Totally Ordered query:
- A query Q(P)
using the predicate P
is a
Locally Totally Ordered query
if
- for every stream s in query Q(P), the elements in stream s (= E(s)) are totally ordered by the predicate P
- A query Q(P)
using the predicate P
is a
Locally Totally Ordered query
if
- In order words:
- The predicate P of Locally Totally Ordered query imposes a total ordering on the elements in each stream.
- Example: S(A,B)
-
π A (
σ A < B ∧ 5 < A
(S) )
Remember just a moment ago, we showed that the predicate P = {A < B, 5 < A} has a closure:
-
P+ =
{A < B, 5 < A,, 5 < B}
- The Locally Totally Ordered query is very important
step towards
answering the question:
-
When can a stream query
obtain the exact solution
using finite amount of buffer
And P+ imposes a total ordering on {5, A, B}.
Hence, the above query is a Locally Totally Ordered query.
- The Locally Totally Ordered query is very important
step towards
answering the question:
- In order to determine if a stream query
can obtain the exact solution
using finite amout of buffer space,
we must:
- Decompose a stream query
into a union of
Locally Totally Ordered queries
- Check for some properties for each Locally Totally Ordered queries
- Decompose a stream query
into a union of
Locally Totally Ordered queries
- A very important question to this end is:
- Can we always decompose a stream query into a union of Locally Totally Ordered queries ???
- Theorem 4.1 of the paper states that it can always be done...
- I will not present the proof of the following theorem (Theorem 4.1
in the paper) because we are only interested in the results.
Theorem 4.1 -
Any query
can be broken up
into a
union
of Locally Totally Ordered queries
- Consider the query of the streams S(A,B,C) and T(D,E):
π A ( σ A=D ∧ A > 10 ∧ D < 20 ( S x T ) )
- Summary of the relevant information:
- The streams in the query are:
- S and T
- The attributes in the streams are:
- S: A, B, C
- T: D, E
- The constant (elements)
in the query are:
- 10, 20
- The streams in the query are:
- First consider the predicate
" A=D ∧ A > 10 ∧ D < 20 "
applied only on
on
stream S(A, B, C):
- Is
{A, B, C, (10, 20)}
totally ordered by
P = " A=D ∧ A > 10 ∧ D < 20 "
- Answer: NO because:
- B compareTo C is not a predicate in P+
In fact:
-
The only ordering that we can impose on the
elements of S and the constants is:
- 10 < A
We can't order the other elements...
So there is a stream (namely S(A,B,C)) where we can't impose an ordering.
And therefore:
-
π A ( σ
A=D ∧ A > 10 ∧ D < 20
( S x T ) )
is not a Locally Totally Ordered query
- Is
{A, B, C, (10, 20)}
totally ordered by
P = " A=D ∧ A > 10 ∧ D < 20 "
- Theorem 4.1
says that we can
decompose
this
query as a
union
of a number of
Locally Totally Ordered queries.
Here is how it can be done:
A=D ∧ A > 10 ∧ D < 20 = (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 < E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 = E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 > E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C = B ∧ 20 < E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C = B ∧ 20 = E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C = B ∧ 20 > E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C > B ∧ 20 < E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C > B ∧ 20 = E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C > B ∧ 20 > E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B = 10 ∧ C < B ∧ 20 < E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B = 10 ∧ C < B ∧ 20 = E) ∨ (A=D ∧ A > 10 ∧ D < 20 ∧ B = 10 ∧ C < B ∧ 20 > E) ... and so on (complete the serie)
- Now consider the following predicate:
- A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 < E
- Consider the elements in
S: {A,B,C}
and the constants (10 and 20).
The predicate "A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 < E" imposes the following ordering on the elements {A, B, C, 10, 20}:
- C < B < 10 < A < 20
- Now, consider the
elements
in
stream T: {D,E}
and the
constants (10, and 20)
The predicate "A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 < E" imposes the following ordering on the elements {D, E, 10, 20}:
- 10 < D < 20 < E
Therefore, the query
-
π A ( σ
A=D ∧ A > 10 ∧ D < 20
∧ B < 10 ∧ C < B ∧ 20 < E
( S x T ) )
is a Locally Totally Ordered query.
- Consider the second predicate
derived from
the original query:
- A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 = E
- Consider the elements in
S: {A,B,C}
and the constants (10 and 20).
The predicate "A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 = E" imposes the following ordering on the elements {A, B, C, 10}:
- C < B < 10 < A
(The constant 20 is not involved in any relation with an attribute in stream S - so we do not need to include it)
- Now, consider the
elements
in
stream T: {D,E}
and the
constants (10, and 20)
The predicate "A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 = E" imposes the following ordering on the elements {D, E, 10, 20}:
- 10 < D < 20 = E
Therefore, the query
-
π A ( σ
A=D ∧ A > 10 ∧ D < 20
∧ B < 10 ∧ C < B ∧
20 = E
( S x T ) )
is also a Locally Totally Ordered query.
- You can see that each of the derived queries
will be more strict than the orginal
query (due to additional ∧ clauses that must be satisfied).
In other words, each derived Locally Totally Ordered query will retrieve a portion of the tuples that the original query.
- Thus, we can union the results from all the derived
Totally Ordered queries and obtain the tuples
output by the original (general) query:
π A ( σ A=D ∧ A > 10 ∧ D < 20 ( S x T ) ) = π A ( σ A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 < E ( S × T ) ) ∪
π A ( σ A=D ∧ A > 10 ∧ D < 20 ∧ B < 10 ∧ C < B ∧ 20 = E ( S × T ) ) ∪
... (and so on, a lot more Totally Ordered queries)
That's the gist of Theorem 4.1...
- Remember that we are trying to find out:
- when a stream query can be executed without loss of accuracy using finite amount of memory
- Theorem 4.1
tells us that:
- a stream query can always be broken up into a union of (special) Locally Totally Ordered queries
- Fact:
- If every Locally Totally Ordered query of the union can obtain the exact answer using finite amount memory, then then original stream query can also do that !
- In other words:
- we have simplified
the original problem to
one where we know a lot
about the predicate
(A Locally Totally Ordered query imposes a total ordering in the elements in every stream)
- we have simplified
the original problem to
one where we know a lot
about the predicate
- What must happen next is to find properties on when a Locally Totally Ordered query can be executed without loss of accuracy using finite amount of memory !!!
- We need 2 more definitions
before we can state the final theorem
that tells us
when a stream query
can obtain the exact answer
with finite memory
- MaxRef(s):
- MaxRef(s)
= the set of all
unbounded attribute
A in stream s
that participate in an
inequality join with
another stream o
of the form
o.B < s.A
I.e., the unbounded attribute s.A of stream s is used as an upperbound for an attribute in another stream.
- Recall that unbounded means not bounded - the attribute can be upper bounded, or lower bounded, or neither .
Example: streams S(A,B,C) and T(D,E)
- σ A < D (S x T)
- Attribute D of stream T is unbounded and it is used as an "upperbound" for attribute A of another stream
- MaxRef(s)
= the set of all
unbounded attribute
A in stream s
that participate in an
inequality join with
another stream o
of the form
o.B < s.A
- MaxRef(s):
- MinRef(s)
= the set of all
unbounded attribute
A in stream s
that participate in an
inequality join with
another stream o
of the form
s.A < o.B
I.e., the unbounded attribute s.A of stream s is used as an lowerbound for an attribute in another stream.
- MinRef(s)
= the set of all
unbounded attribute
A in stream s
that participate in an
inequality join with
another stream o
of the form
s.A < o.B
- We have now learned about
all the necessary information
to formulate the
theorem about processing stream queries with bounded memory space.
- There are 2 different theorems:
- one for the case when the project operation is duplicate-preserving and
- one when the project operation is duplicate-removing....
Duplicate-preserving projection queries
- Theorem 4.2 of the paper states
when a
stream query can obtain the
exact answer
using
finite amount of memory
when projection is
duplicate-preserving
- Theorem 4.2:
- Let
Q(P):
- Q(P) = π project-attr-list ( σP ( S1 x S2 x .. x Sn ) )
be a Locally Totally Ordered stream query using input streams S1, S2, .. Sn.
(Remember, due to Theorem 4.1 above, we can reduce a general stream query to a set of Locally Totally Ordered queries)
The predicate for query Q(P) is P.
Q(P) uses duplicate-preserving projection.
- Theorem 4.2:
The stream query Q(P) can obtain the exact answer without loss of accuracy using a bounded amount of memory ("bounded memory computatble") if and only if all these 3 conditions hold:
- Every attribute in the
project attribute list is
bounded
- In every
equal-join predicate
between 2 different streams:
- Si.A = Sj.B i ≠ j
both attributes Si.A and Sj.B must be bounded.
- For every stream s:
- |MaxRef(s)| = 0, and
- |MinRef(s)| = 0
In other words:
-
There are
no
unbounded attributes
in any streams
used in
unequality join
operation with
any other stream.
- Every attribute in the
project attribute list is
bounded
- Let
Q(P):
- Input streams S(A,B,C) and T(D,E):

The attributes in the streams S and T are:
- A(S) = {A, B, C}, and
- A(T) = {D ,E}
- Consider the stream query:
π A ( σ A=D ∧ A > 10 ∧ D < 20 &and B > 20 &and C < 10 &and E < 10 ( S x T ) ) - Can this stream query obtain the exact answer using finite amount of memory ?
- Preliminaries: find the ordering
imposed by the
Locally Totally Ordered predicate:
- Stream S: C < 10 < A (=D) < 20 < B
- Stream T: E < 10 < D (=A) < 20
You can now see which attributes are bounded and unbounded:
- Bounded: 10 < A < 20
- Bounded: 10 < D < 20
- Unbounded: B, C, E
- Answer: check the 3 conditions
in Theorem 4.2:
- Every attribute in the
project list is
bounded
- The attributes in the project list is:
A
- A is
bounded, because:
-
10 < A < 20
So, yes:
-
Every attribute in the project list
is bounded.
- The attributes in the project list is:
A
- In every equal-join predicate between 2 different streams
-
Si.A = Sj.B (i ≠ j)
both attributes Si.A and Sj.B must be bounded.
- The equal-join predicate in:
-
A=D ∧ A > 10 ∧ D < 20 &and B > 20
&and C < 10
&and E < 10
is:
-
A=D
- A and
D are
bounded
So this condition is satisfied.
- The equal-join predicate in:
- For every stream s:
- No unbounded attributes in s involved in unequality join operation with another (different) stream.
- There are
no unequality join operations
in:
-
A=D ∧ A > 10 ∧ D < 20 &and B > 20
&and C < 10
&and E < 10
So this condition is satisfied
Conclusion:
- This stream query can obtain the exact answer using finite amount of memory.
- Every attribute in the
project list is
bounded
- How can the query does it ?
-
Use the summarization technique
(with finite number of
count registers)
that is similar to
Example 3:
click here
- Input streams S(A,B,C) and T(D,E):

The attributes in the streams S and T are:
- A(S) = {A, B, C}, and
- A(T) = {D ,E}
- Consider the stream query:
π+A ( σ B < D &and A > 10 &and A < 20 &and B > 20 &and C < 10 &and D > 20 &and E < 10 (S × T) ) Question:
- Can this stream query obtain the exact answer using finite amount of memory ?
- Preliminaries: find the ordering
imposed by the
Locally Totally Ordered predicate:
- Stream S: C < 10 < A < 20 < B
- Stream T: E < 10 < 20 < (B) < D
You can now see which attributes are bounded and unbounded:
- Bounded: 10 < A < 20
- Unbounded: B, C, D, E
- Answer: check the 3 conditions
in Theorem 4.2:
- Every attribute in the
project list is
bounded
- The attributes in the project list is:
A
- A is
bounded, because:
-
B < D &and A > 10 &and
A < 20 &and B > 20 &and C < 10
&and D > 20 &and E < 10
Because A > 10 &and A < 20 , the attribute A is bounded
So, yes:
-
Every attribute in the project list
is bounded.
- The attributes in the project list is:
A
- In every equal-join predicate between 2 different streams
-
Si.A = Sj.B (i ≠ j
both attributes Si.A and Sj.B must be bounded.
- There are no equal-join predicates...
- ... so this condition is satisfied.
- There are no equal-join predicates...
- For every stream s:
- No unbounded attributes in s involved in unequality join operation with another (different) stream.
- The unequality join operations
in:
-
B < D &and A > 10 &and A < 20 &and B > 20 &and C < 10
&and D > 20 &and E < 10
are (is):
- S.B < T.D
- The attribute S.B is unbounded...
So this condition is violated
Conclusion:
- This stream query cannot obtain the exact answer using finite amount of memory.
- Every attribute in the
project list is
bounded
- The authors gave a
very elabrate
and interesting
counter example on
why
this stream query
cannot be processed using finite memory.
Example tuple arrival:
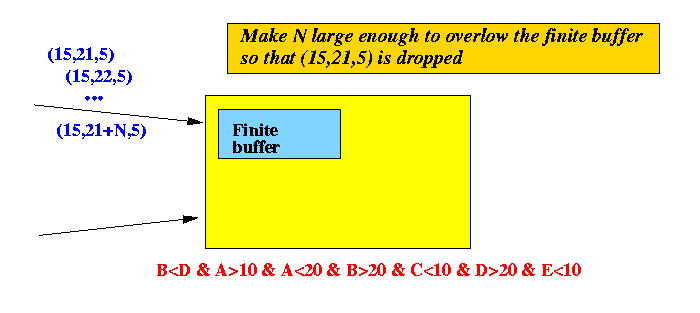
- The large number of
tuples of stream S arrives as follows:
-
(15, 21, 5),
(15, 22, 5),
(15, 23, 5),
...
(15, 21+N, 5),
- The (finite) buffer overflowed and
the tuple
(15,21,5) is
dropped...
- After dropping (15,21,5),
the T tuple
(22,5)
arrives
Situation:
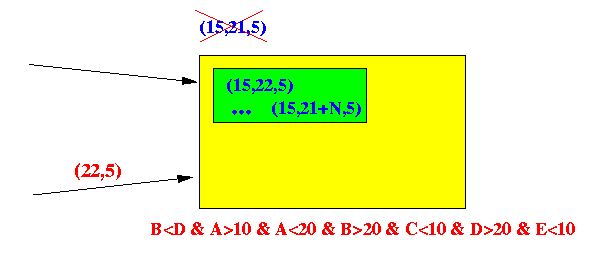
Analysis:
- The S tuple
(15,21,5)
is the
only tuple
with
S.B (21) < T.D (22)
-
Without (15,21,5),
the T tuple
(22,5)
will fail on the
condition:
S.B (21) < T.D (22)
- So the stream query will fail to find the exact answer (if finite amount of memory is used)
- The large number of
tuples of stream S arrives as follows:
Duplicate-removing projection queries
- Theorem 5.2 of the paper states
when a
stream query can obtain the
exact answer
using
finite amount of memory
when projection is
duplicate-removing
- Theorem 5.2:
- Let
Q(P):
- Q(P) = π project-attr-list ( σP ( S1 x S2 x .. x Sn ) )
be a Locally Totally Ordered stream query using input streams S1, S2, .. Sn.
(Remember, due to Theorem 4.1 above, we can reduce a general stream query to a set of Locally Totally Ordered queries)
The predicate for query Q(P) is P.
Q(P) uses duplicate-removing projection.
- Theorem 5.2:
The stream query Q(P) can obtain the exact answer without loss of accuracy using a bounded amount of memory ("bounded memory computatble") if and only if all these 3 conditions hold:
- Every attribute in the
project attribute list is
bounded
- In every
equal-join predicate
between 2 different streams:
- Si.A = Sj.B i ≠ j
both attributes Si.A and Sj.B must be bounded.
- For every stream s:
- |MaxRef(s)| + |MinRef(s)| <= 1
In other words:
-
There are
at most one
unbounded attributes
in any streams
used in
unequality join
operation with
another stream.
- Every attribute in the
project attribute list is
bounded
- Let
Q(P):
- Input streams of the query S(A,B,C) and T(D,E):

- The attributes in the streams S and
T are:
- A(S) = {A, B, C}, and
- A(T) = {D ,E}
- Consider the stream query:
πA ( σ B < D &and A > 10 &and A < 20 &and B > 20 &and C < 10 &and D > 20 &and E < 10 (S × T) )
- Preliminaries: find the ordering
imposed by the
Locally Totally Ordered predicate:
- Stream S: C < 10 < A < 20 < B
- Stream T: E < 10 < 20 < (B) < D
You can now see which attributes are bounded and unbounded:
- Bounded: 10 < A < 20
- Unbounded: B, C, D, E
- Answer: check the 3 conditions
in Theorem 5.2:
- Every attribute in the
project list is
bounded
- The attributes in the project list is:
A
- A is
bounded, because:
-
B < D &and A > 10 &and
A < 20 &and B > 20 &and C < 10
&and D > 20 &and E < 10
Because A > 10 &and A < 20 , the attribute A is bounded
So, yes:
-
Every attribute in the project list
is bounded.
- The attributes in the project list is:
A
- In every equal-join predicate between 2 different streams
-
Si.A = Sj.B (i ≠ j)
both attributes Si.A and Sj.B must be bounded.
- There are no equal-join predicates...
- ... so this condition is satisfied.
- There are no equal-join predicates...
- For every stream s:
- At most 1 unbounded attributes in s involved in unequality join operation with another (different) stream.
- The unequality join operations
in:
-
B < D &and A > 10 &and A < 20 &and B > 20 &and C < 10
&and D > 20 &and E < 10
are (is):
- S.B < T.D
- Stream S has one unbounded attribute S.B in a unequality join.
- Stream T has one unbounded attribute T.D in a unequality join.
So this condition is satisfied !!!
Conclusion:
- This stream query CAN obtain the exact answer using finite amount of memory.
- Every attribute in the
project list is
bounded
- Consider:
- π A ( σ B < D &and A > 10 &and A < 20 &and B > 20 &and C < 10 &and D > 20 &and E < 10 ( S x T ) )
Question:
- How can be obtain the exact answer with finite amount of memory ?
Answer (in the paper:)
- For queries with duplicate-eliminating
projection, it suffices to know
only whether the
bucket is empty or
whether there has been
at least one
tuple assigned to the bucket.
-
There
is, however,
one additional piece of information
that we must store for
each bucket (value of A)
in
stream Si's synopsis
when
MinRef (Si)
or MaxRef (Si) is nonempty:
- If MinRef (Si) is nonempty,
we store the the
minimum
value for any attribute in
MinRef (Si) among tuples
that have been assigned to that bucket.
In the query π A ( σ B < D &and A > 10 &and A < 20 &and B > 20 &and C < 10 &and D > 20 &and E < 10 ( S x T ) ) , we store:
- Attribute A
forms the buckets: 11, 12, 13, ..., 19
Attribute S.B is a lower bound in an inequality join
- BMin[11] = min. value in S.B in S tuples (11, B, ...)
- BMin[12] = min. value in S.B in S tuples (12, B, ...)
- BMin[13] = min. value in S.B in S tuples (13, B, ...)
- ...
- BMin[19] = min. value in S.B in S tuples (19, B, ...)
- Attribute A
forms the buckets: 11, 12, 13, ..., 19
- Similarly, if
MaxRef (Si)
is nonempty,
we store the
maximum value
for any
attribute in
MaxRef (Si)
among tuples that
have been assigned to that bucket.
In the query π A ( σ B < D &and A > 10 &and A < 20 &and B > 20 &and C < 10 &and D > 20 &and E < 10 ( S x T ) ) , we store:
- Attribute S.A
forms the buckets: 11, 12, 13, ..., 19
Attribute T.D is an upper bound in an inequality join
S.A and T.D are in different streams - you need only store the max. value
- DMax = max. value in T.D in T tuples (D, ...)
- Attribute S.A
forms the buckets: 11, 12, 13, ..., 19
- If MinRef (Si) is nonempty,
we store the the
minimum
value for any attribute in
MinRef (Si) among tuples
that have been assigned to that bucket.
- Note:
- This result should
not be a surprise !
We have seen something like this before ...
- We saw above
( click here )
that the following stream query:
- π A ( σ B < D ∧ A > 10 ∧ A < 20 ( S x T ) )
can obtain the exact answer with finite amount of memory
- The query:
- πA ( σ B < D &and A > 10 &and A < 20 &and B > 20 &and C < 10 &and D > 20 &and E < 10 (S × T) )
is one of the sub-queries of π A ( σ B < D ∧ A > 10 ∧ A < 20 ( S x T ) )
- Since the original query
π A ( σ
B < D ∧ A > 10 ∧ A < 20
( S x T ) )
can obtain the exact answer
with finite amount of memory,
then
all its
derived Locally Totally Ordered queries
must also be able to
obtain the exact answer
with finite amount of memory !!!
(because if we lose some accuracy in any of the sub-queries, we will not be able to use the union to compile an accurate final result....)
- This result should
not be a surprise !
- Consider the stream query:
πA ( σ B < D &and C < E ∧ A > 10 &and A < 20 &and B > 20 &and C < 10 &and D > 20 &and E < 10 (S × T) ) (This query differs from the previous one by only the extra clause C < E )
- Preliminaries: find the ordering
imposed by the
Locally Totally Ordered predicate:
- Stream S: C < 10 < A < 20 < B
- Stream T: E < 10 < 20 < (B) < D
You can now see which attributes are bounded and unbounded:
- Bounded: 10 < A < 20
- Unbounded: B, C, D, E
- Answer: check the 3 conditions
in Theorem 5.2:
- Every attribute in the
project list is
bounded
- The attributes in the project list is:
A
- A is
bounded, because:
-
B < D &and
C < E
∧ A > 10 &and
A < 20 &and B > 20 &and C < 10
&and D > 20 &and E < 10
Because A > 10 &and A < 20 , the attribute A is bounded
So, yes:
-
Every attribute in the project list
is bounded.
- The attributes in the project list is:
A
- In every equal-join predicate between 2 different streams
-
Si.A = Sj.B (i ≠ j)
both attributes Si.A and Sj.B must be bounded.
- There are no equal-join predicates...
- ... so this condition is satisfied.
- There are no equal-join predicates...
- For every stream s:
- At most 1 unbounded attributes in s involved in unequality join operation with another (different) stream.
- The unequality join operations
in:
-
B < D &and
C < E
&and A > 10 &and A < 20 &and B > 20 &and C < 10
&and D > 20 &and E < 10
are:
- S.B < T.D
- S.C < T.E
- Stream S has two unbounded attributes S.B and S.C in unequality joins.
- Stream T (also) has two unbounded attributes T.D and S.E in unequality joins.
So this condition is violated !!!
Conclusion:
- This stream query cannot obtain the exact answer using finite amount of memory.
- Every attribute in the
project list is
bounded
-
The authors again
gave a very elabrate
and interesting counter example on
why
this query cannot be processed using finite memory.
- Example arrival sequence:
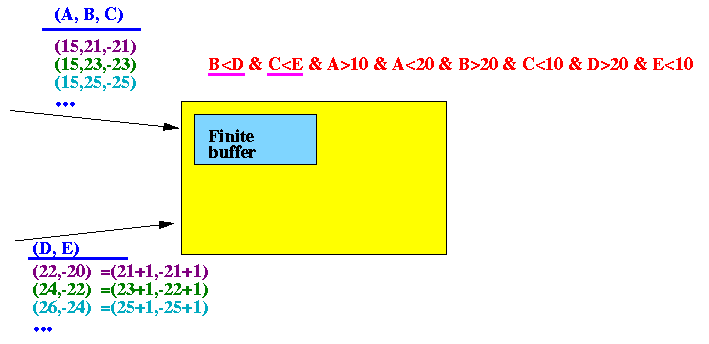
- The arrivals of the tuples are as follows:
- Stream S: (15,21,-21), (15,23,-23), (15,25,-25), ...
- Stream T: (22,-20) (= 21+1,-21+1), (24,-22) (= 23+1,-23+1), (26,-24) (= 25+1,-25+1),
- This exampleis very peculiar:
- Only
the tuples
(15,21,-21)
and
(22,-20) (= 21+1,-21+1),
join with each other
- So also,
only
the tuples
(15,23,-23)
and
(24,-22) (= 23+1,-23+1),
join with each other
- And,
only
the tuples
(15,25,-25)
and
(26,-24) (= 25+1,-25+1),
join with each other
- And so on.
- All of the above case will cause the query to output the value 15
Fact:
- we cannot predict
which T tuples will
arrive...
Therefore:
- In order to output 15 for the query, we must remember all S tuples
This requires an infinite amount of memory...
- Only
the tuples
(15,21,-21)
and
(22,-20) (= 21+1,-21+1),
join with each other