Representing signed integer numbers inside a computer

Sign-Magnity Representation Method

A straight forward encoding for signed numbers is the sign-magnitude encoding method:

First bit of the data represents the sign of the integer number
The remaining bits of the data represents the magnitude of the integer number

Example: 8 bits representaion

0 0 0 0 0 1 1 1 ^ | sign Remaining bits is the magnitude (absolute value) bit Examples: 00000111 represents 7 10000111 represents -7

Problems with the Sign-Magnity Representation Method
- There are two different representations for ZERO
  - 0000....0000 (+0) and
  - 1000....0000 (-0)
- The encoding method makes integer arithmetic very difficult:
  - 7 + 3 performs an add operation
  - 7 + (-3) performs an subtract operation
The two's complement encoding method
- Modern Computers use the two's complement encoding method to represent signed integer numbers.
- To illustrate the 2's complement encoding method, I will use a 3 bit representation
- The following figure shows how the binary number changes when you add the value 1 to a 3 bit binary number:
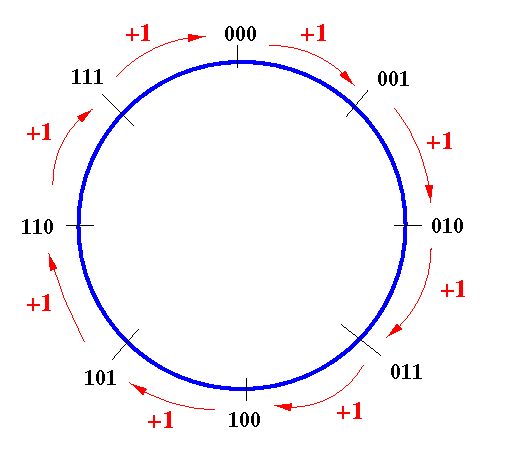
  Examples:
  - 000 + 1 = 001
  - 001 + 1 = 010
  NOTE:
  - 111 + 1 = 1000
    But you only have 3 bits - so the result is: 000
- The following figure shows how the binary number changes when you subtract the value 1 to a 3 bit binary number:
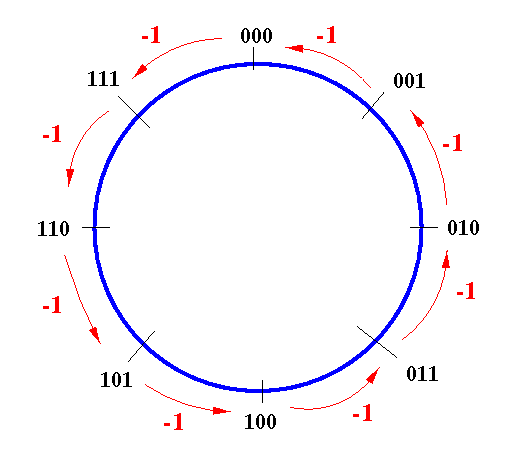
  Examples:
  - 111 - 1 = 110
  - 110 - 1 = 101
  NOTE:
  - 000 - 1 = ?
    You have to borrow from an imaginary 1 to the left of the number, i.e.:
    the result is: 111
- The 2's complement encoding method using this fact to encode the signed values (so that the add and subtract operation will remain "natural"):
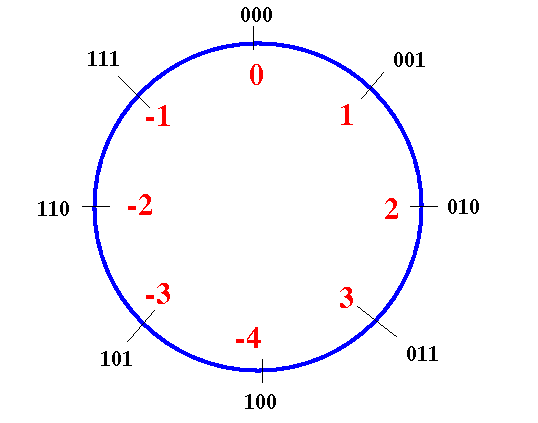
- The 3 bit 2's complement encoding scheme is:
- NOTE:
  - With 3 bits, we can represent only values between [-4, 3]
  - With n bits, we can represent values between [-2ⁿ, 2ⁿ-1]

The 8 bit 2's complement encoding method

The smallest number of bits that the computer can use is 8 bits
With 8 bits, we can values between [-2⁷, 2⁷-1] = [-128, 127]

The 2's complement encoding scheme represents approximately the same number of positive and negative values.

Hence, 8 bit 2's complement encoding method represents these values:

Code Value ================ 10000000 -128 <--- smallest negative value with 8 bits (-2⁷) 10000001 -127 ..... 11111000 -8 11111001 -7 11111010 -6 11111011 -5 11111100 -4 11111101 -3 11111110 -2 11111111 -1 00000000 0 00000001 1 00000010 2 00000011 3 00000100 4 00000101 5 00000110 6 00000111 7 00001000 8 ..... 01111111 127 <--- largest positive value with 8 bits (2⁷-1)

Again, to use 2s complement code, you need to know how to convert a value to 2s complement and vice versa

Encoding and Decoding in 2s complement codes

Look at the following table carefully to discover the coding & decoding method:

2's compl Value Compare with: Value Binary number system ================ ============================= 10000000 -128 128 10000000 10000001 -127 127 01111111 ..... 11111000 -8 8 00001000 11111001 -7 7 00000111 11111010 -6 6 00000110 11111011 -5 5 00000101 11111100 -4 4 00000100 11111101 -3 3 00000011 11111110 -2 2 00000010 11111111 -1 1 00000001 00000000 0 00000001 1 1 00000001 00000010 2 2 00000010 00000011 3 3 00000011 00000100 4 4 00000100 00000101 5 5 00000101 00000110 6 6 00000110 00000111 7 7 00000111 00001000 8 8 00001000 ..... 01111111 127 127 01111111

Notice that:

2s complement representation for positive values is same as that used in binary number system

Example:

00000000 00000001 1 00000010 2 00000011 3 00000100 4 00000101 5 <----- Representation --------------- 00000101 -> 4 + 1 = 5 ^ ^ ^ | | 4 1

2s complement representation for negative values added to the binary number for its absolute value is equal to 100000000.

Example:

11111010 -6 11111011 -5 <----- 11111100 -4 11111101 -3 11111110 -2 11111111 -1 00000000 0 11111011 = representation for -5 + 00000101 = representation for 5 (absolute value of -5) ------------- 100000000

These observations will help you understand the conversion procedures below.

Converting a value v to its 2's complement code:

If value v is positive, then:
- the 2's complement code is the same as its representation in the binary number system

If value v is negative, then:

First, obtain the binary number representation x for -v (note: -v is positive !)
Then, compute 100....000 - x, where the number 100....000 has exactly the same number of 0's as the number of bits in x.

Example:

 v = 7     The value is positive, so:
           (1) Binary number representation is: 111

           (2) 8 digit 2's complement representation is: 00000111
               16 digit 2's complement representation is: 0000000000000111
	       and so on...

 v = -7    The value is negative, so:
	   (1) Binary number representation for 7 is: 111

	   (2a) 8 digit 2's complement representation for 7 is: 00000111

	   (3a) 8 digit 2's complement representation for -7 is: 

			       100000000
			     -  00000111
			     -----------
				11111001


	   (2b) 16 digit 2's complement repr. for 7 is: 0000000000000111

	   (3b) 8 digit 2's complement repr. for -7 is: 

			       10000000000000000
			     -  0000000000000111
			     -----------
				1111111111111001

Converting a 2's complement code c to a signed value

If the encoding c begins with 0, it encodes a positive value and the value is "face value" in binary (but you will still need to convert it to decimal to be "comprehended" by humans)

If the encoding c begins with 1, it encodes a negative value and its absolute value is equal to 100...000 - c in binary (which again you will need to convert it to decimal to be "comprehended" by humans)

Example:

 code c = 00010010 -> it is a positive number
		      the value = 00010010 in binary

		      Convert to decimal:  0  0  0  1  0  0  1  0
						   16  +     2     = 18
		      Value = 18

 code c = 11101110 -> it is a negative number...

		      (1) Compute:      100000000 
				      -	 11101110
				      -----------
					 00010010 

		      (2) the absolute value of the negative value
			  is equal to 00010010 (binary), which is equal
			  to 18 (decimal)

		      (3) Since the value is negative, the value represented
			  by 11101110 is: -18 !

NOTE: from the examples above:
- 00000111 represents 7
  11111001 represents -7
- 00010010 represents 18
  11101110 represents -18
that:
to negate a value, you must subtract the representation by 1000...000

NOTE: there is an easier way to negate a 2s complement code:

Example: negate 7

    100000000        
   - 00000111 (= 7) 
  -----------
     11111001 (= -7)

   100000000 - 00000111 = (1 + 11111111) - 00000111
		        = 1 + (11111111 - 00000111)    [easy subtraction !]
			= 1 + 11111000

Summary, to negate a 2s complement representation:

Flip every bit in the 2s complement representation
Add 1 to the result

Example:
	As you saw above:    00010010 represents +18

        To get the representation for -18, you can do this:


	(1) Flip each bit:      00010010 -> 11101101

	(2) Add 1 to result:    11101101
			      +        1
			      ----------
				11101110

   which is - as you saw above - the representation for -18

Properties of 2's complement encoding:
- Only one representation for ZERO (check for yourself)
- Operations are "natural" - see examples below

Adding 2's complement numbers:

               Values        8 digit 2's compl repr
Adding 2 
positive           5                 00000101
values          +  9               + 00001001
                -----              ----------
                  14                 00001110  -> 8 + 4 + 2 = 14

Adding  
positive +         5                 00000101
negative        + -9               + 11110111
                -----              ----------
                  -4                 11111100 -> represents -4


Adding  
negative +        -5                 11111011
positive        +  9               + 00001001
                -----              ----------
                   4                 00000100 -> represents 4

Adding 2 
negative          -5                 11111011
values          + -9               + 11110111
                -----              ----------
		 -14                 11110010 -> represents -14

Subtracting 2's complement numbers:

               Values        8 digit 2's compl repr
Subtract 2 
positive           5                 00000101
values          -  9               - 00001001
                -----              ----------
                  -4                 11111100 -> represents -4

Subtract  
positive -         5                 00000101
negative        - -9               - 11110111
                -----              ----------
                  14                 00001110 -> represents 14


Subtract  
negative -        -5                 11111011
positive        -  9               - 00001001
                -----              ----------
                 -14                 11110010 -> represents -14

Subtract 2 
negative          -5                 11111011
values          - -9               - 11110111
                -----              ----------
		   4                 00000100 -> represents 4

Overflow

What is "overflow":
- Using 8 bits, we can represent the binary values between -128 and 127
- Computer operation manipulate (change) the representation
  For example:
```
	00000011   <---- representation for the value *** (3)
      +	00000101   <---- representation for the value ***** (5)
     ------------
	00001000   <---- representation for the value ******** (8)
```
- When the result of some operation on byte representations falls outside this range, then the value that is represented by the result is different from the correct value.
- This phenomenon is called overflow
- Overflow is a part of our daily life now that the computer is an integral part of our society and you should be aware of this phenomenon so you do not get caught by surprise...
Here is a program that demonstrates the overflow phenomenon: click here DEMO
- Try entering 1 + 1
- and then: 127 + 1 (this will cause an overflow)
- Do you understand why there is overflow at 127 using byte variables ??
The following program is the same as the previous one, except I have added a function to print out the binary representation of the values.
You can use this program to see why the program prints certain results: click here DEMO
Computer can manipluate integers of various lengths:
- 8 bits (byte type in Java, char type in C, C++)
- 16 bits (short type in Java, C and C++)
- 32 bits (int type in Java, C and C++)
- 64 bits (long type in Java, C and C++)
- 128 bits (long long type in C and C++)
- This program shows the effect of using more bits: click here DEMO
Other types of variables also have overflow problems, just later...
- short type variables will overflow at around 32000 (2¹⁵)
- int type variables overflow at around 2 billion (2³¹)
- Use the previous demo program to verify.
Changing the number of bits in the 2's complement representation
- The computer can use different numbers of bits to represent integer quantities:
  - byte (very short integer, values between -127 and 128)
  - short integer (values between -32767 and 32768)
  - (ordinary) integer (values between -2³¹ and 2³¹ - 1)
  - long integer (values between -2⁶³ and 2⁶³ - 1)
- Sometimes, the programmer needs to convert a byte to a short or a short to an integer in the program.
- This kind of operations is called a type conversion
  A data type is a certain data representation used in the computer
  The various kinds of integer representations (byte, short, int and long) are considered as different data representations
- When the computer computer needs to convert (change) from one represention to another representation, the key of the change must be that: the value of BOTH representation MUST BE EQUAL (because the value is intrinsic and does not change)

Sign extension (widening conversion):

Notice that:
- 8 bit 2s compl. repr. for 7 is: 00000111
- 16 bit 2s compl. repr. for 7 is: 0000000000000111
- 8 bit 2s compl. repr. for -7 is: 11111001
- 16 bit 2s compl. repr. for -7 is: 1111111111111001
To obtain the representation for the same value using more bits, the computer must "extend" the left most bit.

Example

     int i;
     short s;

     s = 9;   <---- s is assigned 0000000000001001
     i = s;   <---- assign an 16 bit integer to a 32 bit integer
                    (1) 0000000000001001 is sign-extended to:
		        00000000000000000000000000001001
		    (2) Then the value is store in variable i

     s = -9;  <---- s is assigned 1111111111110111
     i = s;   <---- assign an 16 bit integer to a 32 bit integer
                    (1) 1111111111110111 is sign-extended to:
		        11111111111111111111111111110111
		    (2) Then the value is store in variable i

Narrowing conversion (casting):

Narrowing conversion is when you convert a value from a "longer" representation to a "shorter" representation.

Example:

     int i;
     short s;

     i = 9;   <---- i is assigned 00000000000000000000000000001001
     s = i;   <---- assign an 32 bit integer to a 16 bit integer
                    (1) 00000000000000000000000000001001 is 
			truncated to 0000000000001001
		    (2) Then the value is store in variable s

     i = -9;  <---- i is assigned 11111111111111111111111111110111
     s = i;   <---- assign an 32 bit integer to a 16 bit integer
                    (1) 11111111111111111111111111110111 is 
			truncated to 1111111111110111
		    (2) Then the value is store in variable i

Narrowing conversion (truncation) may result in a represention for a value that is different than the original value:
i = 90000; i is assigned 00000000000000010101111110010000 s = i; (1) 00000000000000010101111110010000 is truncated to 0101111110010000 (2) assigned to s Problem: s represents 24464, (some bits lost !)
Program showing narrowing conversion: click here DEMO

The following program showing what happens when you convert:
- byte -> short or int
- short -> byte or int
- int -> byte or short
Get the program here: click here DEMO
- There are no problems from byte -> short or int
- Try entering 89 and (restart program) 1000 as a short, you will see overflow in the byte variable
- Try entering 89, (restart program) 1000 and (restart again) 80000 as int, you will see overflow in the byte variable for 1000, and overflow in short and byte for 80000.