- Given a number of video objects
- Choose the
number of fragments K
in which each video object will be divided.
-
Divide each video object into
K
fragments where the size of fragment i+1 is:
Di+1 = f * Di
- Based on various system parameters, we will choose
f to be at most:
B f <= ---- MK - The size of fragment i+1 is not easy to
determine; since it is determined
indirectly
by first choosing the parameter
K
(and computing
f
using
K)
- As a result, the sizes of the fragments resulting in the Pyramid Broadcasting method is unpredictable...
- Given a number of video objects
- "Choose" the
number of fragments K
in which each video object will be divided.
(I keep using the work "choose" because I want to relate to the Pyramid Broadcast method.
Yet, I put the word "choose" is in quotes, because, we don't really have a choice - we always have: K = B/M)
- Divide video into K fragments
- Unlike
Pyramid Broadcasting,
the relationship between
the size of fragment i+1
and the size
of the previous fragment i
is
pre-determined
in
Skyscraper Broadcasting :
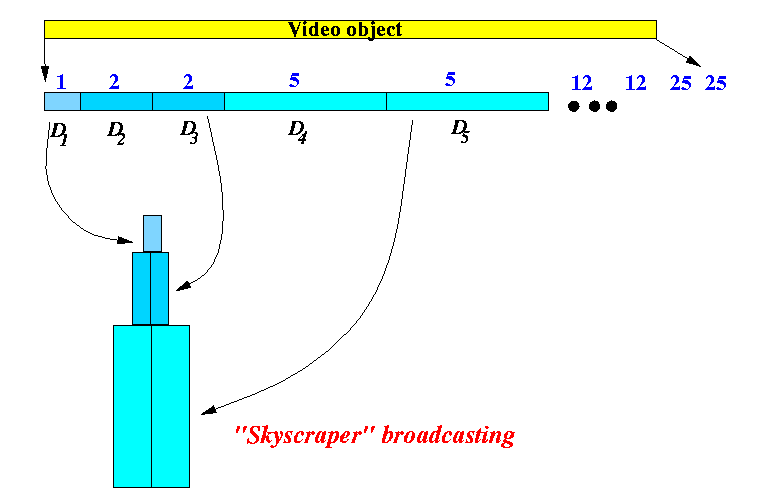
- D1 = 1 * D1
- D2 = 2 * D1
- D3 = 2 * D1
- D4 = 5 * D1
- D5 = 5 * D1
- D6 = 12 * D1
- D7 = 12 * D1
- D8 = 25 * D1
- D9 = 25 * D1
- and so on... (this relationship will be discussed below)
- Notice that in
Skyscraper Broadcasting ,
we know the
relative size
in advance :
-
In Pyramid Broadcasting,
the relative size is
variable (f)
- and it can change...
- In Skyscraper Broadcasting, the relative size are constant (2, 5, 12, 25, etc) - and they CANNOT change...
-
In Pyramid Broadcasting,
the relative size is
variable (f)
- and it can change...
- Result: less surprise about the size of each fragment....
- In Skyscraper Broadcasting, we have (almost) total control on how fast the fragment size grows.....
- Skyscraper Broadcasting has
lower disk storage
requirement than Pyramid Broadcasting
- Skyscraper Broadcasting has lower lower disk bandwidth requirement than Pyramid Broadcasting
- Channel efficiency
is not as good as Pyramid broadcasting....
(I.e., Skyscraper Broadcasting need to use more channels than Pyramid Broadcasting to broadcast the same set of videos
(you don't get something for nothing, also known as "The Law of Conservation of Misery" in Mathematics)
(I personally find this technique exceptionally beautiful...)
- B = The bandwidth of the entire channel
- M = number of video objects
- D =
length of one video object (all video objects have same length)
- B and D have been normalized to use as unit the consumption rate video (each unit is b bits/sec)
- Similar to
Pyramid Broadcasting,
each video object in
Skyscrapper Broadcasting is also
partitioned
into
K fragments
- The fragments also have
increasing sizes...
But the sizes do not increase exponentially, rather, "quasi" linearly:
- Let
Di
denotes the size of the video fragment
i
Then:
- (D1 = 1 * D1)
- D2 = 2 * D1
- D3 = 2 * D1
- D4 = 5 * D1
- D5 = 5 * D1
- D6 = 12 * D1
- D7 = 12 * D1
- D8 = 25 * D1
- D9 = 25 * D1
- and so on...
- More precisely, the size of fragment i is:
-
Di = f(i) * D1
where f(1) = 1 is defined as:
- f(1) = 1
- f(2) = 2
- f(3) = 2
- f(n) = 2 f(n-1) + 1, if n is divisible by 4
- f(n) = f(n-1),
if n-1 is divisible by 4
- f(n) = 2 f(n-1) + 2, if n is even but not divisible by 4
- f(n) = f(n-1), if n-1 is even but not divisible by 4
- f(1) = 1
- If you have a hard time with the formulas, just remember this sequence:
- Start with 1, 2, 2, then repeat:
- double it and add 1
- same
- double it and add 2
- same
- double it and add 1
- same
- double it and add 2
- same
- etc...
Result: 1, 2, 2, 5, 5, 12, 12, 25, 25, 52, 52, 105, 105, 212, 212, ...
- Start with 1, 2, 2, then repeat:
- Just a point of interets:
-
The name Skyscraper
Broadcast is derived from the
look
of the structure when
you stack the fragments one on top of the other...
the resulting structure that you get looks like a skyscraper... as shown in the following figure
- The Skyscraper Broadcasting method consists of:
- Transmission algorithm used by the sender
- Receive algorithm used by each receiver.
- Just like the
Pyramid Broadcasting method,
the
Skyscraper Broadcasting method
transmits
each fragment
in
one single channel
(And will therefore transmit the video object in K channels, since one video object is partitioned into K fragments)
- The transmission medium has a total bandwith of
B
(normally by the consumption rate
b bps)
- The transmission medium is partitioned into
B channels,
each channel with a data rate of
1
(that means that each channel transmits at
the consumption rate
b bps)
In other words:
The transmission rate on each (sub)channel in Skyscraper Broadcasting is equal to the consumption rate This is exactly the same as how cable/satelite channels likes to transmit the video !
- The
B channels
are divided evenly among the
M video objects
- Thus each video object will receive:
- B/M channels
for its own use.
- To use up these B/M
channel,
each video object is divided into this number
of fragments.
In other words:
K = B/M
fragments, and each fragment is sent on its own channel
- As I mentioned before,
the number of fragments
K
is not chosen,
but determined as
K = B/M
from the video parameters
- Recall,
that the sizes of the fragments are:
- D1 = 1 * D1
- D2 = 2 * D1
- D3 = 2 * D1
- D4 = 5 * D1
- D5 = 5 * D1
- D6 = 12 * D1
- D7 = 12 * D1
- D8 = 25 * D1
- D9 = 25 * D1
- ....
- DK = ... (stop at K because there are K fragments
- The length of the
first fragment
can be determined from the following relation:
-
D1 + D2 + .... + DK = D
D1 + 2 D1 + 2D1 + 5 D1 + 5 D1 + .... = D
Each of the variables Di can be expressed as some multiple of D1,
By substituing all Di as some multipl of D1, we can find D1 (because D is given - it is a parameter of the problem)
- After dividing each video object into
K = B/M
fragments,
each fragment will be broadcast
repeatedly on its own channel
(just like Pyramid Broadcasting)
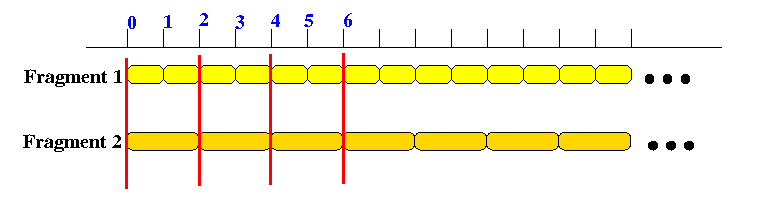
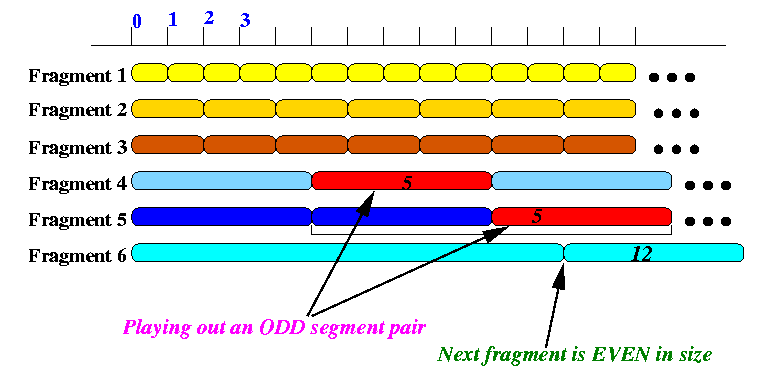
- Example:
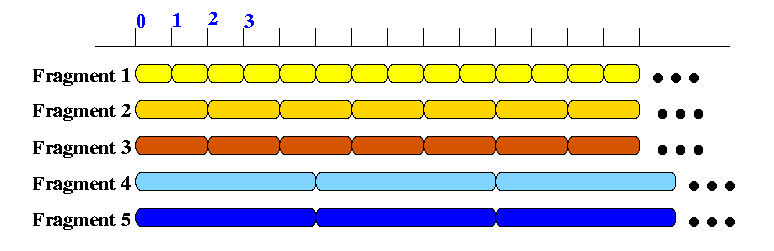
- The example shows one video object divided into 5 fragments
- Fragement 1 has a certain size (computed as decribed above)
- Fragement 2 and 3 has a size that is twice that of fragment 1
- Fragement 4 and 5 has a size that is five times that of fragment 1
(For clarity, I have display a scale at top that has a unit the size of video fragment 1.)
- The fragments:
- D1 = 1 * D1
- D4 = 5 * D1
- D5 = 5 * D1
- D8 = 25 * D1
- D9 = 25 * D1
- ....
are called odd sized fragments (because they are an odd multiple of D1).
- The fragments:
- D2 = 2 * D1
- D3 = 2 * D1
- D6 = 12 * D1
- D7 = 12 * D1
- ...
are called even sized fragments (because they are an even multiple of D1).
- The
Skyscraper receiver
consists of
3 independent processes:
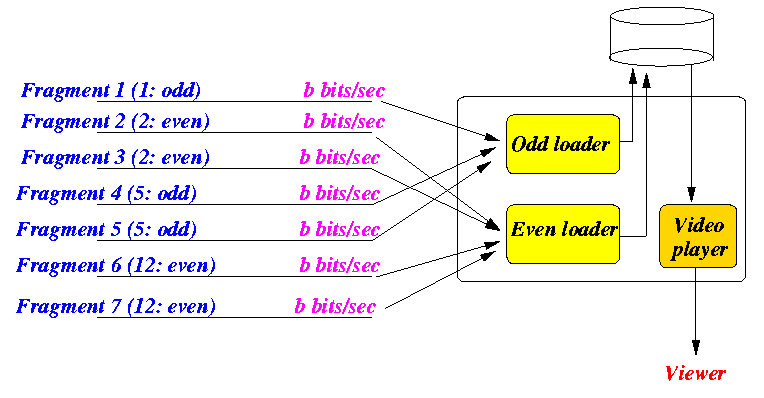
- An
odd loader
that tunes to channels that broadcast
odd sized
fragments.
The odd loader downloads odd sized fragments one after the other in sequence.
- An
even loader
that tunes to channels that broadcast
even sized
fragments.
The even loader downloads even sized fragments one after the other in sequence.
- A video player that plays out the fragments in the proper order
(this component will not be discussed, the key to the operation of Skyscraper Broadcasting are the "odd" and "even" loaders)
- An
odd loader
that tunes to channels that broadcast
odd sized
fragments.
- NOTES:
- The
odd loader
and the
even loader
operate
independently
The skyscraper receiver can simultaneously download from 2 channels (while at the same time playing out the video).
- Because the
odd loader
and the
even loader
are
independently,
an odd sized fragment and an even sized fragment
can
start their download
simultaneously
- Since there is only
ONE odd loader
and
ONE even loader,
TWO odd sized fragments or
TWO even sized fragments
CANNOT start their download simultaneously
- A fragment in Skyscraper Broadcast can only be received starting from the beginning (i.e., not from the middle) - this simplifies the download method
- The
odd loader
and the
even loader
operate
independently
- If you are already convinced that the Skyscraper works,
then I have a bridge for sale :-).
- The $64,000 question that we have to ask is:
Can the receiver download and display the entire video object uninterrupted ? By that we mean: once the receiver start downloading fragment 1 of the video, can he download fragment 2 in time, and then fragment 3, and so on ?
- To obtain the entire video uninterrupted,
the data of the next fragment must be available
(either it has been pre-fetched or it can be downloaded immediately)
when the current segment is completely played out...
- Before I show the formal proof (from the paper click here ), I will give you some idea what the scheme is doing using various scenarios....
- The following picture shows a receiver that starts downloading
the video between "times" 4 and 5:
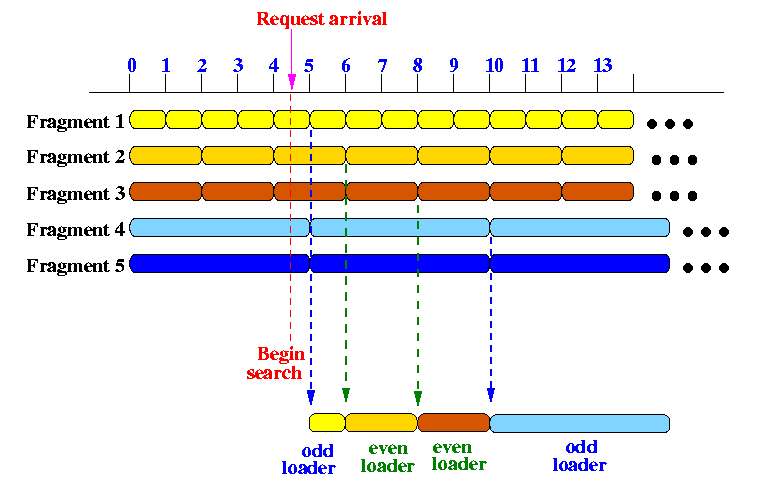
- Both the
odd loader
and the
even loader
begin searching for their fragments at the start time.
- The
odd loader
starts downloading
fragment D1
(and the player start displaying)
at time 5.
- The
even loader
starts downloading
fragment D2
at time 6.
At time 6, odd loader starts looking for fragment fragment D4 (which it finds at time 10). - The
even loader
finished downloading
fragment D2
at time 8 and
immediately
starts downloading
fragment D3
(because
the start of
fragment D3
coincides
with the end of
fragment D2 -
this is
planned
because these
pairs of fragments
have the same size !!!)
- The
even loader
finished downloading
fragment D3
at time 10 and
luckily
the
odd loader
starts downloading
fragment D4
at time 10
The viewing of the video is uninterrupted
- Both the
odd loader
and the
even loader
begin searching for their fragments at the start time.
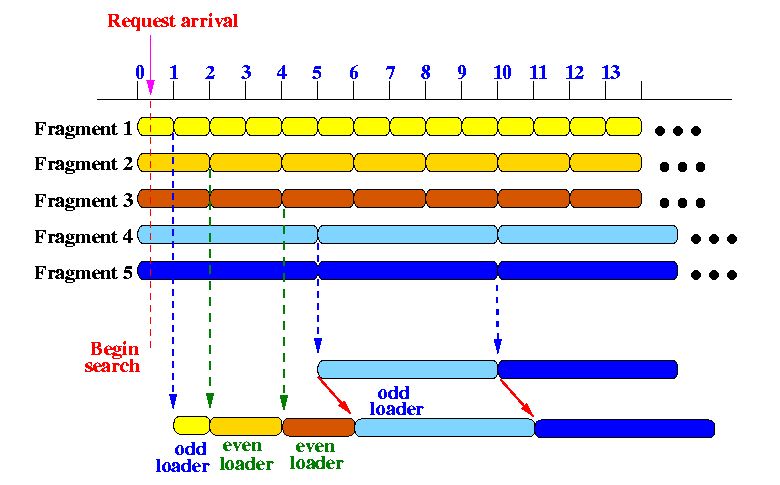
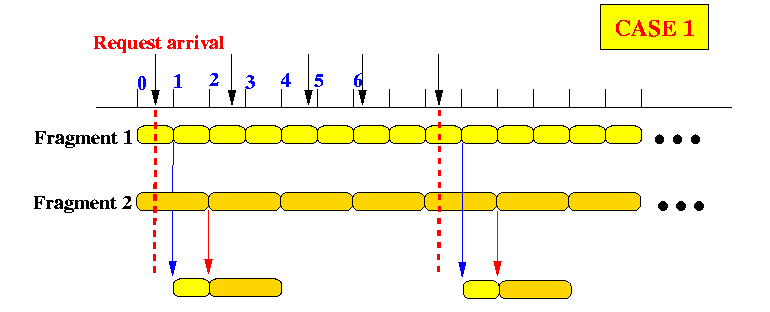
- The following picture shows a receiver that starts downloading
the video between "times" 0 and 1:
- Both the
odd loader
and the
even loader
begin searching for their fragments at the start time.
- The
odd loader
starts downloading
fragment D1
(and the player start displaying)
at time 1.
- The
even loader
starts downloading
fragment D2
at time 2.
Also, at time 2, odd loader finished downloading fragment D1 and starts looking for fragment fragment D4 (which it finds at time 5). - The
even loader
finished downloading
fragment D2
at time 4 and
immediately
starts downloading
fragment D3
(because
the start of
fragment D3
coincides
with the end of
fragment D2 -
this is
planned
because these
pairs of fragments
have the same size !!!)
- The
even loader
finished downloading
fragment D3
at time 6 and
luckily
the
odd loader
started downloading
fragment D4
at time 5 - some video will be buffered as depicted
in the following figure:
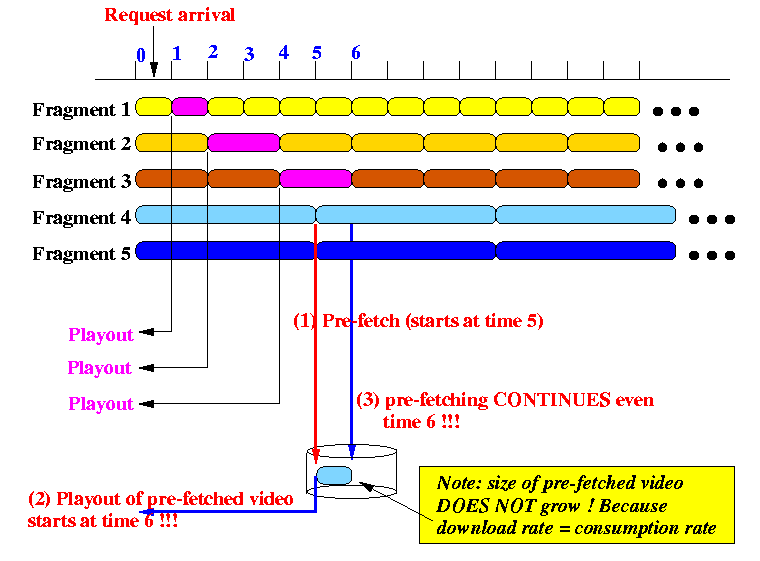
The viewing of the video is again uninterrupted
(The pre-fetch technique is not new, we have seen that in Pyramid broadcasting...)
- Both the
odd loader
and the
even loader
begin searching for their fragments at the start time.
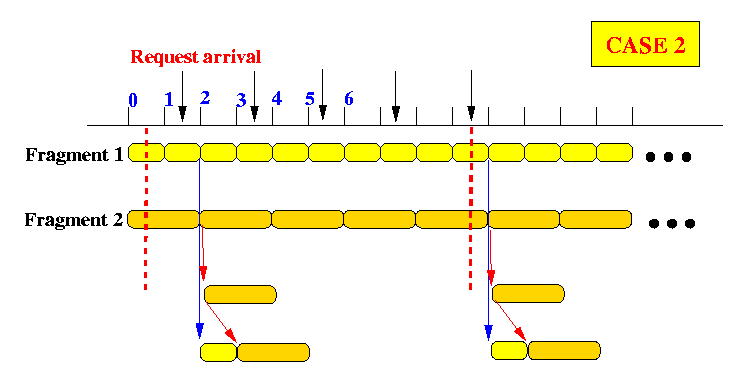
- The following picture shows a receiver that starts downloading
the video between "times" 1 and 2:
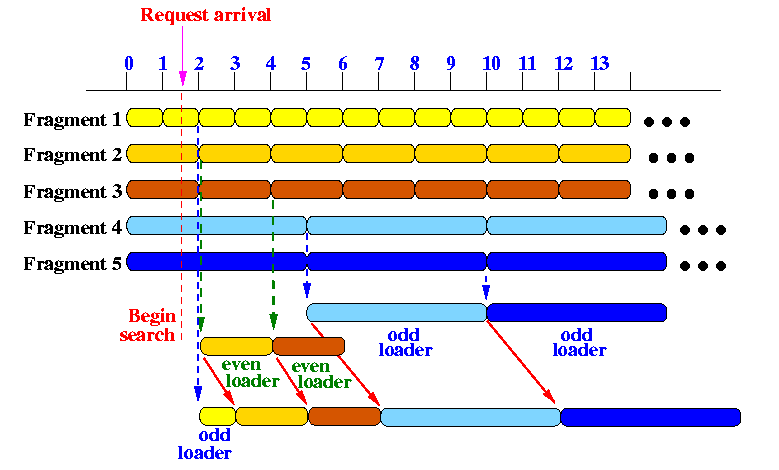
- Both the
odd loader
and the
even loader
begin searching for their fragments at the start time.
- The
odd loader
starts downloading
fragment D1
(and the player start displaying)
at time 1.
The even loader also starts downloading fragment D2 (and the player start displaying) at time 1 (video fragment will be buffered). - At time 2,
odd loader
finished downloading (and displaying)
fragment D1
and
starts looking for fragment
fragment D4
(which it finds at time 5).
Meanwhile, stored video from fragment D2 are shown. - The
even loader
finished downloading
fragment D2
at time 4 and
immediately
starts downloading
fragment D3
(because
the start of
fragment D3
coincides
with the end of
fragment D2 -
this is
planned
because these
pairs of fragments
have the same size !!!)
- The
even loader
finished downloading
fragment D3
at time 6 and
luckily
the
odd loader
started downloading
fragment D4
at time 5 - some video will be buffered as depicted
in the following figure:
The viewing of the video is again uninterrupted
(The pre-fetch technique is not new, we have seen that in Pyramid broadcasting...)
- Both the
odd loader
and the
even loader
begin searching for their fragments at the start time.
- Is the receiver always able to obtain the next fragment
when the current fragment is finished ???
- In other words:
- Will the start of the next fragment always be broadcast during the playback period of the current fragment ?
- The above question must be answered before the technique is
deem correct
(If there is a possibility that a receiver cannot playout the video continuously, the method is flawed and nobody will use it... reason is simple, you will lose customers and enter bankruptcy court faster than Speedy Gonzales...)
|
OK, after seeing 3 scenarios, let us go back to
the $6,000,000 question is:
|
- The proof that
the receiver in Skyscrapper Broadcasting
can always receive the video uninterrupted once
it start downloading
is not as "clean" as the pyramid scheme
- The proof has to consider many different cases -
so I want to prepare you for the proof with an overview
of the case considered.
- The cases considered are:
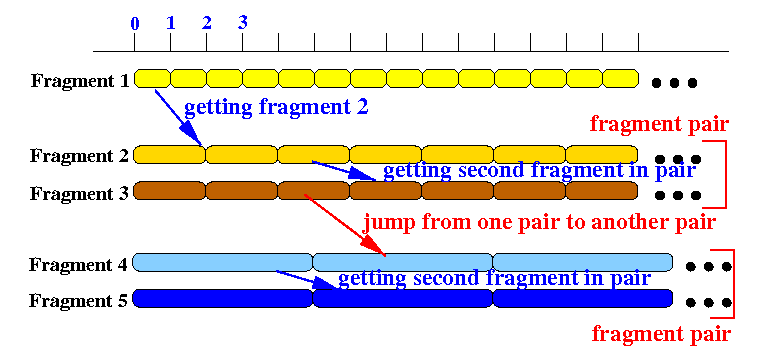
- Getting fragment fragment D1
- Getting fragment fragment D2
- Getting the
second fragment
in a
fragment pair
- Getting the
first fragment
in a
fragment pair
- Case 1: even size fragment -->
odd size fragment
- Case 2: odd size fragment --> even size fragment
- Case 1: even size fragment -->
odd size fragment
- Simply
wait
until the start of the next time that the first fragment
will be broadcast.
- This is also the access time of the video
-
Fact:
The size of
fragment D2
is always twice the size of
fragment D1
- Assuming that the transmission
of the fragments starts at time 0 and a "slot unit"
is the time to transmit
fragment D1,
then:
The start of fragment D2 (or any of the even sized fragments) ALWAYS begins in an EVEN slot index !!! Example:
- Because the size of
fragment D2
is
twice as large
as
fragment D1,
there are
exactly two different ways
to
transit
from fragment 1 to fragment 2:
Case 1: Request arrives after an even "time" point but before an odd "time" point
- Both the
odd and even loader
will start before an
odd "time" point
- The next
"time" point
reached will be
odd
and the
odd loader
will start downloading (and displaying)
fragment D1
The even loader will not start yet.
- The odd loader
will finish at the next
"even" time point,
at which time
the even loader
will also find and download the start of
fragment D2
- So no break when during the transition from fragment D1 to fragment D2
Case 2: Request arrives after an odd "time" point but before an even "time" point
- Both the
odd and even loader
will start before an
even "time" point
- The next
"time" point
reached will be
even , so:
- the odd loader
will start downloading (and displaying)
fragment D1
because fragment D1
is started on every "time" point
- the even loader will also start downloading (and buffering) fragment D2 because fragment D2 is started on every even "time" point
- the odd loader
will start downloading (and displaying)
fragment D1
because fragment D1
is started on every "time" point
- So no break when during the transition from fragment D1 to fragment D2
- Both the
odd and even loader
will start before an
odd "time" point
- If you look carefully at the relative fragment sizes:
1, 2, 2, 5, 5, 12, 12, 25, 25, 52, 52, 105, 105, 212, 212, ....you see that:-
Except for fragment 1, all other fragments are in pairs
- Fragment pairs have equal length (and both are odd sized or both are odd sized)
-
Except for fragment 1, all other fragments are in pairs
- It is easy to see that when
the
odd or even loader
has finished downloading the
first fragment of a pair,
then the
same loader
can download the
second fragment of the pair,
without any delay:
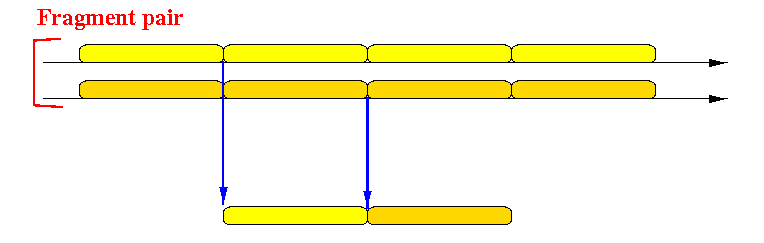
(because the time of the end of the first fragment is also the start of the next fragment !!!)
- So the
second fragment of the pair
can be downloaded and displayed without break.
So we have covered these fragments:
1, 2, 2, 5, 5, 12, 12, 25, 25, 52, 52, 105, 105, 212, 212, .... ^ ^ ^ ^ ^ ^ ^ | | | | | | | These fragments can surely be displayed without break.
- There are
2 different
video stream transition
situations that we need to consider:
Current stream Next stream Example -------------- ----------- ------- even size odd size 2, 2, -> 5, 5, ..., 12, 12, -> 25, 25 odd size even size 5, 5, -> 12, 12, ..., 25, 25, -> 52, 52We will look at each of the cases separately...
- The following figure depicts a transition situation where:
- The receiver has just finish playing the
second fragment
of an even sized fragment pair
- Question:
-
Will the
odd loader
be able to start downloading the next
odd sized fragement
before the
second fragment of the
even sized fragment pair finishes
displaying
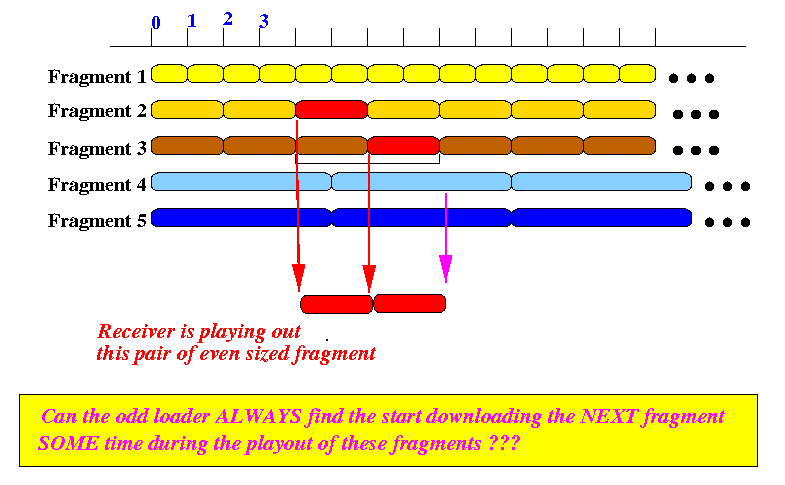
Important observation:
- If the even sized fragment is A, the size of
the odd sized fragment is 2A + 1
- The receiver will be able to get the odd sized
fragment, it
the start of the odd sized
fragment is broadcasted
sometime
during the playback period of the
current even sized fragment
or the
previous even sized fragment !
(Fragments that we are considering comes in PAIRS. Both (even) pairs are of the same size and will be downloaded by the even loader. While the even loader is downloading the 2 even fragments, the odd loader will be on the look out for the next odd fragment !)
Let us explore if (and how) the receiver in general that has finished playing an even size fragment pair will be able to obtain the next odd value size segment in time...
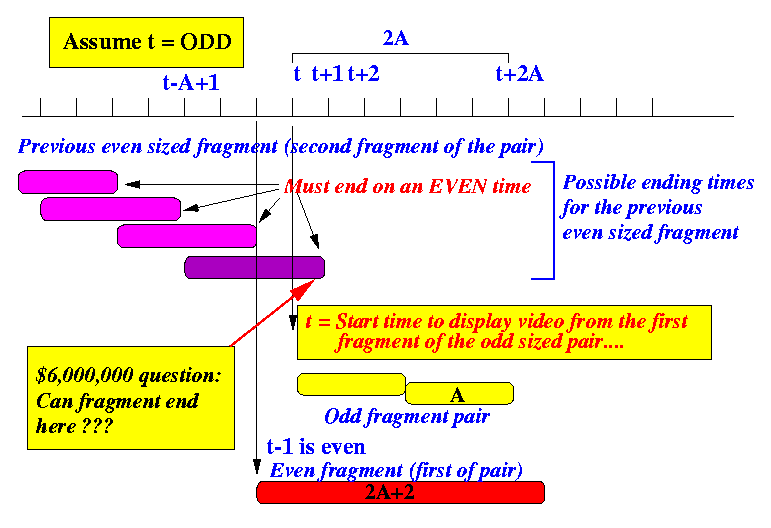
- Definition:
Let t denote the playout time of the first fragment of the even value size fragment pair.
I.e., the video from the first fragment of the even fragment pair will be displayed at time t
The following figure shows the possible broadcast times of the odd size fragment during the period when the even fragment pair are being displayed:
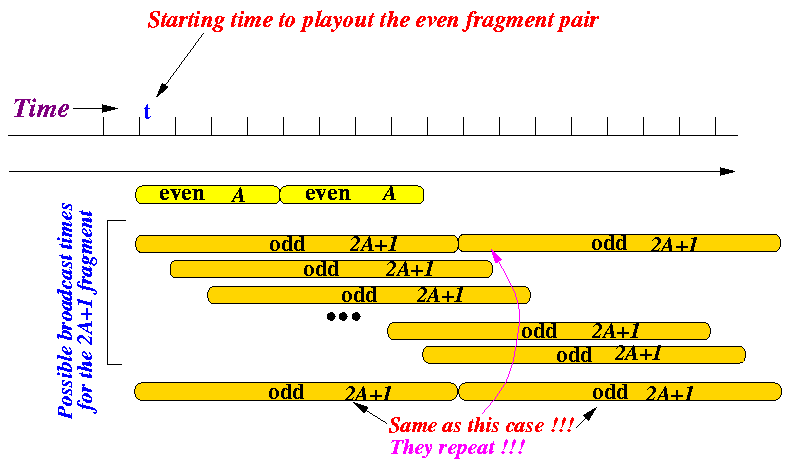
We can see that the start of fragment 2A+1 is encountered (exactly) once during the playout period of the two even (A) fragments:
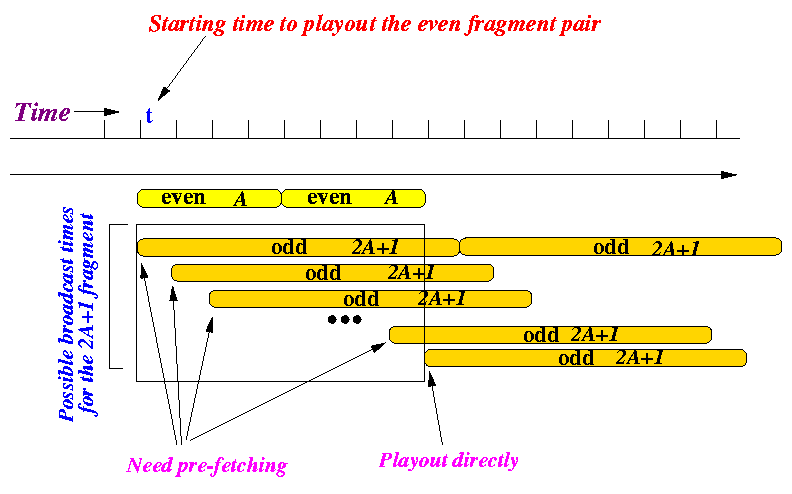
- In all cases, except one, the odd fragment 2A+1 need
to be pre-fetched.
- If the odd fragment 2A+1 is broadcast at time t+2A, the receiver can download the fragment and playout immediately (no pre-fetch).
- The receiver has just finish playing the
second fragment
of an even sized fragment pair
- Further comments:
- Note: just to make sure you understand what I meant
by "need pre-fetching", the following example shows
how the 2A+1 fragment is pre-fetched:
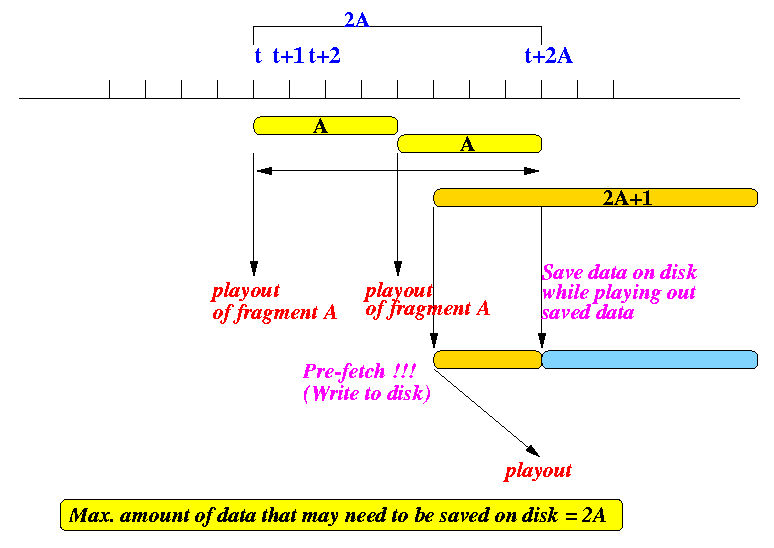
-
NOTE: to make sure you understand what's going on, here is
a hypothetical situation where the receiver cannot obtain
the next fragment
(I need to use a longer fragment
(2A+2) to make the point):
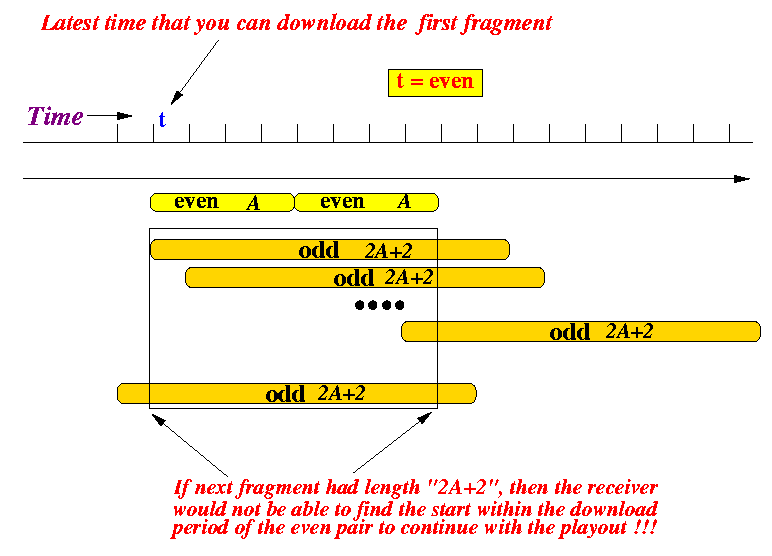
- Note in the figure that there exists the possibility that
the start of the 2A+2 fragment does not
begin within the playout period of the prior even fragment pair.
In such case, the receiver would not be able to obtain the next fragment when it starts playing the current fragment.
- Note in the figure that there exists the possibility that
the start of the 2A+2 fragment does not
begin within the playout period of the prior even fragment pair.
- Note: just to make sure you understand what I meant
by "need pre-fetching", the following example shows
how the 2A+1 fragment is pre-fetched:
- The receiver has just finish playing the
second fragment
of an odd sized fragment pair
- The next fragment (must) have a even value size
- If the odd sized fragment is A, the size of
the even sized fragment is 2A + 2
- The receiver will be able to get the even sized
fragment, it
the start of the even sized
fragment is broadcasted
sometime
during the playback period of the
current odd sized fragment
or the
previous odd sized fragment !
(Again, fragments that we are considering comes in PAIRS. Both (odd) pairs are of the same size and will be downloaded by the odd loader. While the odd loader is downloading the 2 odd fragments, the even loader will be on the look out for the next even fragment !)
- The total amount of time to play out a PAIR
of odd sized fragment is always even !!!
- The start time of the even fragment that the even loader is looking for is always an even time (e.g., 2, 4, 6, 8, etc) !!!
-
An early analysis...
If you followed the last discussion on how we tried to start the next fragment on all possible times within the transmission time of the fragment pair, you would think that in this case (when the receiver is receiving an odd sized pair and looking for an even sized pair), the receiver may not be able to download the even sized fragment in time....
Since the size of the even sized fragment is equal to 2A + 2, the following would be a situation where this 2A + 2 fragment does not begin within the playout time of the previous fragment pair:
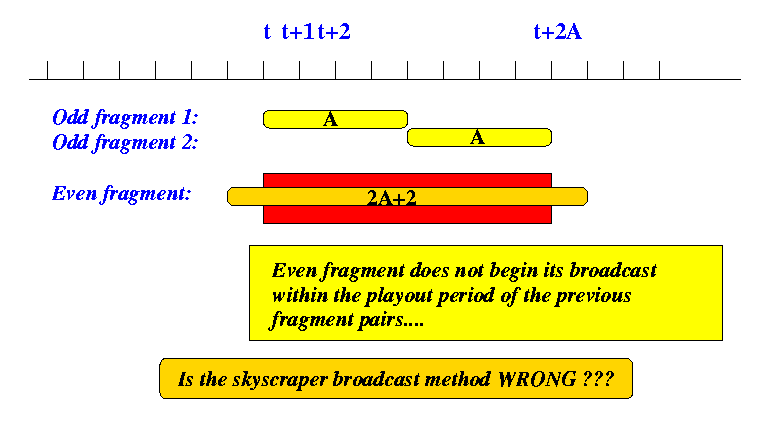
-
So is the sky-scraper broadcast scheme
INCORRECT ???
To show that the receiver can always obtain the even fragment after the odd fragment pair, we have to consider t = even and t = odd separately.
Case 1: t = even
- The following figure shows the possible broadcast times of the
even size fragment during the period when the odd fragment pair
are being displayed if t = even:
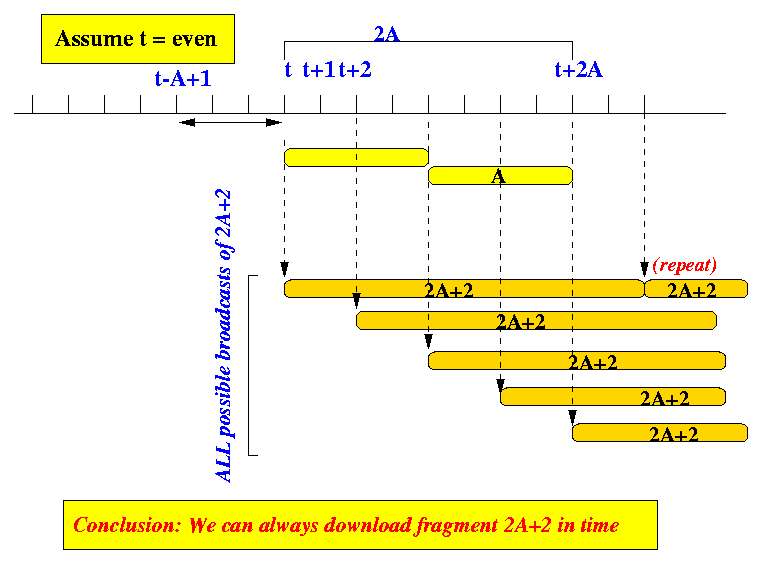
- Note that the starting time of the broadcast of an even fragment
is always even !!!
- There are A possible times that the 2A+2
can start (CHECK this fact ! --- length is 2A+2,
always begin at even time)
- We can see from the figure above that for every possible starting time of the fragment 2A+2, the start of a fragment 2A+2 is encountered (exactly) once during the playout period of the two odd (A) fragments.
Case 2: t = odd
- The following figure shows the possible broadcast times of the
even size fragment during the period when the odd fragment pair
are being displayed if t = odd
(t-1 = even):
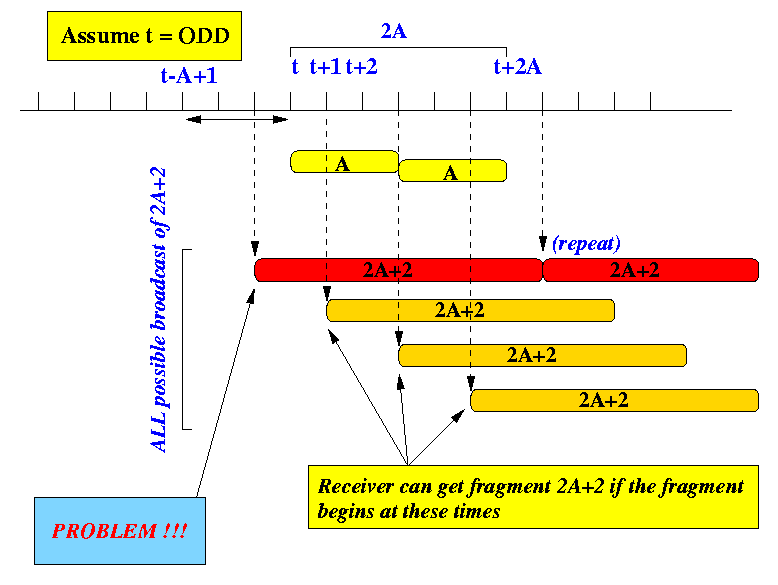
-
Note again that the starting time of the broadcast
of the first fragment of the even sized fragment pairs
is always even...
- There are again A possible times
that the 2A+2
can start (CHECK this fact ! --- length is 2A+2,
always begin at even time)
- We can see from the figure above
that for every possible starting time EXCEPT ONE
of the fragment 2A+2,
the start of a fragment 2A+2
is encountered (exactly) once during the playout period
of the two odd (A) fragments.
- So in those A - 1 cases,
the receiver will have no problem downloading
the 2A+2 fragment in time.
- But there is
one case
where the start of the first fragment of
the even sized fragment pairs is NOT encountered
during the transmission of the odd fragment pair, we
would have a BREAK in video...
Is our goose cooked in this case ?????
If not, how can be handle this particular situation.... ???
- The following figure shows the possible broadcast times of the
even size fragment during the period when the odd fragment pair
are being displayed if t = even:
The following figure depicts an example of a transition where:
|
Important observation:
|
|
Let us now explore if (and how) the receiver in general that has finished playing an odd sized fragment pair will be able to obtain the next even sized segment in time...
Again, let t be the starting display time of the first fragment of the odd sized fragment pair...
- Recall the problem case in
transition
from odd size fragment to even size fragment:

- The special case when the broadcast time of the even fragment
is t - 1 can be handled as follows:
- First: note that we are currently downloading an odd sized pair and
try to switch to an even sized pair....
so there must have been a preceeding even pair
that the even loader has downloaded:
1, 2, 2, 5, 5, 12, 12, 25, 25, 52, 52, 105, 105, 212, 212, .... ^^^^ ^^^^^^ ^^^^^^^^ - The operation of the even loader (and the odd loader also) is such
that
after finishing downloading an even sized fragment,
it can immediately tune to the
the next channel and download another
an even sized fragment....
-
The transmission time for even sized fragment pairs
not only starts at an even time but also
always ends at an even time
-
Consider now the latest possible time
that the even loader
finishes loading the second fragment in the previous
even sized fragment pair:
- The picture above depicts some ending times for downloading the
"previous" even sized fragment.
- We know for sure that the ending time is even
- We also know that is the ending time for downloading the
"previous" even sized fragment is
t + 1 or later,
then there will be a break in the video.
Why ? Well, the starting time to display the odd sized fragment A is t.
So, if the previous fragment did not complete downloading before time t (which would be the case if the ending time for downloading the "previous" even sized fragment is t + 1 or later), the video will surely not show up in time at time t !!!
- That's why the $6,000,000 question is:
can the ending time for downloading the
"previous" even sized fragment is
t + 1 or later ???
If the answer is "yes", our goose is cooked and we can pack up and go home...
If the answer is "no", you better convince the buyer of your system that it is so...
-
The answer is of course "yes", and the convincing argument
goes as follows:
- The size of the magenta color stream is even
- The size of the yellow color stream is odd
- So the situation we are looking at is: whether there is
a break in video when we are receiving an even
sized stream and transitioning to an odd
stream
- We have proved that in such a case,
there is no break in video delivery, see:
click here
- Therefore, the even loader
must have finished downloading
the "previous" even sized fragment at time
t - 1 or earlier
In any case, the even loader has finished in time to download the 2A+1 fragment that starts at time t - 1 !!!
- The size of the magenta color stream is even
- The picture above depicts some ending times for downloading the
"previous" even sized fragment.
- Therefore, the even loader can switch in time to download the next even fragment despite the fact that the beginning of the first fragment of the even sized fragment pair falls outside the display time interval of the odd-sized fragment pair.
- First: note that we are currently downloading an odd sized pair and
try to switch to an even sized pair....
so there must have been a preceeding even pair
that the even loader has downloaded:
- From the description of the skyscraper receiver, we can calculate the
maximum disk bandwidth needed...
- Recall that data rate of each channel is b bits/sec,
which is the same as the consumption rate (so video source sends
at the rate that is being consumed, just like cable/satelite)
- Therefore, the maximum disk bandwidth in Skyscraper is 3 x b bits/sec (writing 2 video streams while playing out video from disk)
- Receivers in skyscraper broadcast will be able to display the video without interruption.