---

Self-Clocked Fair Queueing: A Simple and Efficient approximation of WFQ

---

• The Problem with WFQ
  • The difficulty of WFQ according to Golestani:

  • Note:

    Parekh called his own method Packet Fair Queueing (PFQ) This scheme is commonly known as Weighted Fair Queueing (WFQ) The Fluid Fair Server (FFS) is also known as Fluid Fair Queueing (FFQ) This complexity of the FFS is in the fact that: Multiple packets receive service (transmission) simultaneously Computing the termination time of a packet transmission is very tedious (as we have seen in the previous 2 lecture notes)

    ---

    ---

  • Self-clocked fair queueing:

    Golestani presented an ingenious approximation of the WFQ scheme by approximating the virtual time system in WFQ The resulting packet scheduling method will be less accurate than WFQ It will not achieve the best possible approximation of the ideal FFS service. However: Achieving the best possible fairness is not the point of the reserach in providing Quality of Service in Computer Networks The goal is to develop an efficient algorithm that prvides a good approximation of the FFS service.

  ---

  ---

• Approximating of virtual clock in FFS

  • Virtual time update algorithm in WFQ:

    The speed of the Virtual Clock is equal to: ---- \ 1 Speed of virtual clock at real time t = > --- / wj ---- All active flows j at time real time t in a FFS system Difficulty: In WFQ, the Virtual Clock in continuously updated

    ---

  • Virtual time (clock) update algorithm in SCFQ:

    The speed of the Virtual Clock is approximately equal to: ---- \ 1 Approximate Speed of virtual clock at real time t = > --- / wj ---- All active flows j at time real time t in a SCFQ system Simplification 1: we do not keep track of how the FFS server processes the packets We only keep track of how the SCFQ server processes the packets Simplification 2: The virtual clock is updated once per packet transmission

    ---

    ---

  • $64,000 question:

    How can you approximate the Virtual Clock in the FFS server ???

  ---

  ---

• Approximating the Virtual clock in WFQ
  • Example 1:

    3 flows: w1 = 1/3 w2 = 1/3 w3 = 1/3            Packet arrivals: (3 packets from flow 1)             t = 0, len(p11) = 2 t = 1, len(p12) = 1 t = 2, len(p13) = 2            Virtual packet lengths: virtual len(p11) = 6 virtual len(p12) = 3 virtual len(p13) = 6

  • The packets are serviced as follows:

    Time stamps: p11 arrives, receives V(p11) = 6 ^ p12 arrives, receives V(p11) = 6 + 3 = 9 | ^ p13 arrives, receives V(p11) = 9 + 6 = 16 | | ^ | | | |--------+--------+--------+--------+--------+--------+------------> real time t=0 t=1 t=2 t=3 t=4 t=5 t=6 | | | | | V | V p12 finishes (V(p11) = 15) V p12 finishes (V(p11) = 9) p11 finishes (V(p11) = 6) Virtual time: VT(t) = 3 × t V(2)=6 V(3)=9 V(5)=15 |-----------------|--------|-----------------|--------------> virtual time

    Conclusion:

    When a single flow is continuously backlogged: the value of the virtual clock is equal to the time stamp of the packet in service at the moment when the packet finishes transmitting

  ---

  ---

• Ideal for an approximation of the Virtual Clock in the FFS server
  • Approxmation idea:

    Set the virtual time (clock) to the time stamp of the packet in service when the packet in service finishes service

    Example:

    packet px finishes service packet py finishes service (Vpx = A) (Vpy = B) | | | | V V |-------+-------+-------+-------+-------+-------+-------+----------> real time |---------------|-------------------------------|------------------> virtual time VT=A VT=B

    ---

  • $64,000 question:

    How about the other times ??? packet px finishes service packet py finishes service (Vpx = A) (Vpy = B) | | | | V V |-------+-------+-------+-------+-------+-------+-------+----------> real time |---------------|-------------------------------|------------------> virtual time VT=A ??? VT = ??? VT=B

    Answer from Gelestani:

    The virtual clock at other times remains unchanged: packet px finishes service packet py finishes service (Vpx = A) (Vpy = B) | | | | V V |-------+-------+-------+-------+-------+-------+-------+----------> real time |---------------|-------------------------------|------------------> virtual time VT=A <----- (VT = A) -----> VT=B

  ---

  ---

• The virtual clock function in SCFQ
  • Just like WFQ, the virtual clock function in SCFQ depends on the backlogged flows in the router

    ---

  • Example: previously studied arrival pattern

    Time stamps: p11 arrives, receives V(p11) = 6 ^ p12 arrives, receives V(p11) = 6 + 3 = 9 | ^ p13 arrives, receives V(p11) = 9 + 6 = 16 | | ^ | | | |--------+--------+--------+--------+--------+--------+------------> real time t=0 t=1 t=2 t=3 t=4 t=5 t=6 | | | | | V | V p12 finishes (V(p11) = 15) V p12 finishes (V(p11) = 9) p11 finishes (V(p11) = 6) WFQ's Virtual clock: VT(t) = 3 × t SCFQ's Virtual clock: V(2)=6 V(3)=9 V(5)=15 |-----------------|--------|-----------------|--------------> virtual time <------- 6 ------><-- 9 --><------- 15 ------ ......

    Graphically:

  ---

  ---

  ---

  ---

• The Self-Clocked Fair Queueing (SCFQ) Method
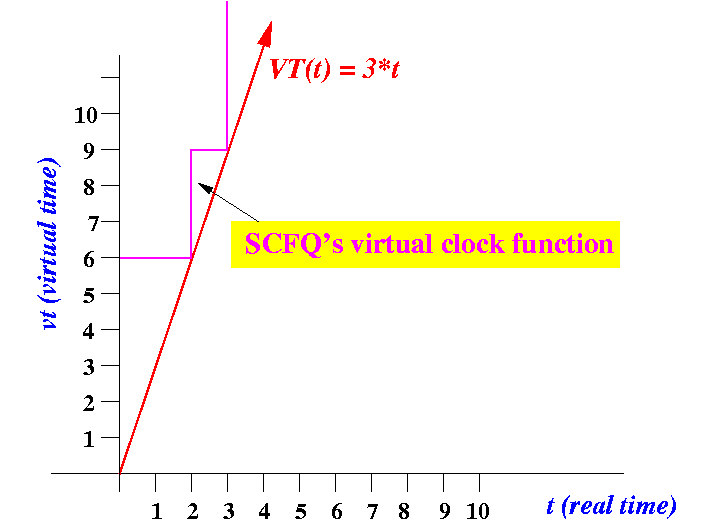
  • Information maintained by SCFQ:

    V(pji) = the time stamp assigned to the last arriving packet pji of flow j           (V(pj0) = 0) VT(t) = the virtual time (clock) at time t (real time)

    ---

  • When the next packet p_jⁱ⁺¹ of flow j arrives:

    Let A(pji+1) = time (real time) that packet pji+1 arrives Let len(pji+1) = length (#bytes) of the packet pji+1 ---- \ 1 S(t) = > --- / wf ---- All active flows f at time real time t 1. Assign time stamp to packet pji+1 len(pji+1) V(pji+1) = max ( VT(A(pji+1)), V(pji) ) + ----------- S(A(pji+1) 2. Enter pji+1 into the SCFQ queue ordered by the value of the time stamps V(pji+1)

    ---

  • When a packet p finishes transmission:

    Let V(p) = time stamp of the packet p 1. Set virtual time (clock) VT = V(p) 2. Transmit the next packet in the packet queue

  ---

  ---

  ---

  ---

  ---

  ---

• Timing difference between WFQ and SCFQ - by example
  • The following example shows the difference in assigning time stamps to packets in WFQ and SCFQ

    3 flows: w1 = 1/3 w2 = 1/3 w3 = 1/3            Packet arrivals: (3 packets from flow 1)             t = 0, len(p11) = 2 t = 1, len(p21) = 1            Virtual packet lengths: virtual len(p11) = 6 virtual len(p21) = 3

    ---

  • The packets are assigned time stamps as follows in WFQ:

    Time stamps assigned in WFQ: p11 arrives, receives V(p11) = 6 ^ p12 arrives, receives V(p11) = 3 + 3 = 6 | ^ | | | | |--------+--------+--------+--------+--------+--------+------------> real time t=0 t=1 t=2 t=3 t=4 t=5 t=6 vt=0 vt=3 |--------+ vt=3t

    Because: VT(3) = 3

    ---

  • The packets are assigned time stamps as follows in SCFQ:

    Time stamps assigned in WFQ: p11 arrives, receives V(p11) = 6 ^ p12 arrives, receives V(p11) = 6 + 3 = 9 | ^ | | | | |--------+--------+--------+--------+--------+--------+------------> real time t=0 t=1 t=2 t=3 t=4 t=5 t=6 vt=6 vt=6 |-----------------+ <----- vt=6 ----->

    Because: VT(3) = 6 !!!

  ---

  ---

• Scheduling in SCFQ: Example 1
  • Flows: flow 1 and flow 2

  • Weight assignments:
    • w₁ = 0.5
    • w₂ = 0.5

  • Packet arrival:

    Flow 1: FLow 2: Arrival Time Packet length Arrival Time Packet length Packet 1: 1 1 0 3 Packet 2: 2 1 5 2 Packet 3: 3 2 9 2 Packet 4: 11 2 - -

    ---

  • Worked out example:

    Initialization: t = 0 vt = 0 SCFQ server ---------- Last time stamp(Flow 1): 0 Last time stamp(Flow 2): 0 PacketQ: Event 1: t = 0 p21 arrives t = 0 vt = 0 / V(p21) = max(0,0) + 3/(0.5) = 6 SCFQ server ---------- Last time stamp(Flow 1): 0 Last time stamp(Flow 2): 6 PacketQ: (6)p21[len=3] \ t = 0 vt = 6 ==================================== Next arrival time = 1 sec later Next departure time = 3 sec later ===================================== Event 2: t = 1 p11 arrives t = 1 vt = 6 / V(p11) = max(6,0) + 1/(0.5) = 8 SCFQ server ---------- Last time stamp(Flow 1): 8 Last time stamp(Flow 2): 6 PacketQ: (6)p21[len=2] (8)p11[len=1] \ t = 1 vt = 6 ==================================== Next arrival time = 1 sec later Next departure time = 2 sec later ===================================== Event 3: t = 2 p12 arrives t = 1 vt = 6 / V(p12) = max(6,8) + 1/(0.5) = 10 SCFQ server ---------- Last time stamp(Flow 1): 10 Last time stamp(Flow 2): 6 PacketQ: (6)p21[len=1] (8)p11[len=1] (10)p12[len=1] \ t = 2 vt = 6 ==================================== Next arrival time = 1 sec later Next departure time = 1 sec later ===================================== Event 4: t = 3 p13 arrives t = 3 vt = 6 / V(p13) = max(6,10) + 2/(0.5) = 14 SCFQ server ---------- Last time stamp(Flow 1): 14 Last time stamp(Flow 2): 6 PacketQ: (6)p21[len=0] (8)p11[len=1] (10)p12[len=1] (14)p13[len=2] \ t = 3 vt = 6 ==================================== Next arrival time = 2 sec later Next departure time = 0 sec later ===================================== Event 5: t = 3 p21 departs t = 3 vt = 6 SCFQ server ---------- Last time stamp(Flow 1): 14 Last time stamp(Flow 2): 6 PacketQ: (8)p11[len=1] (10)p12[len=1] (14)p13[len=2] \ t = 3 vt = 8 *** Virtual clock advances ! ==================================== Next arrival time = 2 sec later Next departure time = 1 sec later ===================================== Event 6: t = 4 p11 departs t = 4 vt = 8 SCFQ server ---------- Last time stamp(Flow 1): 14 Last time stamp(Flow 2): 6 PacketQ: (10)p12[len=1] (14)p13[len=2] \ t = 4 vt = 10 *** Virtual clock advances !!! ==================================== Next arrival time = 1 sec later Next departure time = 1 sec later ===================================== Event 7: t = 5 p22 arrives t = 5 vt = 10 / V(p22) = max(10,6) + 2/(0.5) = 14 SCFQ server ---------- Last time stamp(Flow 1): 14 Last time stamp(Flow 2): 14 PacketQ: (10)p12[len=0] (14)p13[len=2] (14)p22[len=2] \ t = 5 vt = 10 ==================================== Next arrival time = 4 sec later Next departure time = 0 sec later ===================================== Event 8: t = 5 p12 departs t = 5 vt = 10 SCFQ server ---------- Last time stamp(Flow 1): 14 Last time stamp(Flow 2): 14 PacketQ: (14)p13[len=2] (14)p22[len=2] \ t = 5 vt = 14 *** Virtual clock advances !!! ==================================== Next arrival time = 4 sec later Next departure time = 2 sec later ===================================== Event 9: t = 7 p13 departs t = 7 vt = 14 SCFQ server ---------- Last time stamp(Flow 1): 14 Last time stamp(Flow 2): 14 PacketQ: (14)p22[len=2] \ t = 7 vt = 14 *** Virtual clock can remain unchanged !!! ==================================== Next arrival time = 2 sec later Next departure time = 2 sec later ===================================== Event 10: t = 9 p23 arrives t = 9 vt = 14 / V(p23) = max(14,14) + 2/(0.5) = 18 SCFQ server ---------- Last time stamp(Flow 1): 14 Last time stamp(Flow 2): 18 PacketQ: (14)p22[len=0] (18)p23[len=2] \ t = 9 vt = 14 ==================================== Next arrival time = 2 sec later Next departure time = 0 sec later ===================================== Event 11: t = 9 p22 departs t = 9 vt = 14 SCFQ server ---------- Last time stamp(Flow 1): 14 Last time stamp(Flow 2): 18 PacketQ: (18)p23[len=2] \ t = 9 vt = 18 ==================================== Next arrival time = 2 sec later Next departure time = 2 sec later ===================================== Event 12: t = 11 p14 arrives t = 11 vt = 18 / V(p23) = max(18,14) + 2/(0.5) = 22 SCFQ server ---------- Last time stamp(Flow 1): 22 Last time stamp(Flow 2): 18 PacketQ: (18)p23[len=0] (22)p14[len=2] \ t = 11 vt = 18 ==================================== Next arrival time = - Next departure time = 0 sec later ===================================== Event 13: t = 11 p23 departs t = 11 vt = 18 SCFQ server ---------- Last time stamp(Flow 1): 22 Last time stamp(Flow 2): 18 PacketQ: (22)p14[len=2] \ t = 11 vt = 22 ==================================== Next arrival time = - Next departure time = 2 sec later ===================================== Event 13: t = 13 p14 departs t = 13 vt = 22 SCFQ server ---------- Last time stamp(Flow 1): 22 Last time stamp(Flow 2): 18 PacketQ: ---

  ---

  ---

• Scheduling in SCFQ: Example 2 (for your eyes only)
  • Flows: flow 1 and flow 2

  • Weight assignments:
    • w₁ = 1/3
    • w₂ = 2/3

  • Packet arrival:

    Flow 1: FLow 2: Arrival Time Packet length Arrival Time Packet length Packet 1: 1 1 0 3 Packet 2: 2 1 5 2 Packet 3: 3 2 9 2 Packet 4: 11 2 - -

    ---

  • SCFQ Work Sheet:

    When an arrival and a departure happens "at the same time", assume that the arrival happens first

    Real Time	Virt Time	Arrival	Departure	Max TS flow1	Max TS flow2	Queued Packets	Packet Transmitted
    0	0	---	---	0	0	---	---
    0	0	Flow2,Pkt1, len=3,TS=4.5	---	0	4.5	Flow2,Pkt1(TS=4.5)	---
    0+	4.5	---	---	0	4.5	Flow2,Pkt1(TS=4.5)	Flow2,Pkt1(Fin=3)
    1	4.5	Flow1,Pkt1, len=1,TS=7.5	---	7.5	4.5	Flow2,Pkt1(TS=4.5) Flow1,Pkt1(TS=7.5)	Flow2,Pkt1(Fin=3)
    2	4.5	Flow1,Pkt2, len=1,TS=10.5	---	10.5	4.5	Flow2,Pkt1(TS=4.5) Flow1,Pkt1(TS=7.5) Flow1,Pkt2(TS=10.5)	Flow2,Pkt1(Fin=3)
    3-	4.5	Flow1,Pkt3, len=2,TS=16.5	---	16.5	4.5	Flow2,Pkt1(TS=4.5) Flow1,Pkt1(TS=7.5) Flow1,Pkt2(TS=10.5) Flow1,Pkt3(TS=16.5)	Flow2,Pkt1(Fin=3)
    3	4.5	---	Flow2,Pkt1(TS=4.5)	16.5	4.5	Flow1,Pkt1(TS=7.5) Flow1,Pkt2(TS=10.5) Flow1,Pkt3(TS=16.5)	---
    3+	7.5(!!)	---	---	16.5	4.5	Flow1,Pkt1(TS=7.5) Flow1,Pkt2(TS=10.5) Flow1,Pkt3(TS=16.5)	Flow1,Pkt1(Fin=4)
    4	7.5	---	Flow1,Pkt1(TS=7.5)	16.5	4.5	Flow1,Pkt2(TS=10.5) Flow1,Pkt3(TS=16.5)	---
    4+	10.5(!!)	---	---	16.5	4.5	Flow1,Pkt2(TS=10.5) Flow1,Pkt3(TS=16.5)	Flow1,Pkt2(Fin=5)
    5-	10.5	Flow2,Pkt2, len=2,TS=13.5**	---	16.5	13.5	Flow1,Pkt2(TS=10.5) Flow2,Pkt2(TS=13.5) Flow1,Pkt3(TS=16.5)	Flow1,Pkt2(Fin=5)
    5	10.5	---	Flow1,Pkt2(TS=10.5)	16.5	13.5	Flow2,Pkt2(TS=13.5) Flow1,Pkt3(TS=16.5)	---
    5+	13.5(!!)	---	---	16.5	13.5	Flow2,Pkt2(TS=13.5) Flow1,Pkt3(TS=16.5)	Flow2,Pkt2(Fin=7)
    7	13.5	---	Flow2,Pkt2(TS=13.5)	16.5	13.5	Flow1,Pkt3(TS=16.5)	---
    7+	16.5(!!)	---	---	16.5	13.5	Flow1,Pkt3(TS=16.5)	Flow1,Pkt3(Fin=9)
    9-	16.5	Flow2,Pkt3, len=2,TS=19.5	---	16.5	19.5	Flow1,Pkt3(TS=16.5) Flow2,Pkt3(TS=19.5)	Flow1,Pkt3(Fin=9)
    9	16.5	---	Flow1,Pkt3(TS=16.5)	16.5	19.5	Flow2,Pkt3(TS=19.5)	---
    9+	19.5(!!)	---	---	16.5	19.5	Flow2,Pkt3(TS=19.5)	Flow2,Pkt3(Fin=11)
    11-	19.5	Flow1,Pkt4, len=2,TS=25.5	---	25.5	19.5	Flow2,Pkt3(TS=18) Flow1,Pkt4,(TS=25.5)	Flow2,Pkt3(Fin=11)
    11	19.5	---	Flow2,Pkt3(TS=19.5)	25.5	19.5	Flow1,Pkt4,(TS=25.5)	---
    11+	25.5	---	---	25.5	19.5	Flow1,Pkt4,(TS=25.5)	Flow1,Pkt4,(Fin=13)
    13	25.5	---	Flow1,Pkt4,(Fin=13)	25.5	19.5	---	---

    Notes:

    Notice again that whenever a new packet is scheduled for transmission , the virtual time is updated - the virtual time is set equal to the time stamp of the newly scheduled packet !! ** The time stamp assigned to Packet 2 of flow 2 is: TS = max(4.5, 10.5) + 2/(0.66666...) = 10.5 + 3 = 13.5

  ---

  ---

• Maximum Lag Time in SCFQ
  • Maximum lag time in SCFQ:

    In other words:

    Departure time of packet p from flow k in FFS | | max. packet size | lag time ≤ -------------------- | rk V <---------------------------------->| -------------+--------------------------------------------- |<--------------------------------------------->| Possible departure times of packet p in SCFQ

    (If a packet depart before its departure time in FFS, there is no lag time)

    ---

  • Conclusion:

    The SCFQ method is less fair that the best possible fair WFQ method

    So what did we gain ?

  ---

  ---

  ---

  ---

• Running Time complexity of SCFQ

  • Advantage of SCFQ over WFQ:

    SCFQ has a running time of log(n) - where n = number of packets in the queue

  • This is because SCFQ must insert a new packet into the queue in ascending order of time stamps.

    To find the place of insertion, SCFQ must do a binary search which has running time log(n) in the number of packets in the queue)