- TCP Reno throughput:
E[n] * E[Y] + E[R] TCP Throughput = ----------------------- (See: click here) E[n] * E[A] + E[Z]With:
---------------------- / 1-p 2+b / 8(1-p) 2+b 2 E[Y] = ----- + ----- + \ / -------- + ( ----- ) . . . . . . . . (5) p 3b \/ 3bp 3b
-- ------------------------- --- | 2+b / 2 b (1-p) 2+b 2 | E[A] = RTT * | --- + \ / ----------- + ( ----- ) + 1 | . . . (6) | 6 \/ 3p 6 | -- ---
- In the previous webpage,
we have computed (estimated)
E[n]
- In this webpage, we will derive expressions for E[R] and E[A].
- In order to compute:
- E[R] = average number of packets in the retransmissions in one Reno cycle
We must first determine:
- Number of packets in the retransmissions in one Reno cycle
Graphically:
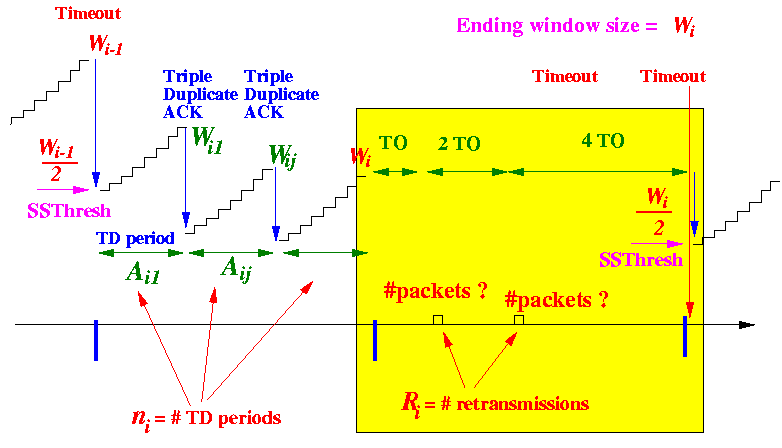
The only way to know how many packets are transmitted in one TO period is by observation :-)
- Empiral result:
- Padhye found empirically that in most cases , one packet is transmitted between 2 consecutive timeout events
- In other words:
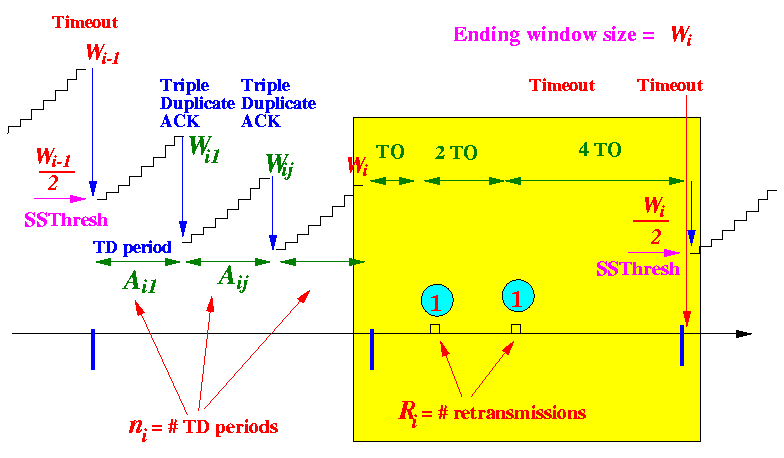
- In general:
E[R] = h1 * Prob[R=1] + h2 * Prob[R=2] + h3 * Prob[R=3] + ... = h * Prob[R=1] + 2 * h * Prob[R=2] + 3 * h * Prob[R=3] + ... where: R = number of retransmissions h = number of packets transmitted in one round of retransmission
- From Padhye's empirical observation:
E[R] = 1 * Prob[R=1] + 2 * 1 * Prob[R=2] + 3 * 1 * Prob[R=3] + ... = 1 * Prob[R=1] + 2 * Prob[R=2] + 3 * Prob[R=3] + ...
- P[R = k]:
Prob[ R = k ] = probability that there are k retransmission rounds = Prob[ (k - 1 transmissions end in TO) AND last transmission success ]There is one packet in a retransmission round !!!
Summary: Prob[ R = k ] = pk-1 * (1 - p)
- E[R] :
E[R] = 1*Prob[R=1] + 2*Prob[R=2] + 3*Prob[R=3] + ... = 1 * (1-p) + 2 * p*(1-p) + 3 * p2*(1-p) + ....
Using Maple: > sum( k * p^(k-1) * (1-p), k=0..infinity); Does not converge - Maple needs more information on p: > assume(p>0, p<1); > sum( k * p^(k-1) * (1-p), k=0..infinity); 1 - ------ p~ - 1 1 = ------- 1 - p
Conclussion: 1 1 E[R] = -------- = ------- . . . . . . . . . . . . . . (1) -1 + p 1 - p
- Let
TO
denote the base timeout value
used by the TCP connection
Note: the base timeout value if set to:
- TO = 4 * RTT
- Each time when TCP
timeout ,
the timeout value is
doubled
........ but the doubling occurs upto 6 (SIX) times.
- The timeout value
used in each timeout:
# Times TCP times out | Timeout value used | Start to end of Timeout ------------------------+---------------------+---------------------------- Initial timeout | TO | TO 2nd timeout | 2*TO | 3*TO 3rd timeout | 4*TO | 7*TO 4th timeout | 8*TO | 15*TO 5th timeout | 16*TO | 31*TO 6th timeout | 32*TO | 63*TO 7th timeout | 64*TO | (63+64)*TO 8th timeout | 64*TO | (63+2*64)*TO 9th timeout | 64*TO | (63+3*64)*TO ...Notes:
- Initially, the
timeout value is set to
TO
- When the retransmitted packet
times out,
the retransmission will use a
timeout value of
2*TO
- When the retransmitted packet
times out agaion,
the retransmission will use a
timeout value of
4*TO
- And so on.
Until the timeout value reaches 64*TO .
When it reaches 64*TO, the timeout value is not increased further.
- Initially, the
timeout value is set to
TO
- E[Z]:
E[Z] = L1 * Prob[R=1] + L2 * Prob[R=2] + L3 * Prob[R=3] + ...
Li = length of the timeout period if R = i
Or: E[Z] = TO (1-p) * { p0 + p1 * (3) + p2 * (7) + p3 * (15) + p4 * (31) + p5 * (63) + p6 * (63+1*64) + p7 * (63+2*64) + p8 * (63+3*64) + .... }
- We call in the help of Maple to compute the sum:
> assume( p>=0, p<1 ); > h1 := p^0 + 3*p^1 + 7*p^2 + 15*p^3 + 31*p^4 + 63*p^5 \ + sum( (63+(k-5))*p^k, k=6..infinity); 6 2 3 4 5 p~ (63 p~ - 64) h1 := 1 + 3 p~ + 7 p~ + 15 p~ + 31 p~ + 63 p~ - ---------------- 2 (p~ - 1)
> % * (1-p); / 6 \ | 2 3 4 5 p~ (63 p~ - 64)| |1 + 3 p~ + 7 p~ + 15 p~ + 31 p~ + 63 p~ - ----------------| (1 - p~) | 2 | \ (p~ - 1) / > simplify(%); 2 3 4 5 6 -2 p~ - p~ - 1 - 4 p~ - 8 p~ - 16 p~ + 31 p~ ------------------------------------------------- p~ - 1
Therefore: 2 3 4 5 6 1 + p +2 p + 4 p + 8 p + 16 p - 31 p E[Z] = TO ------------------------------------------ . . . . . . (2) 1 - p (Looks like there is a typo in the paper, Padhye has "+ 32 p6")
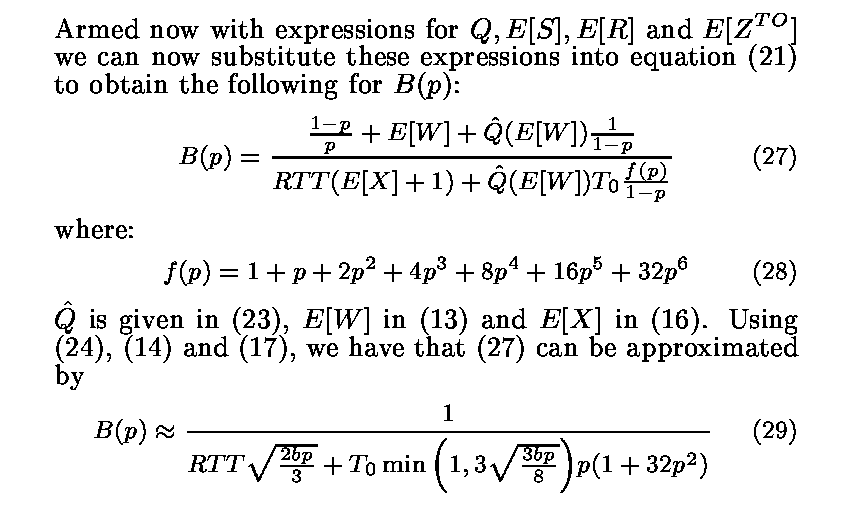
|