---

Introduction to queueing theory

---

---

• Queue
  • A queue is a waiting line...

  • The behaviour of a queue is characterized by following parameters:

    the arrival process (commonly used: Poisson process) the service (departure) process (commonly used: Poisson process) the number of servers in the system The queueing discipline (often FIFO) The capacity of the queue (buffer space) The size of the client population (commonly used value: infinite)

  ---

  ---

• Kendall notation for a queueing system
  • Kendall's notation (or sometimes Kendall notation) the standard system used to describe and classify the queueing model that a queueing system corresponds to.

    The notation was first suggested by D. G. Kendall in 1953

    ---

  • Long Kendall notation:

    A | B | c | D | E | F ^ ^ ^ ^ ^ ^ | | | | | | | | | | | +--- queueing discipline (default: FIFO) | | | | +--- population size (default: infinite) | | | +--- queue capacity (default: infinite) | | +--- number of servers | +--- server process +--- arrival process

    Abbreviated Kendall notation:

    A | B | c ^ ^ ^ ^ ^ ^ | | | | | | | | | | | +--- queueing discipline is FIFO | | | | +--- population size is infinite | | | +--- queue capacity is infinite | | +--- number of servers | +--- server process +--- arrival process

    ---

  • Further notations:

    Abreviations for arrival and service processes: M = Poisson process D = Deterministic process (fixed time between 2 consecutive events) G = general process

  ---

  ---

• The classic M/M/1 queue
  • The M/M/1 queue is a short hand notation for the M/M/1/∞/∞/FIFO queue:

    M = arrival process is Poisson (with some parameter lambda;) M = service (departure) process is Poisson (with some parameter lambda;) 1 = there is 1 server in system ∞ = infinite queue capacity; no arriving client will be rejected ∞ = infinite population size (the arrival process will be unaffected by the number of clients already in the system) FIFO = first in first out service

    ---

  • The rate transition diagram for the M/M/1 queueing system is:

    We have already studied this system...

  ---

  ---

  ---

  ---

• One more servers: the M/M/2 system
  • The rate transition diagram for the M/M/2 system is:

    ---

  • Equilibrium equations for M/M/2:

    p0 × λ = p1 × μ p1 × λ = p2 × 2μ p2 × λ = p3 × 2μ p3 × λ = p4 × 2μ ....

  ---

  ---

• More servers in general: M/M/k
  • The rate transition diagram for the M/M/k system is:

    ---

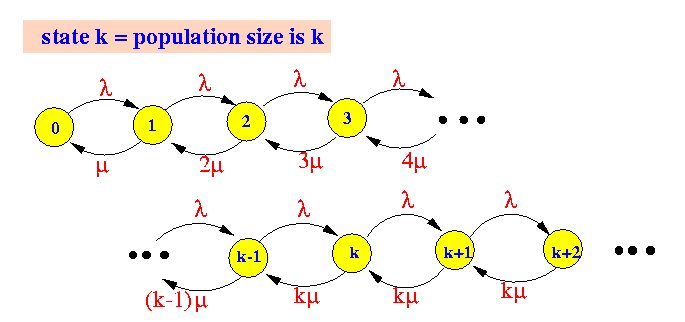
  • Equilibrium equations for M/M/k:

    p0 × λ = p1 × μ p1 × λ = p2 × 2μ p2 × λ = p3 × 3μ .... pk-2 × λ = pk-1 × (k-1)μ pk-1 × λ = pk × kμ pk × λ = pk+1 × kμ pk+1 × λ = pk+2 × kμ pk+2 × λ = pk+3 × kμ ....

  ---

  ---

  ---

  ---

• Finite buffer capacity: M/M/1/k
  • The M/M/1/k queue is a short hand notation for the M/M/1/k/∞/FIFO queue:

    M = arrival process is Poisson (with some parameter lambda;) M = service (departure) process is Poisson (with some parameter lambda;) 1 = there is 1 server in system k = queue capacity; the (k+1)th arriving client will be rejected ∞ = infinite population size (the arrival process will be unaffected by the number of clients already in the system) FIFO = first in first out service

    ---

  • The rate transition diagram for the M/M/1/k queueing system is:

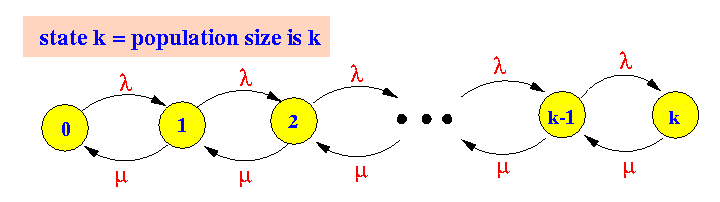
    Notice that:

    The number of customers in the system is at most k Hence, the states of this Markov chain are 0, 1, 2, ..., k

    ---

  • Equilibrium equations for M/M/1/k:

    p0 × λ = p1 × μ p1 × λ = p2 × μ p2 × λ = p3 × μ p3 × λ = p4 × μ .... pk-1 × λ = pk × μ