Performance Analysis of the unslotted 1-persistent CSMA protocol

Some observations about the 1-persistent CSMA protocol

A quick refresher of the 1-persistent CSMA protocol:

Fact of the 1-persistent CSMA protocol:

When a node senses that the channel is busy, it will wait for the end of the transmission and transmit immediately
Consequence of this fact:

All nodes that sense the channel is busy (during some node's transmission) will transmit their packets at the end of the current transmission

Transmission pattern in the 1-persistent CSMA protocol:

When observing the 1-persistent CSMA protocol, you will see the following transmission pattern:

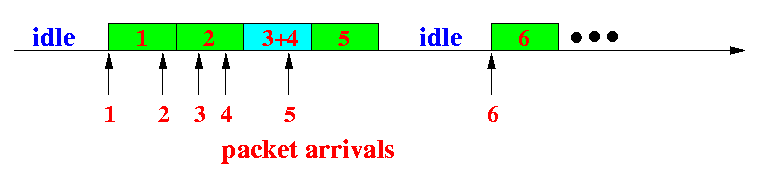
Notes:

There are again a series of interleaved busy periods and idle periods
Each cyle starts with an idle period, followed by a busy period
A busy period in the 1-persistent CSMA protocol consists of one or more transmission periods
(A busy period in the non-persistent CSMA protocol consists of exactly one transmission period
This is because when a node senses that the channel is busy in the non-persistent CSMA protocol, it will leave the queueing system)

Anatomy of the 1-persistent CSMA busy period:

The transmission periods inside one busy period can be of the following type:

Notes:

There are two different types of transmission periods inside a busy period

The first type is a transmission period where the number of packet arrivals at the start of the transmission period is equal to 1

We call this a type 1 period

Type 1 periods can become useful

A type 1 period can contain a collision when another packet arrives during the vulnerable period:

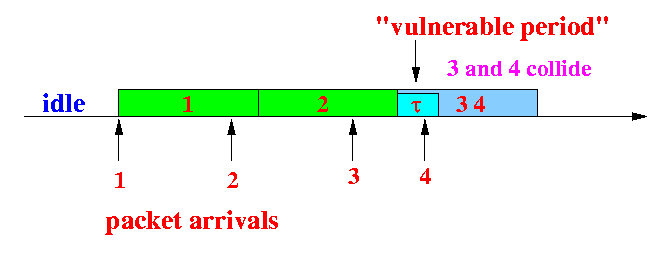
Note:

All three periods in the figure are type 1 periods
(There is only one packet arrival at the start of the period
The period #1 and #2 are useful periods because the packet arrival will not cause a collision
The period #3 is notuseful because the arrival of packet 4 will cause a collision
The first transmission period in a busy period is always a type 1 period
(Because there are no simultaneous arrivals in a Poisson Arrival process)

The other type is a transmission period contains a transmission of 2 or more packets
Example:
The period #3 (with cyan color) is a type 2 period
Type 2 periods are certainly not useful
(because there will be a collision in the transmission period)

According to the same principle (counting the number of arrivals in the previous transmission period), we see that:
We will use a similar nomenclature for the idle period:

Markov transistion diagram for the 1-persistent CSMA protocol

Definitions of the different states:

State 0 = the number of packet arrivals at the start of the transmission period is equal to 0
State 1 = the number of arrivals at the start of the transmission period is equal to 1
State 2 = the number of arrivals at the start of the transmission period is equal to 2

The state transition diagram of the 1-persistent (unslotted) CSMA protocol:
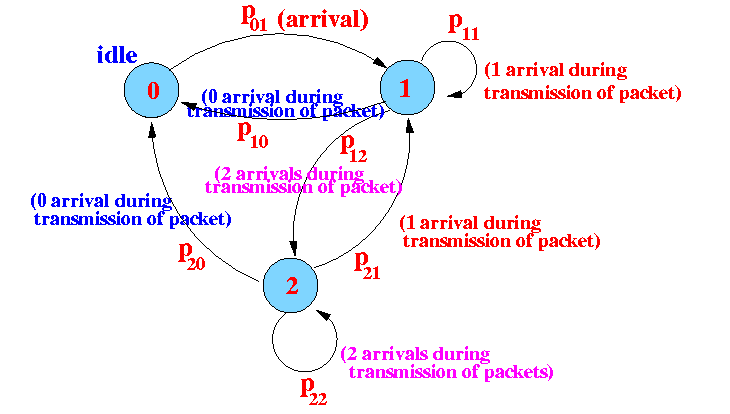
Example state transitions:

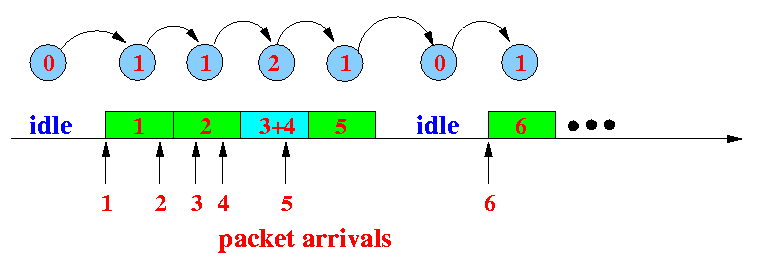
Throughtput of the unslotted 1-persistent CSMA protocol

Definitions and notations:

π_i = steady state probability of the system in state i (for i = 0, 1, 2)
T_i = random variable representing the length (duration) of a type i period (for i = 0, 1, 2)
T_i = E[T] (i.e., the average length (duration) of a type i period (for i = 0, 1, 2)

Note:

Do not confuse the random variable T_i with the constant T
Recall that:

Throughput of the unslotted 1-persistent CSMA protocol:

π₀T × Ҏ[ success in T₀ ] + π₁T × Ҏ[ success in T₁ ] + π₂T × Ҏ[ success in T₂ ] S = --------------------------------------------------------------------------------- π₀T₀ + π₁T₁ + π₂T₂ π₀T × 0 + π₁T × Ҏ[ 0 arrival in τ sec ] + π₂T × 0 <=> S = ---------------------------------------------------------- π₀T₀ + π₁T₁ + π₂T₂ π₁T × e^-gτ <=> S = --------------------- .......... (1) π₀T₀ + π₁T₁ + π₂T₂

Notes:

The expression:

π_iT_i + π₁T₁ + π₂T₂

in the denominator is the average duration (length) of one transmission period

Example:

Suppose 40% of the time, the system is in state 0 that last approximately 5 min, 50% of the time, the system is in state 1 that last approximately 1 min, and 10% of the time, the system is in state 2 that last approximately 2 min, then the average duration of one period is:

The expression:
in the nominator is the portion of the duration "π_iT_i" that is useful (successful packet transmission

What remains to be done:

T₀: The average length of a type 0 period

The type 0 period is an idle period
Hence:

The duration of an idle period depends only on the arrival process

Since the arrival process is a Poisson process with arrival rate g, the duration of an idle period in 1-persistent CSMA is the same as the duration of an idle period in non-persistent CSMA

Therefore:

1 T₀ = --- ........ (2) (See: click here) g

T₁: The average length of a type 1 period

Note:

Although there is one arrival at the start of a type 1 period, it is not true that a type 1 period will always contain one packet transmission
The number of packets transmitted in a type 1 period depends on the number of arrivals during the vulnerable period of the initiating transmission

Anatomy of a type 1 transmission period:
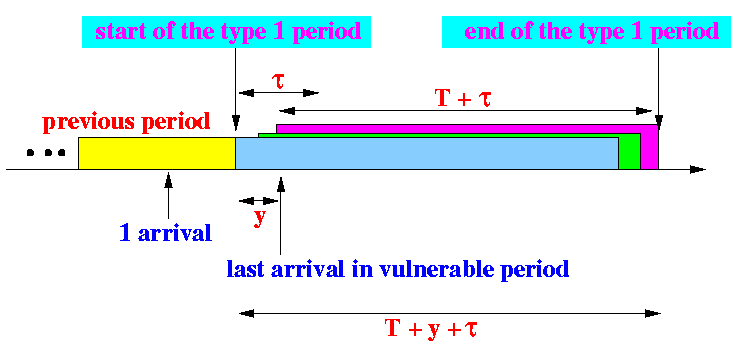
Notes:
We have that:
(For detail on why you have &tau in the expression, see: click here)
Therefore:
The random variable y (arrival time of the last arriving packet) depends only on the arrival process
For a Poisson arrival process with arrival rate g, we have previously determined that (see: click here)

Therefore, the average duration of a type 1 period is:

E[T₁] = T + τ + E[y]
Or: 1 - e^-gτ T₁ = T + 2τ - --------- ...... (4) g

T₂: The average length of a type 2 period

Note:

Similar to the type 1 period:
The number of packets transmitted in a type 2 period also depends on the number of arrivals during the vulnerable period of the initiating transmissions

Anatomy of a type 2 transmission period:
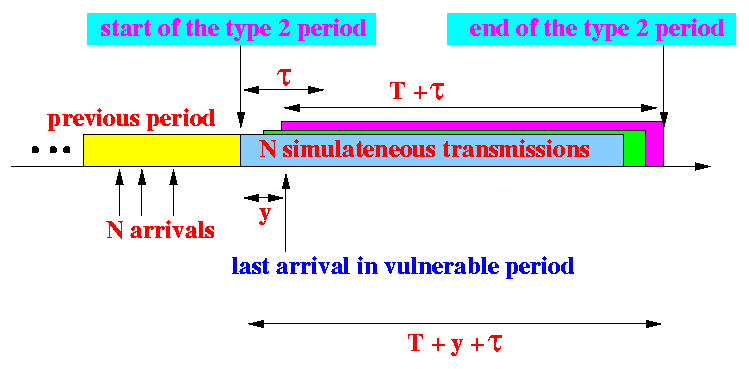
Notes:
We see that:

Therefore:

E[T₂] = E[T₁]
Or: 1 - e^-gτ T₂ = T + 2τ - --------- ...... (5) g

OK, we got expressions for T₀, T₁ and T₂....
Now we find the steady state probabilities π₀, π₁ and π₂....

Steady state probability π₀, π₁ and π₂

Here we apply the material from Markov chain....
(We get to finally use this !!! :-))

However, before we can apply the Markov analysis, we must first determine the transistion probabilities p₀₀, p₀₁, p₀₂, p₁₀, ...

Unlike artificially created Markov chains with chosen transition probabilities (such as those in your homework assignment), real-life systems have transition probabilities that must be discovered by analysis

Consider the state transition diagram:

The steady state probabilities π₀, π₁, π₂ are computed using the following equations: (See: click here)

π₀ = π₀p₀₀ + π₁p₁₀ + π₂p₂₀ π₁ = π₀p₀₁ + π₁p₁₁ + π₂p₂₁ π₂ = π₀p₀₂ + π₁p₁₂ + π₂p₂₂
From the diagram, we have: p₀₀ = 0 and p₀₂ = 0 Subst: p₀₀ = 0 and p₀₂ = 0 in the equations: π₀ = π₁p₁₀ + π₂p₂₀ π₁ = π₀p₀₁ + π₁p₁₁ + π₂p₂₁ π₂ = π₁p₁₂ + π₂p₂₂
From: p₀₀ + p₀₁ + p₀₂= 1 and: p₀₀ = 0 and: p₀₂ = 0 We have: p₀₁ = 1 Substitute p₀₁ = 1: π₀ = π₁p₁₀ + π₂p₂₀ π₁ = π₀ + π₁p₁₁ + π₂p₂₁ π₂ = π₁p₁₂ + π₂p₂₂

Further simplification:

The transition probability from state 1 to state 0 (p₁₀) depends on the number of arrivals in a type 1 period
(Specifically: state 0 is reached when there are no arrivals within the type 1 period)
The transition probability from state 2 to state 0 (p₂₀) also depends on the number of arrivals in a type 2 period
(Specifically: state 0 is reached when there are no arrivals within the type 2 period)

Recall that:
Because the arrival process to type 1 and type 2 periods are also identical (Poisson with rate g), we conclude that:
The transition probability from state 1 to state 1 (p₁₁) depends on the number of arrivals in a type 1 period
(Specifically: state 1 is reached when there are exactly 1 arrival within the type 1 period)
The transition probability from state 2 to state 1 (p₂₁) also depends on the number of arrivals in a type 2 period
(Specifically: state 1 is reached when there are exactly 1 arrival within the type 2 period)

Recall again that:
Because the arrival process to type 1 and type 2 periods are also identical (Poisson with rate g), we conclude that:
The transition probability from state 1 to state 2 (p₁₀) depends on the number of arrivals in a type 1 period
(Specifically: state 2 is reached when there are more than 2 arrivals within the type 1 period)
The transition probability from state 2 to state 0 (p₂₀) also depends on the number of arrivals in a type 2 period
(Specifically: state 2 is reached when there are more than 2 arrivals within the type 2 period)

Same old story again, recall that:
Because the arrival process to type 1 and type 2 periods are also identical (Poisson with rate g), we conclude that:

Result after substitution:

Before substitution: π₀ = π₁p₁₀ + π₂p₂₀ π₁ = π₀ + π₁p₁₁ + π₂p₂₁ π₂ = π₁p₁₂ + π₂p₂₂
Before substitution: π₀ = π₁p₁₀ + π₂p₁₀ π₁ = π₀ + π₁p₁₁ + π₂p₁₁ π₂ = π₁p₁₂ + π₂p₁₂

Recall that the system of equilibrium equations is singular and we must replace any one of the equations with: π₀ + π₁ + π₂ = 1 (See: click here)

Result:

π₀ = π₁p₁₀ + π₂p₁₀ ~~π₁ = π₀ + π₁p₁₁ + π₂p₁₁~~ ====> π₀ + π₁ + π₂ = 1 π₂ = π₁p₁₂ + π₂p₁₂
π₀ = π₁p₁₀ + π₂p₁₀ π₂ = π₁p₁₂ + π₂p₁₂ π₀ + π₁ + π₂ = 1

Solving π₀, π₁, π₂ (with Maple):

> eq1 := q0 = p10*q1 + p10*q2; eq1 := q0 = p10 q1 + p10 q2 > eq2 := q2 = p12*q1 + p12*q2; eq2 := q2 = p12 q1 + p12 q2 > eq3 := q0 + q1 + q2 = 1; eq3 := q0 + q1 + q2 = 1 > solve( { eq1, eq2, eq3 }, {q0, q1, q2} ); p12 -1 + p12 p10 {q2 = -------, q1 = - --------, q0 = -------} 1 + p10 1 + p10 1 + p10

Note that:

p₁₀ + p₁₁ + p₁₂ = 1 (this is the sum of all "exit" probabilities from state 1)

Therefore, we can rewrite the solution as:

p₁₀ π₀ = --------- ........ (6) 1 + p₁₀ p₁₀ + p₁₁ π₁ = ----------- ........ (7) 1 + p₁₀ 1 - p₁₀ - p₁₁ π₂ = -------------- ........ (8) 1 + p₁₀

Now all we still need to do is compute p₁₀ and p₁₁ :-)

Computing the transition probability p₁₀

Transition from state 1 to state 0:

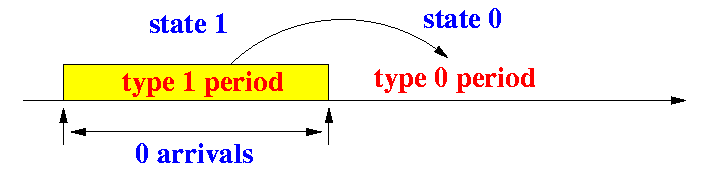
Note:

The system moves from state 1 to state 0 (idle) when there are 0 arrivals within the type 1 period
The number of arrivals in the type 1 period depends on the duration (length) of the type 1 period

To obtain the duration of the type 1 period, we must look at the anatomy of a type 1 transmission period:

Suppose a type 1 period is started at time t by the packet transmission x:

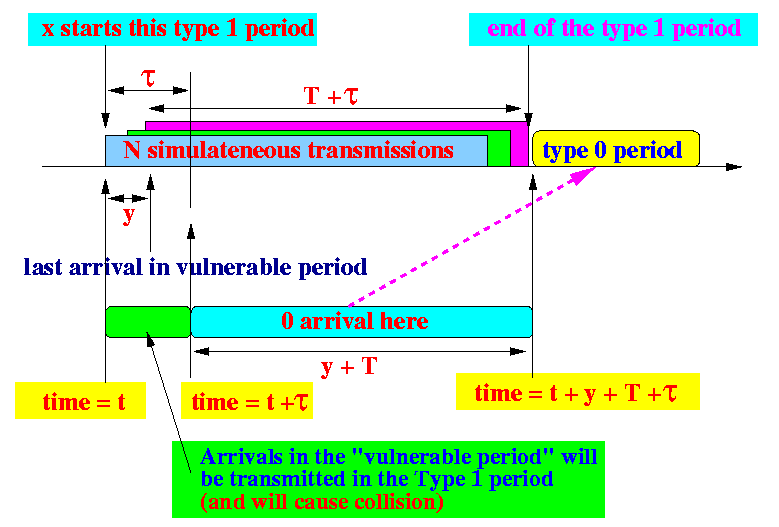
Observation 1:

Arrivals that arrive before time t + τ will not detect the starting transmission x
Consequently, they will schedule themselves for transmission within the type 1 period (and they will cause a collision)
Arrivals that arrive after time t + τ will detect the starting transmission x
Consequently, they will schedule themselves for transmission after the type 1 period

Observation 2:

The total length of the type 1 period is T + τ + y
(y is the time of the last arriving packet before deadline τ)
In order to transit to a type 0 (idle) period, there must be zero (0) arrivals between: [t + τ, t + y + T + τ)
I.e., there must be zero (0) arrivals in (T + y) sec

Thus: the probability that a state 1 period will transits into a type 0 period is equal to:

p₁₀ = Ҏ[ 0 arrivals in (T + y) sec ]

If y were a constant, the solution would be simple:

(g(T + y))⁰ ---------- e^{-g(T + y)} (Poisson arrivals) 0!

BUT, y is a random variable

The technique used to compute Ҏ[ 0 arrivals in (T + y) sec ] is the Law of Total Probability (see: click here):

(We divide the range "[0, τ]" into individual time instances u)

p₁₀ = ∑^τ_u=0 Ҏ[ 0 arrivals in T + y | y = u ] × Ҏ[ y = u ] (Law of Tatal Probability) = ∑^τ_u=0 Ҏ[ 0 arrivals in T + u ] × Ҏ[ y = u ]
The sum is in fact an integral because the random variable y is a continuous random variable: p₁₀ = ∫^τ_u=0 Ҏ[ 0 arrivals in T + u ] × f_y(u) du

The pdf f_y(t) has been discovered before ! From the discussion on the non-persistent CSMA protocol, we got: f_y(t) = the probab. density function of y = e^-gτ×δ(t) + g×e^-g(τ-t) See: click here

Therefore: p₁₀ = ∫^τ_u=0 Ҏ[ 0 arrivals in T + u ] × (e^-gτ×δ(u) + g×e^-g(τ-u)) du ***** Notice that u is a constant !!!

The probability of k arrivals in t sec in a Poisson process is: (gt)^k Ҏ[ k arrivals in t sec ] = ---- e^-gt k!
So the probability of 0 arrivals in T+u sec in a Poisson process is: (g(T+u))⁰ Ҏ[ 0 arrivals in T+u sec ] = ----------- e^-g(T+u) = e^-g(T+u) 0!

Therefore: p₁₀ = ∫^τ_u=0 e^-g(T+u) × (e^-gτ×δ(u) + g×e^-g(τ-u)) du (Split off the discontinuous point u=0) = e^-g(T+0) × e^-gτ + ∫^τ_u=0+ e^-g(T+u) × g×e^-g(τ-u) du = e^-g(T+τ) + ∫^τ_u=0+ e^-g(T+u) × g × e^-g(τ-u) du

Use Maple to compute the integral: > f := g*exp(-g*(tau-u))*exp(-g*(T+u)); f := g exp(-g (tau - u)) exp(-g (T + u)) > integrate(f, u=0..tau); tau g exp(-g tau - g T)

Therefore: p₁₀ = e^-g(T+τ) + gτ e^-g(T+τ) = (1 + gτ) e^-g(T+τ) ................... (9)

We now only have to compute p₁₁ before we can find the throughput formula for the 1-persistent CSMA protocol....

Computing the transition probability p₁₁

Transition from state 1 to state 1:

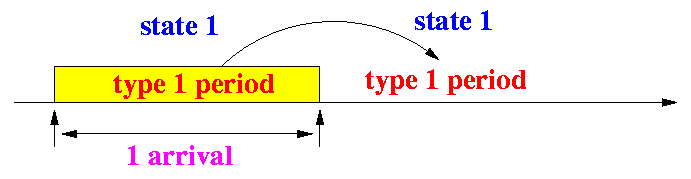
Note:

The system moves from state 1 to state 1 when there is exactly 1 arrival in the type 1 period
Again, the number of arrivals in the type 1 period depends on the duration (length) of the type 1 period

To obtain the duration of the type 1 period, we must look at the anatomy of a type 1 transmission period:

Suppose a type 1 period is started at time t by the packet transmission x:

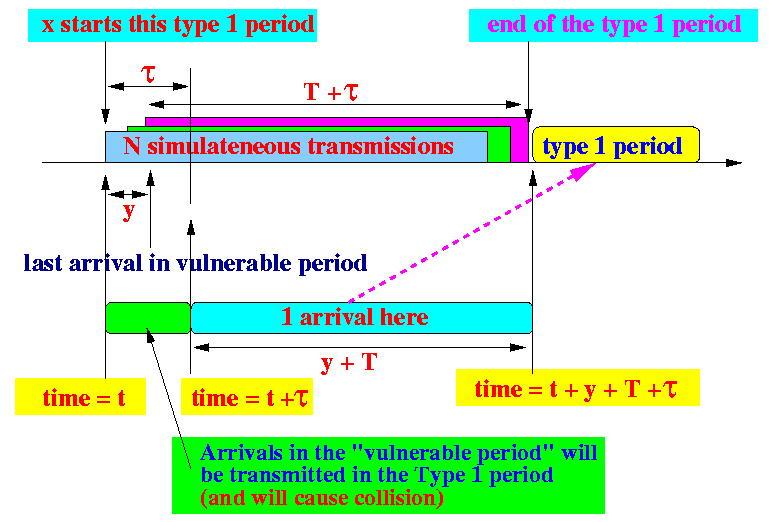
Observation 1:

Arrivals that arrive before time t + τ will not detect the starting transmission x
Consequently, they will schedule themselves for transmission within the type 1 period (and they will cause a collision)
Arrivals that arrive after time t + τ will detect the starting transmission x
Consequently, they will schedule themselves for transmission after the type 1 period

Observation 2:

The total length of the type 1 period is T + τ + y
(y is the time of the last arriving packet before deadline τ)
In order to transit to a type 1 period, there must be one (1) arrival between: [t + τ, t + y + T + τ)
I.e., there must be one (1) arrivals in (T + y) sec

Thus: the probability that a state 1 period will transits into a type 0 period is equal to:

p₁₁ = Ҏ[ 1 arrival in (T + y) sec ]

Again, if y were a constant, the solution would be simple:

(g(T + y))¹ ---------- e^{-g(T + y)} (Poisson arrivals) 1!

BUT, y is a random variable

We will need use the Law of Total Probability to compute Ҏ[ 0 arrivals in (T + y) sec ]:

(We divide the range "[0, τ]" into individual time instances u)

p₁₁ = ∑^τ_u=0 Ҏ[ 1 arrival in T + y | y = u ] × Ҏ[ y = u ] (Law of Tatal Probability) = ∑^τ_u=0 Ҏ[ 1 arrival in T + u ] × Ҏ[ y = u ]
The sum is in fact an integral because the random variable y is a continuous random variable: p₁₁ = ∫^τ_u=0 Ҏ[ 1 arrival in T + u ] × f_y(u) du Again, the difference is the variable u is NOT a random variable

From the discussion on the non-persistent CSMA protocol, we got: f_y(t) = the probab. density function of y = e^-gτ×δ(t) + g×e^-g(τ-t) See: click here

Therefore: p₁₁ = ∫^τ_u=0 Ҏ[ 1 arrival in T + u ] × (e^-gτ×δ(u) + g×e^-g(τ-u)) du

The probability of k arrivals in t sec in a Poisson process is: (gt)^k Ҏ[ k arrivals in t sec ] = ---- e^-gt k!
So the probability of 1 arrival in T+u sec in a Poisson process is: (g(T+u))¹ Ҏ[ 1 arrivals in T+u sec ] = ----------- e^-g(T+u) = g(T+u)e^-g(T+u) 1!

Therefore: p₁₁ = ∫^τ_u=0 g(T+u) e^-g(T+u) × (e^-gτ×δ(u) + g×e^-g(τ-u)) du (Split off the discontinuous point u=0) = g(T+0) e^-g(T+0) × e^-gτ + ∫^τ_u=0+ g(T+u) e^-g(T+u) × g×e^-g(τ-u) du = gT e^-g(T+τ) + ∫^τ_u=0+ g(T+u) e^-g(T+u) × g × e^-g(τ-u) du

Use Maple to compute the integral: > f := g*(T+u)*g*exp(-g*(tau-u))*exp(-g*(T+u)); 2 f := g (T + u) exp(-g (tau - u)) exp(-g (T + u)) > integrate(f, u=0..tau); 2 1/2 tau (2 T + tau) g exp(-g tau - g T)

Therefore: p₁₁ = gT e^-g(T+τ) + 1/2 τ (2 T + τ) g² e^-g(T+τ) = gT e^-g(T+τ) + τ (T + τ/2) g² e^-g(T+τ) (Take g e^-g(T+τ) out) = g e^-g(T+τ) (T + τ (T + τ/2) g ) = g e^-g(T+τ) (T + gτ(T + τ/2)) ................... (10)

Finally: throughput expression for 1-persistent CSMA

Substitute the equations (2), (4), (5), (6), (7), (8), (9), (10) in equation (1) and after a lot of Mathematical manipulations, we will find:

gT e^-g(T+2τ) [ 1 + gT + gτ(1 + gT + gτ/2) ] S = -------------------------------------------- ........ (11) g(T + 2τ) - (1 - e^-gτ) + (1 + gτ)e^-g(T+τ)

The normalized throughput expression for 1-persistent CSMA

Often, we see the normalized form (normalized by packet transmission time T)

Substitutions used to normalize the throughput expression:

g = offered packet rate per sec G = gT ....... (11) = offered packet rate per packet transmission time T
τ = end to end propagation delay in sec τ a = --- ....... (12) T = end to end propagation delay in packet transmission time T
A useful derived equality: a = τ/T <=> aT = τ <=> agT = gτ <=> aG = gτ

Normalized throughput expression:

gT e^-g(T+2τ) [ 1 + gT + gτ(1 + gT + gτ/2) ] S = -------------------------------------------- ........ (11) g(T + 2τ) - (1 - e^-gτ) + (1 + gτ)e^-g(T+τ) gT e^-(gT+2gτ) [ 1 + gT + gτ(1 + gT + gτ/2) ] = -------------------------------------------- (Subst: G = gT) (gT + 2gτ) - (1 - e^-gτ) + (1 + gτ)e^-(gT+gτ) G e^-(G+2gτ) [ 1 + G + gτ(1 + G + gτ/2) ] = ------------------------------------------ (Subst: aG = gτ) (G + 2gτ) - (1 - e^-gτ) + (1 + gτ)e^-(G+gτ) G e^-(G+2aG) [ 1 + G + aG(1 + G + aG/2) ] = ------------------------------------------ (Rewrite nicer...) (G + 2aG) - (1 - e^-aG) + (1 + aG)e^-(G+aG) G e^-G(1+2a) [ 1 + G + aG(1 + G + aG/2) ] = ------------------------------------------ ......... (12) G(1 + 2a) - (1 - e^-aG) + (1 + aG)e^-G(1+a)

This is the classic form for the throughput of 1-persistent CSMA

Performance graphs
- Performance graphs:
Comparing with Non-persistent CSMA...
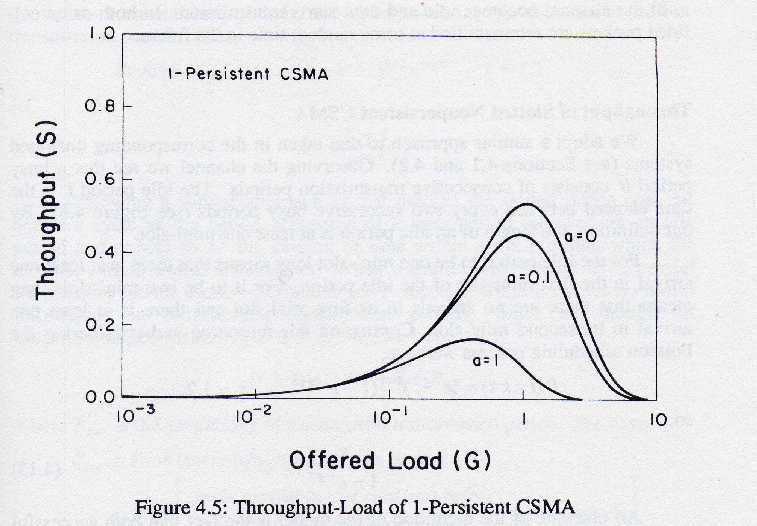
- Comparing Performance:
  1-persistent CSMA performs slightly better at lighter loads