---

Summary: Analysis of 802.11

---

• The 802.11 protocol
  • Protocol summary:

    Sense channel before transmitting a packet If channel is clear: Transmit packet Wait for ACK If ACK is not received within a time out period, assume collision (i.e.: back off) If channel is busy: Back off          Back off protocol: Select a random number (range of the randon numbers is increasing exponentially) Decrement count down counter when the channel is idle

  ---

  ---

• Overview of the performance analysis of the 802.11 protocol
  • The analysis procedure consists of 2 parts:

    Find τ = the steady state probability that a station transmits a packet in a arbitrary slot time FInd the fraction of slots that are successful

  ---

  ---

• Find τ = probability that a station will transmit
  • State transition diagram:

    ---

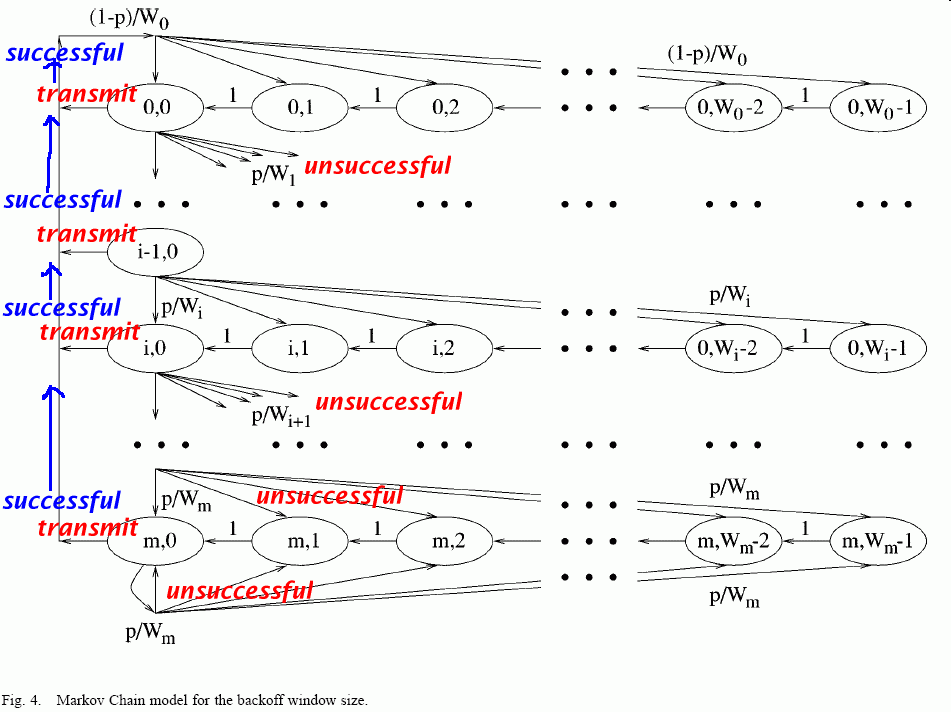
  • The probability τ that a station transmits a packet is equal to:

    τ = b0,0 + b1,0 + ... + bm,0 (bi,j = the steady state probability that the system is in state (i,j))

    ---

  • The equilibrium (steady state) equations obtained from the (Markov) state transition diagram:

    b1,0 = p × b0,0 .... (E1a) b2,0 = p2 × b0,0 .... (E1b) b3,0 = p3 × b0,0 .... (E1c) ... bm-1,0 = pm-1 × b0,0 .... (E1x) pm bm,0 = ----- × b0,0 ....... (E3) 1-p (Wi - k) bi,k = --------- × p × bi-1,0 (for i = 1, 2, ..., m-1 and k > 0) ........ (E4) Wi (Wm - k) bm,k = --------- × p × (bm-1,0 + bm,0) (for k > 0) ...... (E5) Wm W0 - k b0,k = -------- × (1-p) × (b0,0 + b1,0 + .... + bm,0) ...... (E6) W0

    ---

  • The solution for b_i,j in terms of b_0,0

    b1,0 = p × b0,0 .... (E1a) b2,0 = p2 × b0,0 .... (E1b) b3,0 = p3 × b0,0 .... (E1c) ... bm-1,0 = pm-1 × b0,0 .... (E1x) pm bm,0 = ----- × b0,0 ....... (E3) 1-p (Wi - k) bi,k = --------- × pi × b0,0 (for i = 1, 2, ..., m-1 and k > 0) ........ (E7) Wi (Wi - k) bm,k = --------- × pm × 1/(1-p) × b0,0 ...... (E8) Wi W0 - k b0,k = -------- × b0,0 ....... (E9) W0

    with b_0,0 equal to:

    ---

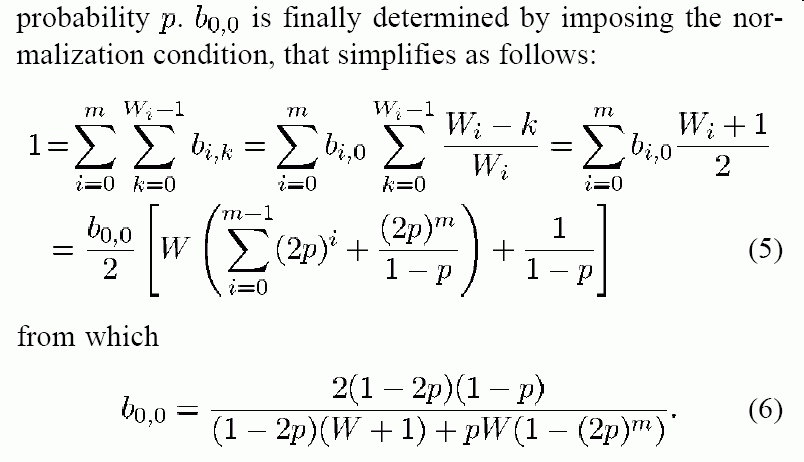
  • τ is equal to:

  ---

  ---

  ---

  ---

• Probability of a successful/unsuccessful transmission
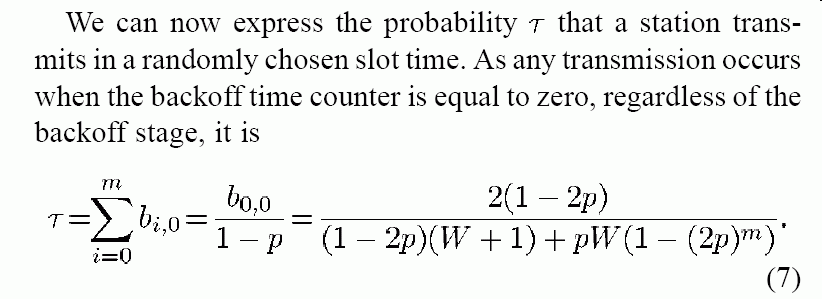
  • Probability that a transmission is successful:

    Ҏ[ successul transmission] = (1 − τ)n−1

  • p = Probability that a transmission is unsuccessful:

    p = Ҏ[ unsuccessul transmission] = 1 − (1 − τ)n−1

  ---

  ---

• Finding τ and p
  • τ and p can be found by solving this non-linear system:

    2(1-2p) τ = ---------------------------- ...... (7) (1-2p)(W+1) + pW(1 - (2p)m) p = 1 - (1-τ)n-1 ...... (9)

  ---

  ---

  ---

  ---

• Throughput of 802.11 - Preliminary Analysis
  • In general, a transmission channel goes through the following cycles:

    ---

  • Therefore, the normalized throughput can always be expressed as follows:

    Total amount of useful time S = -------------------------------- Total amount of time Or: Avg. length of the payload in a slot × Ҏ[ slot contains exactly one transmission ] S = ---------------------------------------------------------------------------------------- Avg. length of a slot E[P] × Ptr × Ps = ------------------------- Avg. length of a slot where: Ptr = probability that a slot contains a transmission Ps = probability that transmission is successful E[P] = Avg. length of the payload in a slot

    With:

    Ptr = Ҏ[ at least 1 terminal transmit ] = 1 - (1 - τ)n

    and:

    Ps = Ҏ[ a transmission is successful ] n τ (1 - τ)n-1 = ----------------- 1 - (1 - τ)n

    (E[P] was assumed to be constant (because I did not want to deal with variable packet length)

  ---

  ---

• Average length of a slot
  • Avg. length of a slot:

    Avg. length of a slot = Weighted average of the length of the 3 diff. kinds of slot = Ҏ[ 0 transmission ] × σ + Ҏ[ 1 transmission ] × Ts + Ҏ[ > 1 transmission ] × Tc = (1 - Ptr)×σ + (PtrPs)×Ts + (Ptr(1-Ps))×Tc

    where:

    Ts = Avg. length of a slot when the slot contains a successful transmission Tc = Avg. length of a slot when the slot contains a unsuccessful transmission (collision)             σ = "empty slot time", time needed for a station to detect the transmission (of a packet) from any other station         (This value is like the end-to-end propagation delay on an Ethernet network)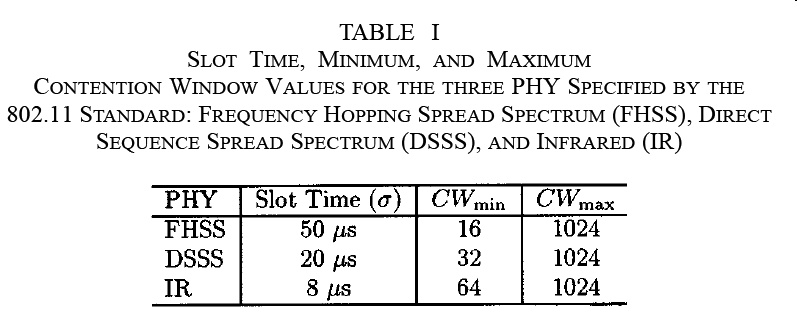

  ---

  ---

• The values T_s and T_c in the basic access method
  • The following figure shows a successful and an unsuccessful transmission using the basic access method:

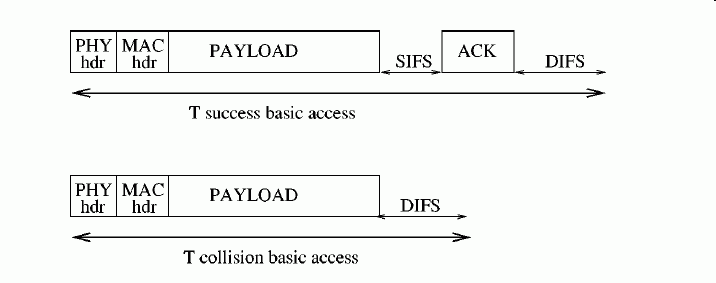
  • Therefore:

    Ts = ( H + E[P] + SIFT + δ ) + ( ACK + DIFS + δ ) ..... (6) Tc = H + E[P] + DIFT + δ ..... (7)

  ---

  ---

• The values T_s and T_c in the RTS/CTS access method
  • The following figure shows a successful and an unsuccessful transmission using the RTS/CTS access method:

  • Therefore:

    Ts = ( RTS + SIFT + δ ) + ( CTS + SIFT + δ ) + ( H + E[P] + SIFT + δ ) + ( ACK + DIFS + δ ) ..... (8) Tc = RTS + DIFT + δ ..... (9)