- Algorithm to
construct
a full reducer for
an acyclic hypergraph:
Let H be the hypergraph of the relations involved in a multi-way join FullReducer( hypergraph H ) { if ( H has 1 hyper-edge ) { done } else { Let E be an ear of H; Let G be the hyperedge that consumes E; Executes: E := E ⋉ G FullReducer( G − E ); // Ear reduction Executes: G := G ⋉ E } }
- Example:
- Multi-way
join operation:
R(A, B, C) ⋈ S(C, D, E) ⋈ T(A, E, F) ⋈ U(A, C, E)
Objective:
- Find a full reducer for
the relations
R,
S,
T and
U
(that will remove all dangling tuples from these relations)
- Find a full reducer for
the relations
R,
S,
T and
U
- The hyper-graph for the
join-operation
R(A, B, C) ⋈
S(C, D, E) ⋈
T(A, E, F) ⋈ U(A, C, E)
is:

- A full reducer for
R,
S,
T and
U can be
constructed as
follows:
FullReducer( {R,S,T,U} ) = T is an ear edge U consumes T Executes: U := U ⋉ T FullReducer( {R,S,T,U} − T ) Executes: T := T ⋉ U
- A full reducer for the
reduced hyper-graph
R,
S and
U:

can be constructed as follows:
FullReducer( {R,S,U} ) = R is an ear edge U consumes R Executes: U := U ⋉ R FullReducer( {R,S,U} − R ) Executes: R := R ⋉ U
- A full reducer for the
reduced hyper-graph
S and
U:

can be constructed as follows:
FullReducer( {S,U} ) = S is an ear edge U consumes S Executes: U := U ⋉ S FullReducer( {S,U} − S ) Executes: S := S ⋉ U
- Therefore, a
full reducer is:
U := U ⋉ T U := U ⋉ R U := U ⋉ S S := S ⋉ U R := R ⋉ U T := T ⋉ Uor without the indentation:
U := U ⋉ T U := U ⋉ R U := U ⋉ S S := S ⋉ U R := R ⋉ U T := T ⋉ U
- Multi-way
join operation:
- Claim:
- The algorithm (above) will produce a full reducer for any acyclic hyper-graph
Proof: by induction
- Induction basis:
- The hyper-graph has 1 hyper-egde
Then:
- There is 1 relation in the
join operation
- The singleton relation has trivially no dangling tuples
- Induction step:
- Induction assumption:
- The algorithm (above) will produce a full reducer for any acyclic hyper-graph Hn of n hyper-edges
- Let Hn+1 be
a hyper-graph with
n+1 hyper-edges
Let E be an ear edge of Hn+1
Let G be the consuming edge of E
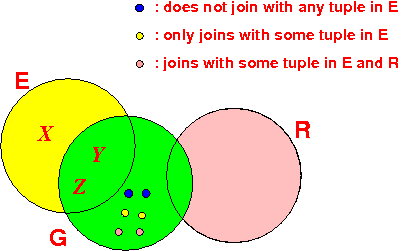
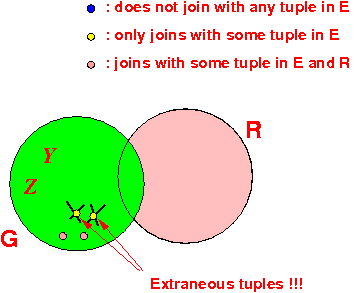
Notice the 3 classes of tuples in relation G:
- Tuples that do
not join with
any tuple in
E
- Tuples that
join with
(at least one) tuple in
E
(and do
not join with
any tuple in
other relations (R)
- Tuples that join with (at least one) tuple in E and with (at least one) tuple in another relations (R)
Then:
- The semi-join
G := G ⋉ E will:
- eliminates
all tuples ∈ G that
does not join with
at least one tuple ∈ E
- I.e.: eliminates all dangling tuples ∈ G with respect to the relation E
Result:
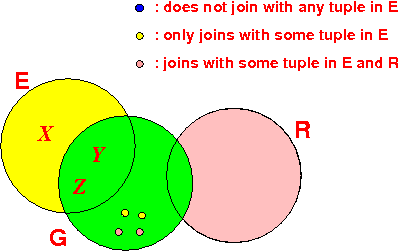
Notice that:
- Tuples ∈ E will
not join with
tuples
in other relations
(= other than G) !!!
Therefore:
- We can removing E and consider the smaller hyper-graph without missing dangling tuples in other relation (= other than G) !!!
- However:
now is
not the
right time to
perform:
E := E ⋉ Gbecause:
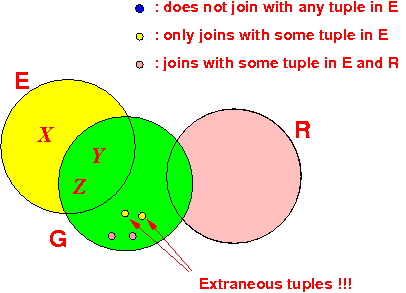
Explanation:
- G can have
extraneous tuples that
only join with
E
- The tuples in E must not be join with the extraneous tuples !!!
- G can have
extraneous tuples that
only join with
E
- eliminates
all tuples ∈ G that
does not join with
at least one tuple ∈ E
- Let's remove E from
Hn:
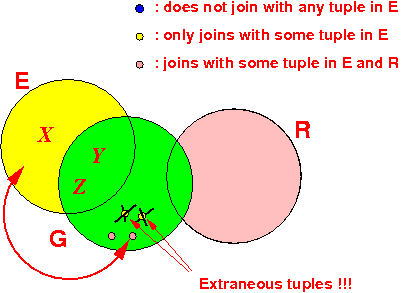
Hn = Hn+1 − EGraphically:
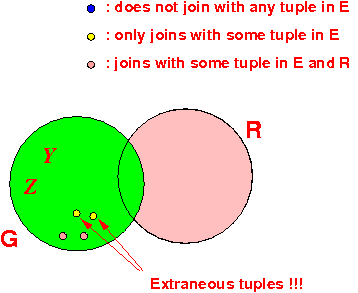
Because:
- Tuples ∈ E does
not affect
other relation beside G
- We have already remove dangling tuples ∈ G with respect to E
Then by the induction hypothesis:
- The semi-joins obtained from FullReducer( Hn ) will remove all dangling tuples in all participanting relations
Graphically:
Notice that:
- Now the relation G is minimal !!!
- Tuples ∈ E does
not affect
other relation beside G
- Therefore, the
semi-join:
E := E ⋉ G
will now remove all dangling tuple from E
Graphically:
- Tuples that do
not join with
any tuple in
E
- Induction assumption: