- Show the content that a
web browser
(such as firefox) will
receive when you enter the following
URL in the browser:
http://www.mathcs.emory.edu/~cheungAnswer:
Type: telnet www.mathcs.emory.edu 80 GET http://www.mathcs.emory.edu/~cheung HTTP/1.0 <ENTER> <ENTER> You will received this message: <html><head> <title>301 Moved Permanently</title> </head><body> <h1>Moved Permanently</h1> <p>The document has moved <a href="http://webhome2.mathcs.emory.edu/~cheung/">here</a>.</p> <hr> <address>Apache/2.0.63 (Unix) DAV/2 mod_ssl/2.0.63 OpenSSL/0.9.7d Server at webhome2.mathcs.emory.edu Port 80</address> </body></html>
- Show in the figure below a sine wave that has the frequency of 1000 Hz
(1 msec = 1 milli second = 0.001 sec):
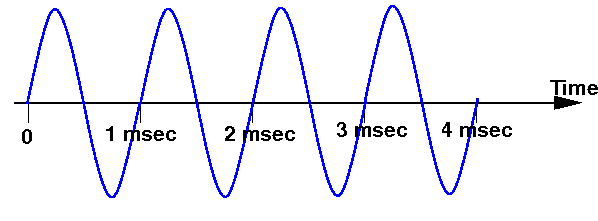
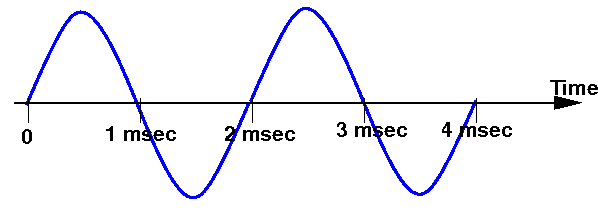
- Show in the figure below a sine wave that has the frequency of 500 Hz:
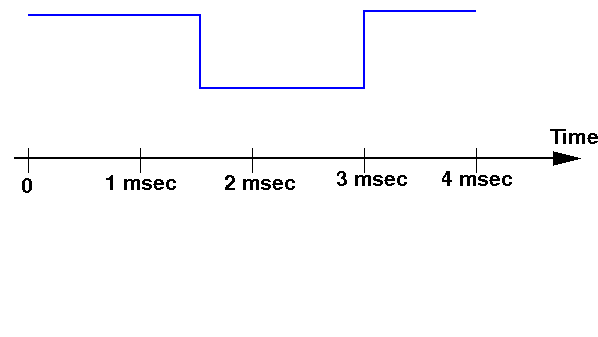
- Consider the following input signal:
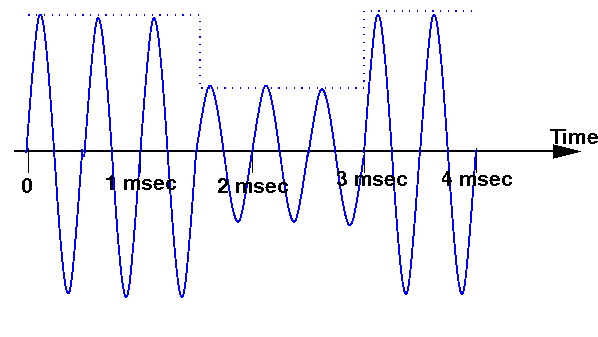
Show the resulting when the input signal is modulated onto a 2000 Hz sine wave using amplitude modulation:
- Suppose you want to improve the quality of transmission of
voice over the telephone by
transmitting all
frequencies
between
20 Hz and
8000 Hz over
a digital transmission channel
What sampling rate do you need to use to re-construct the voice input reliably ? (10 pts)
You need to sample at the Nyquist rate: 2 × 8000 = 16,000 HzEach sample is represented by an integer value between -64 and 63.
What is the data rate of a voice transmission using the above scheme: (10 pts)
1 sample is represented by 7 bits (-64 to 63 = 128 values) 16,000 samples per sec will produce: 16,000 × 7 = 112000 bits / sec
- A sender uses
NRZ
to transmit an (long) serie of
bits to
a receiver.
The receiver reads the transmission at precisely the middle of its clock to determine the value of the transmitted bit.
The sender's clock runs at 1000 Hz and the receiver's clock runs at 999 Hz.
Suppose the receiver does not re-synchronize its clock to the sender's clock.
If the sender's and the receiver's clocks are synchronized at the start of a (long) transmission, which bit poistion is the first bit that the receiver will receive incorrectly due to the clock drift ?
Answer: click here
- Show the digital signal
using NRZ when you transmit
the following data:
- 10110010 (3pts)
Answer: click here
- Show the digital signal
using NRZ when you transmit
the following data:
- 10110010 (3pts) using 4B/5B (4 pts)
Answer: click here
- Show the digital signal
using Manchester code when you transmit
the following data:
- 10110010 (3pts)
Answer: click here
- Transmit the data 1010 using
a 2-level
amplitude modulation where
the 0 bits have
half the
amplitude
of the 1 bits
Use 4 units in the graph below to transmit each bit
Use 2 sine waves for each bit
Answer: (3 ots)
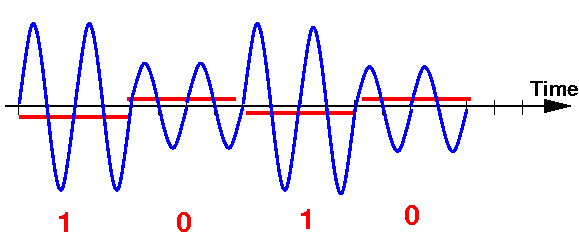
- Transmit the data 1010 using
a 2-level
frequency modulation where
the 0 bits have
half the
frequency
of the 1 bits
Use 4 units in the graph below to transmit each bit
Use 2 sine waves to transmit a 0 bit and 4 sine waves to transmit a 1 bit
Answer: (3 pts)
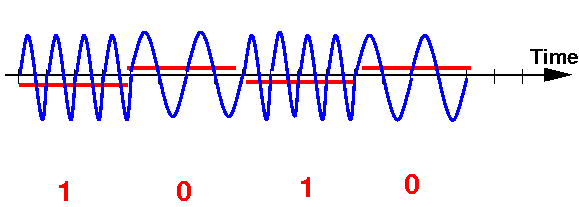
- Transmit the data 1010 using
a 2-level
phase modulation where
the 0 bits have
0 phase shift and
the 1 bits have
180 degrees phase shift
Use 4 units in the graph below to transmit each bit
Use 2 sine waves to transmit a each bit
Answer: (4 pts)

- Suppose that
the bandwdith of
optical fiber is 1 GHz
If the the signal to noise ratio is 100, what is the maximum data transmission rate on this optical fiber: (5 pts)
MAx data rate = Bandwidth × 2log(1 + S/N) = 1,000,000,000 × 2log(1 + 100) = 1,000,000,000 × 6.658 = 6,658,000,000 bits / sec = 6.658 Gbps
If the the signal to noise ratio is 1000, what is the maximum data transmission rate on this optical fiber: (5 pts)
Max data rate = Bandwidth × 2log(1 + S/N) = 1,000,000,000 × 2log(1 + 1000) = 1,000,000,000 × 9.967 = 9,967,000,000 bits / sec = 9.967 Gbps