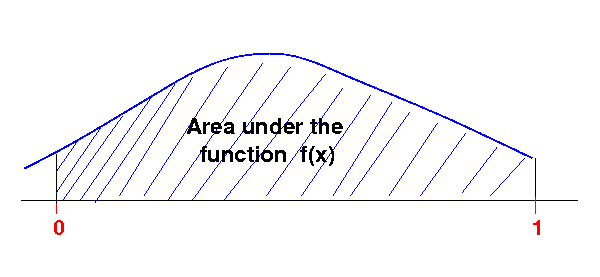
Computing π with numerical integration

  • One of the many ways to compute the value of π is: 

             1
   π =  ∫ (2.0/sqrt(1 - x*x))  dx 
        0

  • You can prove this equality by compute the integral using Matlab as follows: 

       >> syms x
   >> int( 2/sqrt(1-x*x), 0, 1 )
   ans = pi

  • We will use this integral to compute an approximation for π using:

    • Numerical integration

DEMO: matlab -nodesktop

Numerical integration

  • The integral: 

       1
  ∫ f(x)  dx 
  0

    is equal to the area under the function f(x) between the points x = 0 and x = 1:
     

Numerical integration

  • The integral: 

       1
  ∫ f(x)  dx 
  0

    can be approximated by the sum of the area of N rectangles:

    The width of each rectangle w = 1/N.

Numerical integration

  • The area of the first rectangle: 

       1
  ∫ f(x)  dx  ~= w*f(0.5w) + ...
  0

    is equal to   w × f(0.5w):

    The width = w and the height = f(0.5w)

Numerical integration

  • The area of the 2nd rectangle: 

       1
  ∫ f(x)  dx  ~= w*f(0.5w) + w*f(1.5w) + ...
  0

    is equal to   w × f(1.5w):

    The width = w and the height = f(1.5w)

Numerical integration

  • The sum of the area of N rectangles is: 

       1
  ∫ f(x)  dx  ~= w*f(0.5w) + w*f(1.5w) + ... + w*f( (N-1)+0.5)*w )
  0

    which can be computed numerically

    Note:   the approximation is better when N is larger....

Numerical integration

  • The integral: 

       1
  ∫ f(x)  dx  ~= w*f(0.5w) + w*f(1.5w) + ... + w*f( (N-1)+0.5)*w )
  0

    can be approximated numerically as follows: 

       Integral = 0;

   w = (1 - 0)/N;    // The width of each rectangle

   for (int i = 0; i < N; i++)
   {
      x = (i+0.5)*w;
      Integral = Integral + w * f(x); // w * f(x) is area of rectangle
   }

  • This algorithm is called the "Rectangle Rule" in Numerical Analysis...

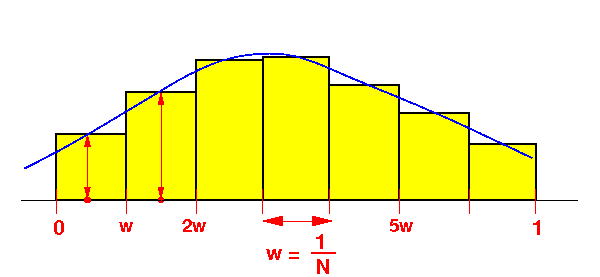
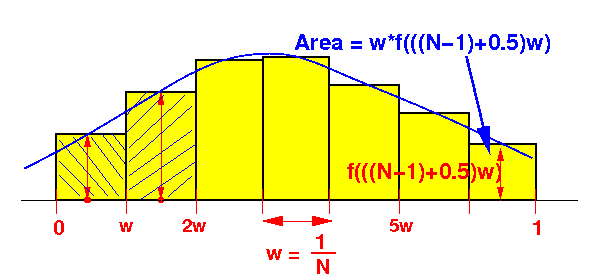
Approximating π using the Rectangle Rule

  • The Rectangle Rule algorithm in C used to approximate π: 

    double f(double x)
{
    return( 2.0 / sqrt(1 - x*x) ); // Used to approximate pi
}

int main(int argc, char *argv[])
{
    int    i;
    int    N;
    double sum;
    double x, w;

    N = ...;     // N will determine the accuracy of the approximation
    w = 1.0/N;   // a = 0, b = 1, so: (b-a) = 1.0

    sum = 0.0;

    for (i = 0; i < N; i++)
    {
        x = (i + 0.5) * w;
        sum = sum + w*f(x);
    }

    printf("Pi = %lf", sum);
}

DEMO: demo/pthread/compute-pi.c

Common technique to parallelize program with multi-threaded program

  • How to parallelize a single-threaded program:

    • Consider program segments where work can be performed concurrently

  • Good place to look:

    • Loops !!!

  • Example of a loop that can be parallelized: 

       for (i = 0; i < N; i = i + 1)
   { 
      x = w*(i + 0.5);    
      sum = sum + w*f(x);
   }

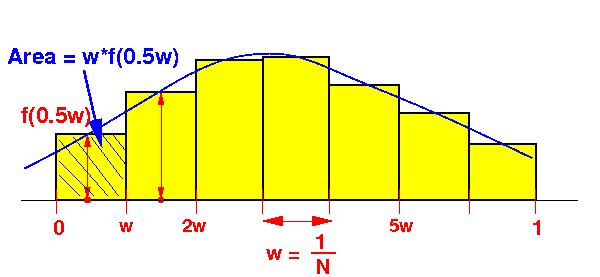
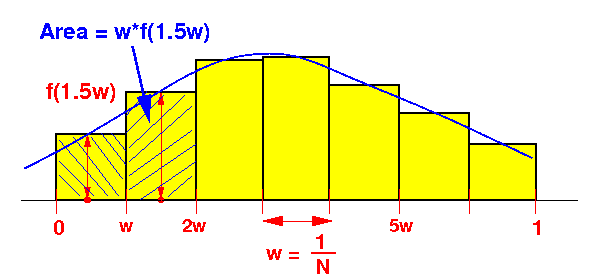
   Loop computes:

      w*f(0.5w) + w*f(1.5w) + w*f(2.5w) + ... + w*f( (N-1)+0.5)*w )

Parallelizing loops with multi-threaded programming

  • Example of a loop that can be parallelized with multi-threaded programming: 

       for (i = 0; i < N; i = i + 1)
   { 
      x = w*(i + 0.5);    
      sum = sum + w*f(x);
   }

   Loop computes:

      w*f(0.5w) + w*f(1.5w) + w*f(2.5w) + ... + w*f( (N-1)+0.5)*w )

  • Traditional work load distribution between 2 threads: 

    

      values added by thread 0          values added by thread 1
   |<----------------------------->|<----------------------------->|  




  Thread 0 computes: w*f(0.5w) + w*f(1.5w) + .... w*f(0.5-0.5w)

  Thread 1 computes: w*f(0.5+0.5w) + w*f(0.5+1.5w) + ... + w*f(1.0+0.5w)

Parallelizing loops with multi-threaded programming

  • Example of a loop that can be parallelized with multi-threaded programming: 

       for (i = 0; i < N; i = i + 1)
   { 
      x = w*(i + 0.5);    
      sum = sum + w*f(x);
   }

   Loop computes:

      w*f(0.5w) + w*f(1.5w) + w*f(2.5w) + ... + w*f( (N-1)+0.5)*w )

  • Alternate way to distribute the work load between 2 threads ( easier to code): 

                    values added by thread 0
   |   |   |   |   |   |   |   |   |   |   |   |   |   |
   V   V   V   V   V   V   V   V   V   V   V   V   V   V
   |-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|      
     ^   ^   ^   ^   ^   ^   ^   ^   ^   ^   ^   ^   ^   ^
     |   |   |   |   |   |   |   |   |   |   |   |   |   |
                values added by thread 1

  Thread 0 computes: w*f( (0+0.5)w ) + w*f( (2+0.5)w ) + .... 

  Thread 1 computes: w*f( (1+0.5)w ) + w*f( (3+0.5)w ) + ....

Comment:   paging and multi-threaded programming

  • Multi-threaded program that scans of memory data can be affected by paging

    Example: 

                    values accessed by thread 0
   |   |   |   |   |   |   |   |   |   |   |   |   |   |
   V   V   V   V   V   V   V   V   V   V   V   V   V   V
   |-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|      
     ^   ^   ^   ^   ^   ^   ^   ^   ^   ^   ^   ^   ^   ^
     |   |   |   |   |   |   |   |   |   |   |   |   |   |
                values accessed by thread 1

  Thread 0 accesses:   a[0]  a[2]  ...   // Access memory variables

  Thread 1 accesses:   a[1]  a[3]  ...   // Access memory variables

  • However: computation that do not access memory is not affected by paging: 

      Thread 0 computes: w*f( (0+0.5)w ) + w*f( (2+0.5)w ) + .... 

  Thread 1 computes: w*f( (1+0.5)w ) + w*f( (3+0.5)w ) + ....

Multi-threaded program to compute the approximation π using the Rectangle Rule

  • Recall the single-threaded program in C to approximate π: 

    int main(int argc, char *argv[])
{
    int    i;
    int    N;        // <----- Share this variable
    double sum;      // <----- Share this variable
    double x, w;

    N = ...;     // N will determine the accuracy of the approximation
    w = 1.0/N;   // a = 0, b = 1, so: (b-a) = 1.0

    sum = 0.0;

    for (i = 0; i < N; i++)
    {
        x = (i + 0.5) * w;
        sum = sum + w*f(x);
    }







}

Multi-threaded program to compute the approximation π using the Rectangle Rule

  • We must make N and sum shared variables because they are used by all threads: 

    int    N;    // # intervalues              Shared variables
double sum;  // Sum of rectangles



int main(int argc, char *argv[])
{
    N = ...;     // N will determine the accuracy of the approximation

    sum = 0.0;

 
    
        

    Create threads to do the work...





    Wait for threads to finish...


}

Multi-threaded program to compute the approximation π using the Rectangle Rule

  • Create num_threads threads to do the work: 

    int    N;    // # intervalues              Shared variables
double sum;  // Sum of rectangles
int num_threads; // # Threads used


int main(int argc, char *argv[])
{
    N = ...;     // N will determine the accuracy of the approximation
 
    sum = 0.0;

    num_threads = ...;    // # threads used

    pthread_t tid[100];   // Used for pthread_join()
    int id[100];          // Start index values for each thread

    for (int i = 0; i < num_threads; i++) 
    {
        id[i] = i; 
        pthread_create(&tid[i], NULL, PIworker, &id[i]); 
    }



}

Multi-threaded program to compute the approximation π using the Rectangle Rule

  • Wait for all threads to complete: 

    int    N;    // # intervalues              Shared variables
double sum;  // Sum of rectangles
int num_threads; // # Threads used


int main(int argc, char *argv[])
{
    N = ...;     // N will determine the accuracy of the approximation

    sum = 0.0;

    num_threads = ...;    // # threads used

    pthread_t tid[100];   // Used for pthread_join()
    int id[100];          // Start index values for each thread

    for (int i = 0; i < num_threads; i++) 
    {
        id[i] = i; 
        pthread_create(&tid[i], NULL, PIworker, &id[i]); 
    }

    for (int i = 0; i < num_threads; i = i + 1)  // Wait for threads
        pthread_join(tid[i], NULL);
}

The PIworker( ) function

  • The PIworker(id) function will compute a part of the total sum that starts at index id: 

    int    N;    // # intervalues              Shared variables
double sum;  // Sum of rectangles
int num_threads; // # Threads used


void *PIworker(int *id)
{
    int i, myStart;
    double x;
    double w = 1.0/N;


    myStart = *id;

    Computes:  

       for (i = myStart; i < N; i = i + num_threads)
       {
           x = w * ((double) i + 0.5);     // next x
           sum = sum + w*f(x);             // Add to sum
       }



}

The PIworker( ) function

  • The PIworker(id) function will compute a part of the total sum that starts at index id: 

    int    N;    // # intervalues              Shared variables
double sum;  // Sum of rectangles
int num_threads; // # Threads used


void *PIworker(int *id)
{
    int i, myStart;
    double x;
    double w = 1.0/N;

    /*** Get the parameter (which is my starting index) ***/
    myStart = *id;

    /*** Compute sum, skipping every "num_threads" items ***/
    for (i = myStart; i < N; i = i + num_threads)
    {
        x = w * ((double) i + 0.5);     // next x

        sum = sum + w*f(x);             // Add to sum

    }

    pthread_exit(NULL);
}

DEMO: demo/pthread/compute-pi-mt0.c --- Synchronization error...

Synchronizing the updates in the PIworker( ) function

  • We must use a mutex variable to synchronize the updates to the shared variable sum: 

    int    N;    // # intervalues              Shared variables
double sum;  // Sum of rectangles
int num_threads; // # Threads used
pthread_mutex_t sum_mutex;

void *PIworker(int *id)
{
    int i, myStart;
    double x;
    double w = 1.0/N;

    /*** Get the parameter (which is my starting index) ***/
    myStart = *id;

    /*** Compute sum, skipping every "num_threads" items ***/
    for (i = myStart; i < N; i = i + num_threads)
    {
        x = w * ((double) i + 0.5);     // next x
	pthread_mutex_lock(&sum_mutex);
        sum = sum + w*f(x);             // Add to sum
	pthread_mutex_unlock(&sum_mutex);
    }

    pthread_exit(NULL);
}

Synchronizing the updates in the PIworker( ) function

  • We must initialize the mutex variable in main( ) before creating the threads: 

    pthread_mutex_t sum_mutex;

int main(int argc, char *argv[])
{
    N = ...;     // N will determine the accuracy of the approximation
    w = 1.0/N;   // a = 0, b = 1, so: (b-a) = 1.0

    sum = 0.0;

    pthread_mutex_int(&sum_mutex, NULL);

    num_threads = ...; // # threads used
    pthread_t tid[100];   // Used for pthread_join()
    int id[100];          // Start index values for each thread
    for (i = 0; i < num_threads; i++) 
    {
        id[i] = i; 
        pthread_create(&tid[i], NULL, PIworker, &id[i]); 
    }

    for (i = 0; i < num_threads; i = i + 1)  // Wait for threads
        pthread_join(tid[i], NULL);
}

DEMO: demo/pthread/compute-pi-mt1.c --- Synchronization bottleneck...

Synchronization Bottleneck

  • Simultaneous updates to shared variables can cause:

    • Synchronization bottlenecks in parallel programs

  • Synchronization bottleneck:

    • When parallel executions must wait for each other

    • The parallel executions will behave like a sequential execution

    Example: only one (= 1) thread will be able to execute sum = sum + + w*f(x) 

        for (i = myStart; i < N; i = i + num_threads)
    {
        x = w * ((double) i + 0.5);     // next x
	pthread_mutex_lock(&sum_mutex);
        sum = sum + w*f(x);             // Serial execution !!
	pthread_mutex_unlock(&sum_mutex);
    }

Avoiding synchronized updates

  • Synchronization is required to update shared variable: 

    int    N, num_threads;
double sum;        // <---- Shared variable
pthread_mutex_t sum_mutex;

void *PIworker(int *id)
{
    int i, myStart;
    double x;
    double w = 1.0/N;

    /*** Get the parameter (which is my starting index) ***/
    myStart = *id;

    /*** Compute sum, skipping every "num_threads" items ***/
    for (i = myStart; i < N; i = i + num_threads)
    {
        x = w * ((double) i + 0.5);     // next x
	pthread_mutex_lock(&sum_mutex);
        sum = sum + w*f(x);       // Synchronize access to shared var
	pthread_mutex_unlock(&sum_mutex);
    }


    pthread_exit(NULL);
}

Avoiding synchronized updates

  • Use a local variable to avoid synchronization: 

    int    N, num_threads;
double sum;        // <---- Shared variable
pthread_mutex_t sum_mutex;

void *PIworker(int *id)
{
    int i, myStart;
    double x;
    double w = 1.0/N;

    /*** Get the parameter (which is my starting index) ***/
    myStart = *id;

    int mySum = 0.0;    // <---- Not shared 
    for (i = myStart; i < N; i = i + num_threads)
    {
        x = w * ((double) i + 0.5);     // next x
        mySum = mySum + w*f(x);  // Use local var to avoid synchr
    }




    pthread_exit(NULL);
}

Avoiding synchronized updates

  • Add the final total using a synchronized update: 

    int    N, num_threads;
double sum;        // <---- Shared variable
pthread_mutex_t sum_mutex;

void *PIworker(int *id)
{
    int i, myStart;
    double x;
    double w = 1.0/N;

    /*** Get the parameter (which is my starting index) ***/
    myStart = *id;

    int mySum = 0.0;    // <---- Not shared 
    for (i = myStart; i < N; i = i + num_threads)
    {
        x = w * ((double) i + 0.5);     // next x
        mySum = mySum + w*f(x);  // Use local var to avoid synchr
    }
    pthread_mutex_lock(&sum_mutex);
    sum = sum + mySum;       // Synchronize access to shared var
    pthread_mutex_unlock(&sum_mutex);

    pthread_exit(NULL);
}

DEMO: demo/pthread/compute-pi-mt2.c