Review: Categories of digital circuits

The digital circuits are divided into 2 broad categories:

  1. Combinatorial digital circuits:

      • The output signals depend only on the current values of the input signals

        I.e.: circuit has no memory

  2. Sequential digital circuits:

      • The output signals depend on (1) the current values of the input signals and (2) the state of the (digital) circuit

        I.e.: circuit has memory

 

We will now study how to design (= make) combinatorial circuits that perform a certain function

Making connection between circuit components (e.g.: gates)

  • Background information for non Electrical Engineering majors:

      • An output of a circuit emits an electrical current (active)

      • An input of a circuit can receive an electrical current (passive)

      • An output of a circuit cannot receive an electrical current

        (There is an exception to this rule for the "Open Collector" output that will be discussed later)

  • Consequence:

                     

      • Two outputs must not be connected with each other !!!      

        (It will cause a short ciruit)

Making connection between circuit components (Summary)

Example of legal and illegal connection between circuit elements:

 

 

 

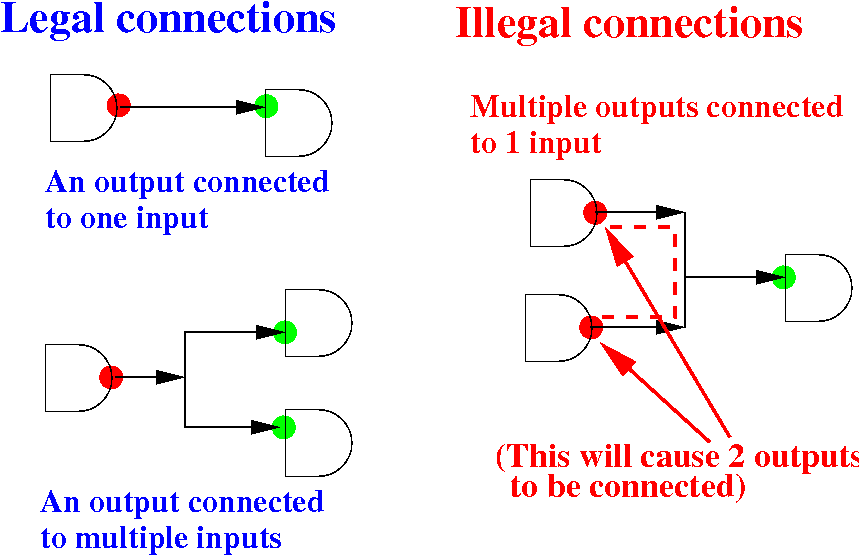
Note: later in the course, you will learn about a "high impedance" output circuit that can be connected together.

Example: connecting circuit components

Example of a (digital) circuit:

 

 

  • An output can be connected to (one or more) inputs

  • An input can only be connected to one output

Example of a combinatorial circuit
 

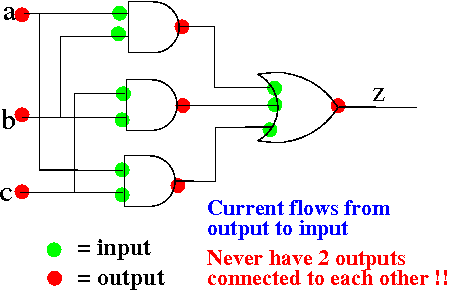
Consider the following circuit with input signals: a, b, c and output signal: z:

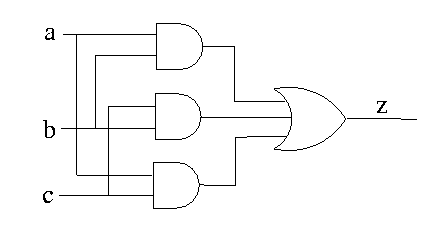
Can you figure out the function performed by the following circuit ?

DEMO: /home/cs355001/demo/circuits/circuit1

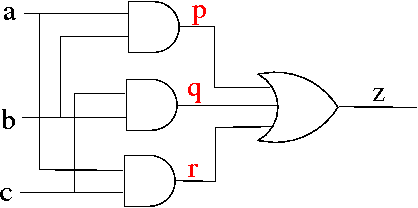
Finding the value of output z for every input value combinarion 

          a  b  c  | p  q  r | z
     ----------+---------+---- 
      0  0  0  |         |
      0  0  1  |         |
      0  1  0  |         |
      0  1  1  |         |
      1  0  0  |         |
      1  0  1  |         |
      1  1  0  |         |
      1  1  1  |         |

Finding the value of output z for every input value combinarion 

          a  b  c  | p  q  r | z   (p = a AND b)
     ----------+---------+---- 
      0  0  0  | 0       |
      0  0  1  | 0       |
      0  1  0  | 0       |
      0  1  1  | 0       |
      1  0  0  | 0       |
      1  0  1  | 0       |
      1  1  0  | 1       |
      1  1  1  | 1       |

Finding the value of output z for every input value combinarion 

          a  b  c  | p  q  r | z   (q = b AND c)
     ----------+---------+---- 
      0  0  0  | 0  0    |
      0  0  1  | 0  0    |
      0  1  0  | 0  0    |
      0  1  1  | 0  1    |
      1  0  0  | 0  0    |
      1  0  1  | 0  0    |
      1  1  0  | 1  0    |
      1  1  1  | 1  1    |

Finding the value of output z for every input value combinarion 

          a  b  c  | p  q  r | z   (r = a AND c)
     ----------+---------+---- 
      0  0  0  | 0  0  0 |
      0  0  1  | 0  0  0 |
      0  1  0  | 0  0  0 |
      0  1  1  | 0  1  0 |
      1  0  0  | 0  0  0 |
      1  0  1  | 0  0  1 |
      1  1  0  | 1  0  0 |
      1  1  1  | 1  1  1 |

Finding the value of output z for every input value combinarion 

          a  b  c  | p  q  r | z  (z = p OR q OR r)
     ----------+---------+---- 
      0  0  0  | 0  0  0 | 0
      0  0  1  | 0  0  0 | 0
      0  1  0  | 0  0  0 | 0
      0  1  1  | 0  1  0 | 1
      1  0  0  | 0  0  0 | 0
      1  0  1  | 0  0  1 | 1
      1  1  0  | 1  0  0 | 1
      1  1  1  | 1  1  1 | 1

Question: what function does this circuit compute ???

Alternate way to view a circuit: "majority function" circuit 

          a  b  c  | p  q  r | z  (z = p OR q OR r)
     ----------+---------+---- 
      0  0  0  | 0  0  0 | 0
      0  0  1  | 0  0  0 | 0
      0  1  0  | 0  0  0 | 0
      0  1  1  | 0  1  0 | 1
      1  0  0  | 0  0  0 | 0
      1  0  1  | 0  0  1 | 1
      1  1  0  | 1  0  0 | 1
      1  1  1  | 1  1  1 | 1

Output z = 1 if and only if a majority of the input values = 1 !!

Circuit design
 

  • In the previous example, we found out the function of a given circuit

      • Digital circuits can perform/compute very useful functions !!!        

  • In circuit design, we must solve the reverse problem:

      • We are given a specific (useful) function that a circuit must perform/compute

      • The problem is to design a circuit that performs the specified function !

We will study this circuit design problem next