- A matrix is usually stored using a
two-dimensional array
- But in many problems (especially matrices resulting from
discretization), the problem matrix is very sparse
Although sparse matrices can be stored using a two-dimensional array, it is a very bad idea to do so for several reasons:
- The obvious one is wastage of computer memory:
it is not very useful to store many 0 values of the sparse matrix
- The more important reason is runtime speed: by storing the excess (useless) 0 values, the computer program needs to perform unnecessary computations on all the ZERO values. Valuable computer time is wasted and the program runs much slower....
- The obvious one is wastage of computer memory:
it is not very useful to store many 0 values of the sparse matrix
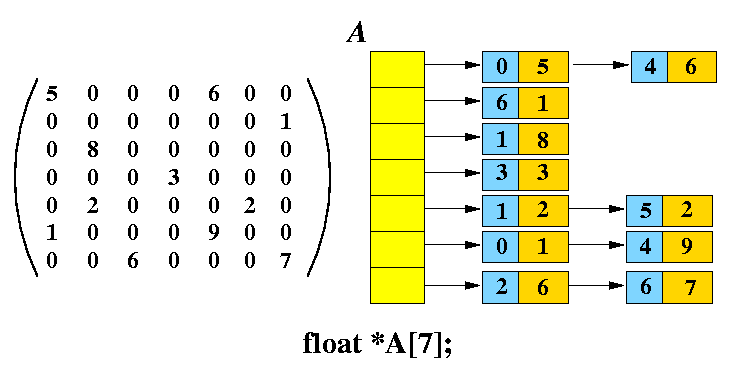
- The linked list can be used to store sparse matrices:
- Sparse matrix can also be used using multiple arrays:
- Coordinate-wise
- Compressed Sparse Row (CSR)
- Compressed Sparse Column (CSC)
- ...
- Each type of representation has its strengths and its weaknesses.
Depending on what operations you want to perform with the sparse matrix, you pick the best representation...
- A sparse matrix is stored using 3 arrays:
- Val[N]: contains the value of the non-zero elements
- Row[N]: contains the row-index of the non-zero elements
- Col[N]: contains the column -index of the non-zero elements
- Val[N]: contains the value of the non-zero elements
- Illustrative Example:
[ 11 12 14 ] [ 22 23 25 ] [ 31 33 34 ] [ 42 45 46 ] [ 55 ] [ 65 66 67 ] [ 75 77 78 ] [ 87 88 ]Representation using Coordinate-wise method: Index 0 1 2 3 4 5 6 7 8 9 10 ----------------------------------------------------------- Val 11 12 14 22 23 25 31 33 34 42 45 Row 0 0 0 1 1 1 2 2 2 3 3 Col 0 1 3 1 2 4 0 2 3 1 4 Index 11 12 13 14 15 16 17 18 19 20 21 ------------------------------------------------------------ Val 46 55 65 66 67 75 77 78 87 88 - Row 3 4 5 5 5 6 6 6 7 7 - Col 5 4 4 5 6 4 6 7 6 7 -
- Properties of the Coordinate-wise method:
- Rows or columns need not be ordered in any way.
- Storage required: nnz floating point, 2*nnz integer.
(nnz = Number of Non-Zero values)
- Accessing the matrix elements by row or column is equally easy.
- Rows or columns need not be ordered in any way.
- Matrix-vector multiplication in the
Coordinate-wise method:
The following code fragment performs the matrix-vector multiplication when the matrix is stored using the Coordinate-wise method:
Multiply matrix (stored in Coordinate-wise method) with vector d[N] for (k = 0; k < N; k = k + 1) result[i] = 0; for (k = 0; k < nnz; k = k + 1) result[Row[k]] = result[Row[k]] + Val[k]*d[Col[k]]; - Sample execution:
Suppose d[0..N-1] = (1, 0, 0, 0, 0, 0, 0, 0) [ 11 12 14 ] [ 1 ] [ 11 ] [ 22 23 25 ] [ 0 ] [ 0 ] [ 31 33 34 ] [ 0 ] [ 31 ] [ 42 45 46 ] X [ 0 ] = [ 0 ] [ 55 ] [ 0 ] [ 0 ] [ 65 66 67 ] [ 0 ] [ 0 ] [ 75 77 78 ] [ 0 ] [ 0 ] [ 87 88 ] [ 0 ] [ 0 ]
After: for (k = 0; k < N; k = k + 1) result[i] = 0; ---> [0, 0, 0, 0, 0, 0, 0, 0] k = 0; result[Row[0]] = result[Row[0]] + Val[0]*d[Col[0]]; result[0] = result[0] + Val[0]*d[0]; result[0] = 0 + 11*1; ---> [11, 0, 0, 0, 0, 0, 0, 0] k = 1; result[Row[1]] = result[Row[1]] + Val[1]*d[Col[1]]; result[0] = result[0] + Val[1]*d[1]; result[0] = 0 + 12*0; ---> [11, 0, 0, 0, 0, 0, 0, 0] k = 2; result[Row[2]] = result[Row[2]] + Val[2]*d[Col[2]]; result[0] = result[0] + Val[2]*d[3]; result[0] = 0 + 14*0; ---> [11, 0, 0, 0, 0, 0, 0, 0] ... k = 6; result[Row[6]] = result[Row[6]] + Val[6]*d[Col[6]]; result[2] = result[2] + Val[6]*d[0]; result[2] = 0 + 31*1; ---> [11, 0, 31, 0, 0, 0, 0, 0]
- A sparse matrix is stored in CSR using 3 arrays:
- Val[N]: contains the value of the non-zero elements
- RowPtr[N]: contains the
row-index range of the non-zero elements
- Col[N]: contains the column-index of the non-zero elements
- Val[N]: contains the value of the non-zero elements
- Illustrative Example:
[ 11 12 14 ] [ 22 23 25 ] [ 31 33 34 ] [ 42 45 46 ] [ 55 ] [ 65 66 67 ] [ 75 77 78 ] [ 87 88 ]Representation using Compressed Sparse Row method: Index 0 1 2 3 4 5 6 7 8 9 10 ----------------------------------------------------------- Val 11 12 14 22 23 25 31 33 34 42 45 RowPtr 0 3 6 9 12 13 16 19 21 - - Col 0 1 3 1 2 4 0 2 3 1 4 Index 11 12 13 14 15 16 17 18 19 20 21 ------------------------------------------------------------ Val 46 55 65 66 67 75 77 78 87 88 - RowPtr - - - - - - - - - - - Col 5 4 4 5 6 4 6 7 6 7 -
- Properties of the Compressed Sparse Row method:
- Requires entries from a row to be consecutively located
in data structure.
- Columns need not be ordered in any way.
- Storage required: nnz floating point, nnz+N+1 integer.
(nnz = Number of Non-Zero values, N = dimension of matrix)
- Row access is easy, but
column access difficult.
- Requires entries from a row to be consecutively located
in data structure.
- Matrix-vector multiplication in the
Compressed Sparse Row method:
The following code fragment performs the matrix-vector multiplication when the matrix is stored using the Compressed Sparse Row method:
Multiply matrix (stored with Compressed Sparse Row method) with vector d[N] for (k = 0; k < N; k = k + 1) result[i] = 0; for (i = 0; i < N; i = i + 1) { for (k = RowPtr[i]; k < RowPtr[i+1]; k = k + 1) { result[i] = result[i] + Val[k]*d[Col[k]]; } } - Sample execution:
Suppose d[0..N-1] = (1, 0, 0, 0, 0, 0, 0, 0) [ 11 12 14 ] [ 1 ] [ 11 ] [ 22 23 25 ] [ 0 ] [ 0 ] [ 31 33 34 ] [ 0 ] [ 31 ] [ 42 45 46 ] X [ 0 ] = [ 0 ] [ 55 ] [ 0 ] [ 0 ] [ 65 66 67 ] [ 0 ] [ 0 ] [ 75 77 78 ] [ 0 ] [ 0 ] [ 87 88 ] [ 0 ] [ 0 ]
After: for (k = 0; k < N; k = k + 1) result[i] = 0; ---> [0, 0, 0, 0, 0, 0, 0, 0] i = 0; k = 0; result[0] = result[0] + Val[0]*d[Col[0]]; result[0] = result[0] + Val[0]*d[0]; result[0] = 0 + 11*1; ---> [11, 0, 0, 0, 0, 0, 0, 0] i = 0; k = 1; result[0] = result[0] + Val[1]*d[Col[1]]; result[0] = result[0] + Val[1]*d[1]; result[0] = 0 + 12*0; ---> [11, 0, 0, 0, 0, 0, 0, 0] i = 0; k = 2; result[0] = result[0] + Val[2]*d[Col[2]]; result[0] = result[0] + Val[2]*d[3]; result[0] = 0 + 14*0; ---> [11, 0, 0, 0, 0, 0, 0, 0] ... i = 2; k = RowPtr[2] = 6; result[2] = result[2] + Val[6]*d[Col[6]]; result[2] = result[2] + Val[6]*d[0]; result[2] = 0 + 31*1; ---> [11, 0, 31, 0, 0, 0, 0, 0] - Advantage of CSR method over Coordinate-wise method:
- The number of operations to perform matrix-vector
multiplication in both storage method are the same...
- However: the number of memory accesses is reduced
(by 2 to be exact) in the CSR method:
- The statement
-
result[Row[k]] = result[Row[k]] + Val[k]*d[Col[k]];
in the Coordinate-wise method, uses 2 more memory accesses than the statement
-
result[i] = result[i] + Val[k]*d[Col[k]];
in the CSR method.
- The number of operations to perform matrix-vector
multiplication in both storage method are the same...