---

Designing a recursive "insert at tail of list" algorithm

---

• The List structure used in the "insert at tail of list" algorithm
  • To make the material more concrete, I will use this List structure to illustrate the "insert at tail of list" algorithm on linked lists:

    public class List { int value; List next; // This is a "reference" (= address) variable !! }

    A List object has the following structure:

    The offset of the field value from the base address is 0
    The offset of the field next from the base address is 4

  Sample list:

  ---

  ---

  ---

  ---

• Inserting a (new) list element at the tail of a list
  • Problem description:

    Given a linked list (with list element of the above structure) pointed to by the variable head Given a new list element (with the above structure) pointed to by the variable ptr Write a recursive function List Insert(List h, List ptr) that: Inserts the new list element at ptr as the last element in the list staring at h Return the reference of the first element of the new list that contain the newly inserted element.

    Example:

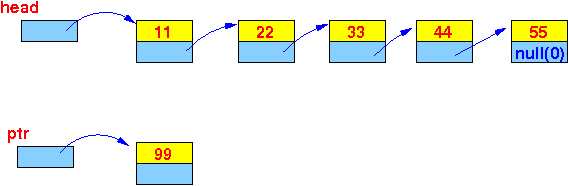
    If we call Insert(head, ptr) where head and ptr are as follows: The Insert(head, ptr) call will construct the following list: And return the pointer to the first element:

    ---

    ---

  • Now we will develop the recursive function List Insert(List h, List ptr)

    To understand how you can come up with a recursive algorithm, you must again use the recursive nature of a linked list:

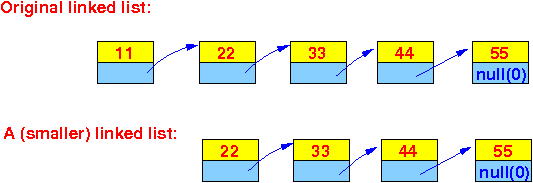
    Due to the recusive nature of a linked list, we can use divide and conquer to solve the original problem using the solution of a smaller problem:

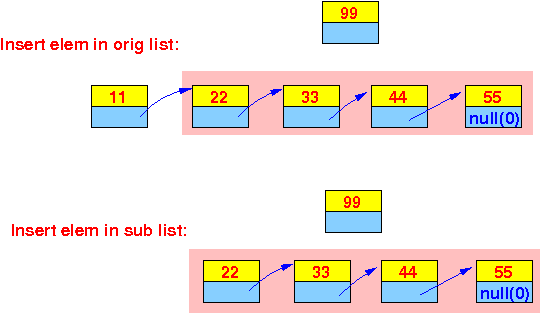
    (You should recognize that inserting a list element in the original list and inserting a list element in the sub-list is the same kind of problem and can be solved with the same algorithm !!!)

    When we write the recursive "insert at the tail" algorithm:

    List Insert( List h, List ptr ) { // We are developing this algorith right now... }

    The input parameter h will represent the original list and the input parameter ptr will represent the insert list element

    ---

    ---

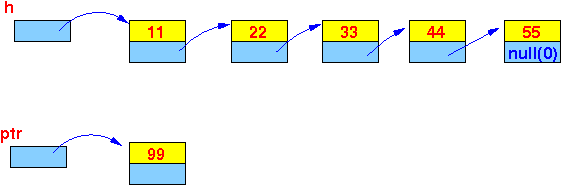
  • In order to insert the list element ptr in the list starting at h, we must find the last element in the list (and insert behind it).

    So the Lookup( ) method will be like this:

    List Insert( List h, List ptr ) { if ( list h is empty ) { return the list with element ptr; } else if ( first element is the last element ) { (1) insert ptr after the first element (2) return h } else if ( 2nd element is the last element ) { (1) insert ptr after the 2nd element (2) return h } else if ( 3rd element is the last element ) { (1) insert ptr after the 3rd element (2) return h } and so on.... }

    Notice that the work done in the highlighted area is the task:

    Insert the element ptr at the tail of this sub-list of the original list:

    So we can replace this code using a Insert( ) call to insert in that sublist:

    List Insert( List h, List ptr ) { if ( list h is empty ) { return the list with element ptr; } else if ( first element is the last element ) { (1) insert ptr after the first element (2) return h } else return Insert( h.next, ptr ); }

  ---

  ---

  ---

  ---

• The recursive Lookup algorithm
  • Using the design above, we can now flesh out the recursive Lookup( ) algorithm in Java syntax:

    (You just need to use Java expressions to replace the pseudo code in the description)

    The Lookup method in Java (without the class, we can add that later) is:

    static int Lookup( List h, int searchKey ) { if ( h == null ) return 0; // Not found is represented by 0 else if ( h.key == searchKey ) return (h.value); else return Lookup( h.next, searchKey ); }

    In CS170 or CS171, you would have learn that the cases h == null and h.key == searchKey are called the base cases.

    I hope with this approach, you get a feel on how the recursion was introduced:

    We first solve the problem without recursion Then we recognize that all the work done by some part of the algorithm is the same as the solution of a smaller problem We replace that part with a recursive call The remaining part that are not covered will become the bases cases.

    ---

  • Example Program: (Demo above code)                                                
    • Prog file: /home/cs255001/demo/asm/9-list-recurison/Lookup.java

    How to run the program:

    To compile:   javac Lookup.java          To run: java Lookup