The general algorithm to convert an
int (2s compl) repr
to a number string
Explained using input number -123:
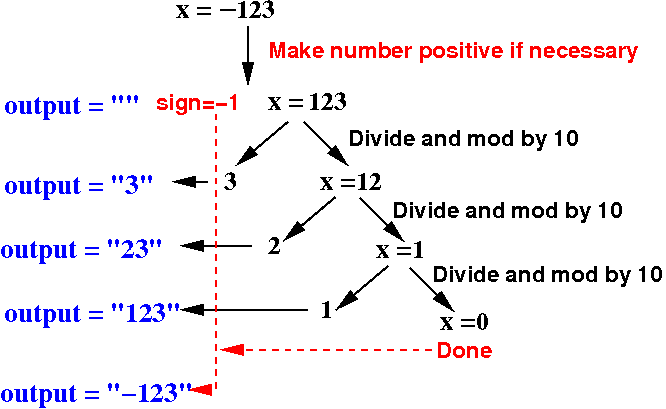
The general algorithm to convert an
int (2s compl) repr
to a number string
Input: x = 11111111111111111111111111110100 (= -12(10))
(1) if ( x < 0 )
sign = -1; x = -x;
else
sign = 0;
sign = -1, x = 00000000000000000000000000001100
(2) while ( x != 0 )
{ Divide the input repeatedly by 10 (in binary arithmetic)
Prepend remainder of division to output
}
00001100 / 00001010: Quotient = 00000001 Rem = 00000010
00000001 / 00001010: Quotient = 00000000 Rem = 00000001
(3) Map each remainder to the corresponding ASCII code with:
ASCII code = digit + 48
We get the ASCII codes: 50 ('2') 49 ('1')
(4) Concatenate the ASCII codes into a string
starting from the last remainder to the first remainder
(5) if ( sign == -1 )
prepend output with "-"
|
Algorithm to convert a
2s compl representation
into
integer number string
The conversion algorithm in Java:
/* ---
myToString(): Integer to Ascii conversion function
--- */
public static String myToString(int input)
{
boolean inputWasNeg;
int remainder[] = new int[100];
char digit[] = new char[100]; // Max 100 digits in number
String result;
int nDigits;
/* ---------------------------------------
Handle SPECIAL case
--------------------------------------- */
if (input == 0)
{
return "0"; // The algorithm does not handle input == 0
}
/* ---------------------------------------
Check if input is negative
--------------------------------------- */
if (input < 0)
{
inputWasNeg = true;
input = -input; // Negate to make input positive
}
else
{
inputWasNeg = false;
}
/* -------------------------------------------------------
Get all digit by collecting remainders divided by 10
------------------------------------------------------- */
nDigits = 0; // Count # digits in number
while (input > 0)
{
remainder[nDigits] = input % 10;
nDigits++;
input = input / 10;
}
/* ---------------------------------------------------------
Convert "digits" to character (ASCII code) using:
ASCII code = digit + 48
--------------------------------------------------------- */
for (int i = 0; i < nDigits; i++)
{
digit[i] = (char) (remainder[i] + 48); // Or use '0' for 48
}
/* ---------------------------------------------------------
Make a string (start with last remainder)
--------------------------------------------------------- */
result = ""; // Initialize output string
for (int i = nDigits-1; i >= 0; i--)
result = result + digit[i]; // Add next digit
/* ---------------------------------------------------------
Prepend '-' if input was negative
--------------------------------------------------------- */
if ( inputWasNeg == true )
{
result = "-" + result; // Try: "******" + result for banks
}
return(result);
}
DEMO: /home/cs255001/demo/atoi/Itoa.java
Application: the
System.out.println( )
method in Java
|