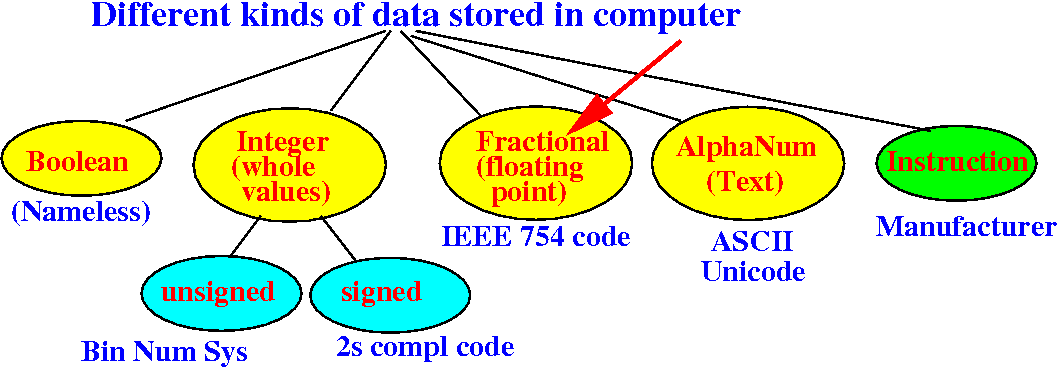
Overview: the different kinds of data stored in a computer
 

 

We will study how fractional numbers are represented inside a computer next

Fixed point decimal numbers
 

I will use fixed point decimal numbers to introduce ("ease into") the fixed point binary numbers

  • Decimal point = a point (period) places in a number representation to mark the location of the digit whose weight = 1

  • The weight of digits moving towards left increases by a factor of 10

  • The weight of digits moving towards right decreases by a factor of 10

Fixed point decimal numbers
 

Example: 

  Decimal number:     123.45
                      ^^^ ^^
                      ||| ||
                      ||| |+---  weight = 1/100   
                      ||| +----  weight = 1/10
                      ||+------- weight = 1
                      |+-------- weight = 10
                      +--------- weight = 100

Fixed point binary numbers
 

Structure of a fixed point binary number:

  • Binary decimal point = a point (period) places in a binary number representation to indicate the location of the digit whose weight = 1

  • The weight of digits moving towards left increases by a factor of 2

  • The weight of digits moving towards right decreases by a factor of 2

Fixed point binary numbers
 

Example: 

   Binary number:     101.01
                      ^^^ ^^
                      ||| ||
                      ||| |+---  weight = 1/4    
                      ||| +----  weight = 1/2
                      ||+------- weight = 1
                      |+-------- weight = 2
                      +--------- weight = 4

How to convert fixed point binary repr to fixed point decimal repr
 

Method:   compute the value using decimal arithmetic

Example: 

   Binary number:     101.01
                      ^^^ ^^
                      ||| ||
                      ||| |+---  weight = 1/4    
                      ||| +----  weight = 1/2
                      ||+------- weight = 1
                      |+-------- weight = 2
                      +--------- weight = 4

  The value represented by   101.01(2)  is:

    1*(4) + 0*(2) + 1*(1) + 0*(1/2) + 1*(1/4) = 5 1/4
                                              = 5.25(10)

How to convert fixed point decimal repr to fixed point binary repr

Method:

  • Split the fixed point deciaml representation into 2 parts:

      • An integral part
      • A fractional part      

  • Find the binary representation of the integral part by repeatedly divide the value by 2 (to obtain the powers of 2n)
    Collect the remainders of the divisions in reverse order

  • Find the binary representation of the fractional part by repeatedly multiply the value by 2 (to obtain the powers of 2-n)
    Collect the whole digits of the multiplications in "straight" order

It's easier to understand the method using an example (next slide)

Example: How to convert fixed point decimal repr to fixed point binary repr

Convert 23.6875(10) to fixed point binary representation:

  • Split 23.6875 into 2 parts:

      • Integral part = 23
      • Fractional part = 0.6875      

  • Convert integral part (= 23) by repeatly dividing by 2
    Collect the remainders in reverse: 10111

  • Convert fractional part (0.6875) by repeatly multiplying by 2
    Collect the "whole" digits in order: 0.1011

  • Concatenate the 2 pieces with a decimal point between them: 10111.1011

(Worked on on next slide)

I will do this example in the lecture (using paint as writing board)

Worked out example

  • Converting 23.6875(10) into fixed point binary representation: 

       23.6875 ------>     23          0.6875


   Convert integer part           Convert fractional part
  =======================        =========================

        23                            0.6875
     2 ----- 1    ^               x2 --------- 1     |
        11        |                   1.3750         |
     2 ----- 1    |               x2 --------- 0     |
         5        |                   0.750          |
     2 ----- 1    |               x2 --------- 1     |
         2        |                   1.5            |
     2 ----- 0	  |               x2 --------- 1     V
         1        |                   1.0   <--- stop
     2 ----- 1    |            
         0

        10111                                0.1011


 Therefore:

       23.6875(10) = 10111.1011(2)

Postscript
 

Comments:

  • Computers do not use fixed point (binary) representation

    Instead, computers use floating point (binary) representation

  • We discussed the fixed point (binary) representation as a pre-requisite for understanding the floating point (binary) representation (which will be discussed next)