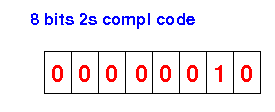
The 2s complement code:
|
The 2s complement code is based on modular arithmetic....
Overview:
|
The 8 bits 2s complement code is a mapping between any 8 bits number and its signed value:
3 digit number Signed value
-------------- --------------
0000000 <---> ...
0000001 <---> ...
1111111 <---> ...
|
The mapping must has desirable computational properties !!
We can achieve these desriable computation properties using "wrap-around" arithmetic in binary - just like the 10s compl code
Suppose we have a binary number odometer that is very special:
|
Question:
|
Question:
|
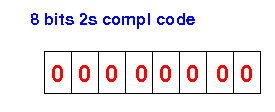
Answer: 11111111 + 1 = 00000000 (because the odometer has 8 bits and cannot display 9 bits)
|
Question:
|
Question:
|
Answer: 00000000 − 1 = 11111111 !!!

|
8 bits can represent 28 = 256 different values
Here is the mapping between 8 bits 2s compl code and the signed values between [−128, 127]:
2s comp Intrinsic Decimal Code value sign-magnitude repr ==================================================== 10000000 -128 <--- largest negative value using 8 bits (−27) 10000001 -127 ..... .... .... 11111000 •••••••• -8 11111001 ••••••• -7 11111010 •••••• -6 11111011 ••••• -5 11111100 •••• -4 11111101 ••• -3 11111110 •• -2 11111111 • -1 00000000 ( ) 0 00000001 • 1 00000010 •• 2 00000011 ••• 3 00000100 •••• 4 00000101 ••••• 5 00000110 •••••• 6 00000111 ••••••• 7 00001000 •••••••• 8 ..... .... .... 01111111 127 <--- largest positive value using 8 bits (27-1) |
The mapping is based on modular addition and subtraction that you can see if we show the mapping on a circle:

Program that shows the 2s complement code and their sign-magnitude representations:
|
Background info:
|
Try these inputs:
a = 2, b = 1 a = 2, b = -1 (adding neg value works - i.e.: without subtraction !) a = -1, b = 2 a = 127, b = 1 (overflow !) |
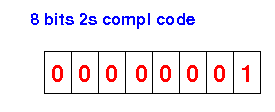 forward 1 mile:
forward 1 mile: