The signed decimal code (or representation): (a sign-magnitude code)

   Signed decimal code        Represented signed value   
         ...                           ...
         -2                            ••
         -1                            •
          0                           
          1                            •
          2                            ••
        ...                            ...
   

Short-coming:   the meaning of +/- operations depends on values of the operands

       2  The + operation depends on the values 
   +  -1  of its operands
 --------
       1  (To obtain 1, we subtracted 2 and 1)
   

The 3 digit 10s complement code (or representation): (a sign-magnitude code)

   3 digit 10s compl code     Represented signed value 
         ...                        ...
         998                        ••
         999                        •
         000                       
         001                        •
         002                        ••
         ...                        ...
   

Advantage:   when we compute 2 + −1 using the 3 digit 10s compl representation:

     002  The + operation is independent from the values 
   + 999  of its operands
 --------
     001  (To obtain the result, we added 002 and 999)
   

The 3 digit 10s complement code (or representation): (a sign-magnitude code)

   3 digit 10s compl code     Represented signed value 
         ...                        ...
         998                        ••
         999                        •
         000                       
         001                        •
         002                        ••
         ...                        ...
   

Subtraction works equally well:   3 − 4 = −1 is computed in 10s complement as follows:

       003   (We can always borrow from a digit to the left)
     - 004
    -------
       999     (999 represents the value -1)

Due to the limitation to only 3 digits, the signed values are mapped by the 3 digit 10s compl code on a circle:

Adding 1 to a 3 digit 10s compl code is moving clock-wise 1 position on the circle:

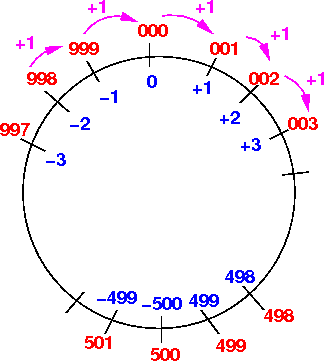
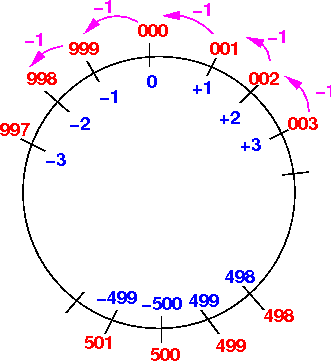
Subtracting 1 from a 3 digit 10s compl code is moving anti-clock-wise 1 position on the circle:

Suppose we compute:   2 + (−1) = 1 --- (note: + means: move forward (clock-wise))

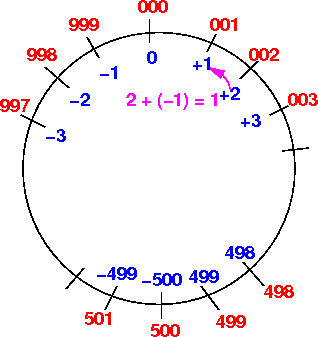
How many positions forwards (= clock-wise) do we have to move to reach the position 001 on the circle ???

When we compute 2 + (−1) = 1 - we can move forward from 002 to 001 as follows:

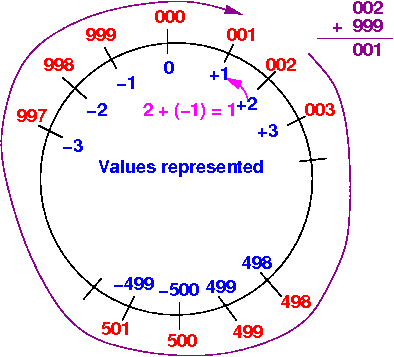
We can move from 002 to 001 by going clock-wise 999 positions !!!

Therefore:   by representing NEGATIVE ONE as 999, we will keep the meaning of + operation independent from the value of the operands !!!

BTW: truncating the carry digit in an addition is basically modular arithmetic