Prelude to the 2s complement code: the 10s complement code

Our objective:
Discuss how signed values are represented by the 2s complement code in computers to

We will first study:

The 10s complement code

Reasons:

The coding technique used in 10s complement code is similar to the 2s complement code
The 10s complement code uses decimal arithmentic while the 2s complement code uses binary arithmetic
Humans are more skilled in decimal arithmetic (so it's easier to understand)

Review of codes

Recall: there are 2 types of codes:

"Committee-based"/"Agreement" code
Example:
The meaning of each code word in the code is agreed upon
Mathematical codes
Example:
The meaning of a code word is computed
Example: the meaning of 00000101₍₂₎ is computed using the formula 0×2⁷ + 0×2⁶ + 0×2⁵ + 0×2⁴ + 0×2³ + 1×2² + 0×2¹ + 1×2⁰

The 10s complement code is a Mathematical code

Intro to the 10s complement code

The 10s complement code is based on modular arithmetic....
But, I will not use modular arithmetic
Instead, I will explain the 10s complement code using a (modified) car's odometer (easier to understand):

Overview:

The 10s complement code uses a fixed number of (decimal) digits
Each decimal number of the 10s complement code is mapped to a signed value

How I will explain the 10s complement code

Note:

There are many different 10s complement (or odometer) codes:

10s complement code of 1 digit
10s complement code of 2 digits
10s complement code of 3 digits
10s complement code of 4 digits
And so on...

I will use a 3 (decimal) digits code to explain the 10s complement code:

10s complement codes using different number of digit will work in a similar manner

What is a 3 digits 10s complement code ?

The 3 digits 10s complement code is a mapping between any 3 digits number and a signed value:

All possible Corresponding 3 digit number Signed value -------------- -------------- 000 <---> ... 001 <---> ... ... ... ... ... 999 <---> ...

Warning: this mapping will not be a mapping you are "used to"...

This mapping will provide some desirable computational properties !!

I will explain how to obtain the mapping using a "special" odometer - discussed next

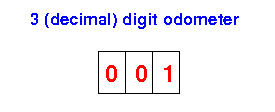
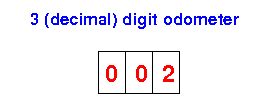
The mapping is based on the behvavior of the car's odometer

Imagine that the odometer of a car operates in the following manner:

When the car goes forward, its odometer will increase by 1 after driving 1 mile
forward 1 mile:
When the car goes backwards (i.e.: drive in reverse), its odometer will decrease by 1 after driving 1 mile
reverse 1 mile:

$64,000 question

Question:

Starting with odometer reading 999:

we drive forward (= add) 1 mile.
What's the new odometer reading ?

$64,000 question

Question:

Starting with odometer reading 999:

we drive forward (= add) 1 mile.
What's the new odometer reading ?

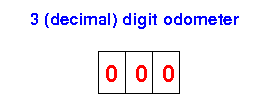
Answer: 999 + 1 = 000 (because the odometer has 3 digits)

Note: the carry is lost because the odometer only has 3 digits !

$64,000 question

Question:

Starting with odometer reading 000:

we drive in reverse (= subtract) 1 mile.
What's the new odometer reading ?

$64,000 question

Question:

Starting with odometer reading 000:

we drive in reverse (= subtract) 1 mile.
What's the new odometer reading ?

Answer: 000 − 1 = 999 !!!

We will use this property to map the negative values !!!

What is a 10s complement code (in general)

The 3 digit 10s complement code is a (Mathematical) mapping between all 3 digit number and some set of signed value:

3 digits 10s complement code 3 digit number Signed value -------------- -------------- 000 <---> ... 001 <---> ... (A subset of signed values) 999 <---> ...

This mapping provides a very attractive property

In the next set of slides, we will define this mapping in a piece meal fashion by driving the car and observing the odometer reading

After that, I'll show you the "atractive property" of using the 10s complement code in arithmetic operations