|
|
|
|
See how the Euclid's Algorithm works with an example:

Find the Greatest Common Divisor of A=28 and B=36 |
Let's execute the Euclid's Algorithm ourselves (you are pretending to be a computer !)

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A)
}
|
We will execute this step:

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A) <------
}
|
Result:

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A)
}
|
Question: what will the algorithm do next ?
We will execute this step:

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B) <------
otherwise
replace B with the value (B - A)
}
|
Result:
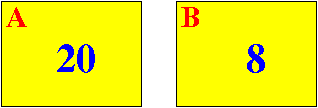
Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A)
}
|
Question: what will the algorithm do next ?
We will execute this step:

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B) <------
otherwise
replace B with the value (B - A)
}
|
Result:
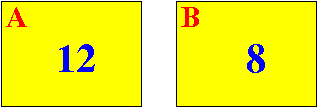
Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A)
}
|
Question: what will the algorithm do next ?
We will execute this step:

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B) <------
otherwise
replace B with the value (B - A)
}
|
Result:
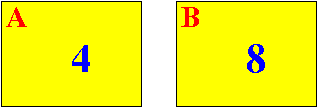
Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A)
}
|
Question: what will the algorithm do next ?
We will execute this step:

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A) <------
}
|
Result:
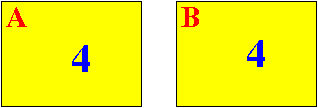
Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A)
}
|
Question: what will the algorithm do next ?
We will execute this step:

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A) <------
}
|
Result:

Step 1 of Euclid's Algorithm:
As long as neither number is equal to zero (0) do
{
if ( A > B )
replace A with the value (A - B)
otherwise
replace B with the value (B - A)
}
|
Question: what will the algorithm do next ?
Step 1 ends and we continue to step 2:

Step 2 of Euclid's Algorithm:
if ( A > 0 )
The Greatest Common Divisor is A
otherwise
The Greatest Common Divisor is B
|
Question: what will the algorithm do next ?
Result:

Step 2 of Euclid's Algorithm:
if ( A > 0 )
The Greatest Common Divisor is A <----
otherwise
The Greatest Common Divisor is B
|
Result: the greatest common divisor of 28 and 36 is 4