---

An amortization performance analysis of the Splay Tree

---

• Performance analysis in general
  • Before you can study the performance of an operation you need to know exactly what that operation is doing....

  ---

  ---

• Work done in lookup, insert and delete
  • Lookup (get(k)):

    Traverse tree to find k: Splay node k:

    ---

  • Insert (put(k,v)):

    Find location in tree to insert k: Splay node k:

    ---

  • Delete (remove(k)):

    Traverse tree to find k to delete: Splay the parent node of node k:

    ---

  • Now we need to count operations:

    A zig/zag operation is more "costly" than traverse one link We can ignore the cost to traverse the tree to find the key k

    ---

  • Question:

    What is the cost of these operations:            Zig-zig           Zig-zag Zig

  ---

  ---

• Classic tree-rotation operations
  • Right-rotation:

    ---

  • Left-rotation:

  ---

  ---

• A Zig-zig operation = 2 tree rotation operations
  • Zig-zig (1):

    The zig-zig (1) operation: Zig-zig(1) = right-right

    ---

  • The zig-zig (2) operation:

    Zig-zig(2) = left-left (It's similar to zig-zig(1))

  ---

  ---

• A Zig-zag operation = 2 tree rotation operations
  • Zig-zag (1):

    The zig-zag (1) operation: Zig-zig(1) = right-left

    ---

  • The zig-zag (2) operation:

    Zig-zig(2) = left-right (It's similar to zig-zag(1))

  ---

  ---

• A Zig operation = 1 tree rotation operations
  • Zig (1):

    The zig (1) operation: Zig (1) = left

    ---

  • The zig (2) operation:

    Zig (2) = right (It's similar to zig (1))

  ---

  ---

  ---

  ---

• Number of Tree-rotation operations to splay a node
  • Recall:

    The zig-zig operation moves a node x up 2 levels The zig-zag operation alos moves a node x up 2 levels         The zig operation moves a node x up 1 level

    ---

  • The cost to splay a node x at depth d (i.e., to make node x the new root node):

    To splay a node x at depth d (d = even), we need: d/2      zig-zig and/or zig-zag operations    = d   tree-rotation operations To splay a node x at depth d (d = even), we need: (d−1)/2      zig-zig and/or zig-zag operations        1                 zig operation    = d   tree-rotation operations

    ---

  • Conclusion:

    Cost to splay node x at depth d = d tree rotation operations

  ---

  ---

  ---

  ---

• Definitions and Notations
  • Notations:

    T = the splay tree with n nodes v = a node in T n(v) = number of nodes in the subtree rooted at v       r(v) = 2log(n(v))      (the rank of node v) root = the root node of the splay tree T n(root) = 2×n + 1 r(root) = 2log(2×n + 1)   ~=   2log(2×n)   =   2log(n) + 1        Example: Let e = a leaf node in T n(e) = 1 r(e) = 2log(1) = 0

  ---

  ---

  ---

  ---

• An amortization scheme to analyze the average performance of the Splay operation
  • Prelude:

    Please don't ask how did they come up with this amortization scheme It's black magic :-) All I will do is show you that it work...

    ---

    ---

  • Recall that the cost to splay a node with depth = d:

    c(splay node v at depth d) = d (tree rotation operations)

  • Recall also that in an amortization analysis, we spread the cost by:

    Saving an additional (extra) tree rotation operations per splay tree operations (insert, delete, lookup) And we must make sure that the additional (extra) tree rotation operations saved will never become negative (i.e., have enough)

    ---

    ---

  • Black magic: The balance (extra amount) of tree-rotation operations that you need to keep (save) in a node v of the splay tree is:

    Bal(v) = r(v)

    Note:

    This is what I refered to as black magic How did they come up with this number ???

    ---

  • Example: balance of tree-rotation operations kept in node in a splay tree

  ---

  ---

  ---

  ---

• Definition: r(T) = Total balance of extra operations in tree T
  • Definition:

    r(T) = Total # extra tree operations stored in tree T

    Example:

    r(T) = lg(15) + lg(11) + 2lg(5) + 3lg(3)

  ---

  ---

  ---

  ---

• How the balance "Bal(v)" changes when you splay a node
  • Example: splay tree before and after splay(node 3)

    Notes:

    Before splay(3): r(T) = lg(15) + lg(11) + 2lg(5) + 3lg(3) After splay(3): r'(T) = lg(15) + lg(11) + lg(9) + lg(5) + 3lg(3) Change in balance: &Delta(r(T)) = r'(T) - r(T) = lg(9) - lg(5)

  ---

  ---

• The amortized cost of a splay operation
  • We amortize the cost of a splay operation on a node x at depth d as follows:

    "Pay" d tree rotation operations (= the real cost to splay the node x at depth d) "Tag on" this extra number of operations: &Delta(r(T))

    ---

  • The amortized cost to splay a node x at depth d:

    Amortized cost of splay(x) = d + &Delta(r(T))                   ....... (1)

    ---

  • Claim:

    The total balance r(T) of any tree T resulting from a splay operation satisfies: r(T) ≥ 0

    (This is trivial because we added in the difference so the total will never become negative...)

    ---

    ---

  • $64,000 question:

    What is the order of d + Δ(r(T)) ???

    To answer this question, we must look at the amortized cost of a tree rotation operation

    Because: splay(x) = d tree rotations....

  ---

  ---

  ---

  ---

  ---

  ---

• The amortized cost of a tree-rotation operation
  • Consider the right rotation operation:

    ---

  • Bigger picture:

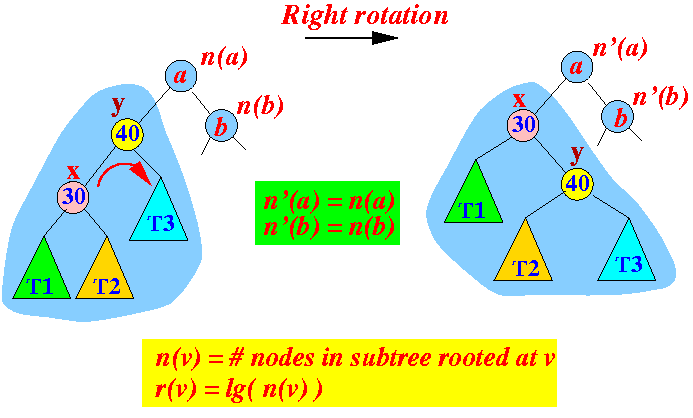
    Notice that:

    The tree rotation does not change the number of nodes in the right (other) sub tree rooted at a       Therefore: n'(v) = n(v)        for each node v in the right subtree of a

    Notice also that:

    The number of nodes in the subtrees T1, T2 and T3 are unchanged Therefore: n'(v) = n(v)        for each node v in the subtress T1, T2 and T3

    Conclusion:

    The only changes in the n(v) values are at nodes v = x and v = y

    ---

    ---

  • The change in r(v) of nodes x and y are as follows:

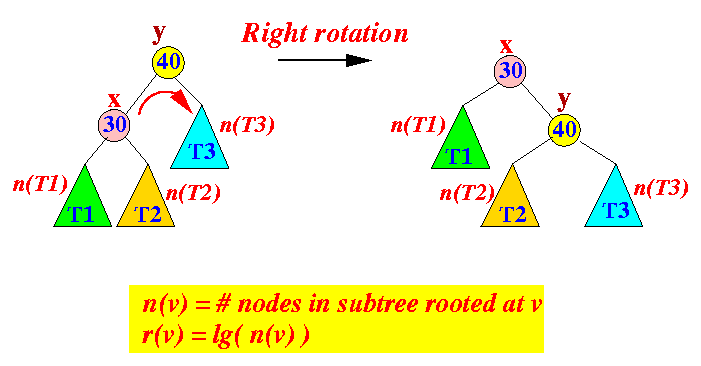
    Notes:

    Before the rotation: n(x) = n(T1) + n(T2) + 1 n(y) = n(T1) + n(T2) + n(T3) + 2 After the rotation: n'(x) = n(T1) + n(T2) + n(T3) + 2 n'(y) = n(T2) + n(T3) + 1

    ---

    ---

  • Total change in balance stored in tree:

    Δ(r(T)) = r'(T) - r(T) = ( r'(1) + r'(2) + .... + r'(x) + r'(y) + .... + r'(n) ) - ( r(1) + r(2) + .... + r(x) + r(y) + .... + r(n) ) = ( r'(x) + r'(y) ) - ( r(x) + r(y) ) n(y) = n(T1) + n(T2) + n(T3) + 2 n'(x) = n(T1) + n(T2) + n(T3) + 2 ==> r'(x) = r(y) Δ(r(T)) = r'(y) - r(x) From: We have that: n'(x) > n'(y) ==> r'(x) > r'(y) Therefore: Δ(r(T)) = r'(y) - r(x) < r'(x) - r(x)

  ---

  ---

  ---

  ---

• The change in balance caused by a splay operation
  • We can compute the change of balance caused by a splay(x) operation by:

    repeated execute tree-rotation on node x until it becomes the root node

    Example:

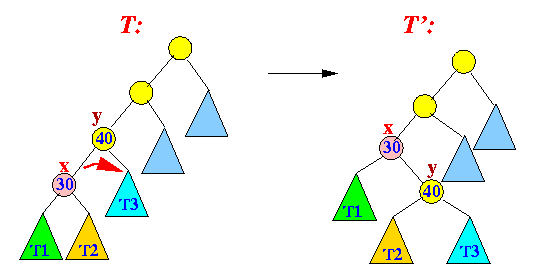
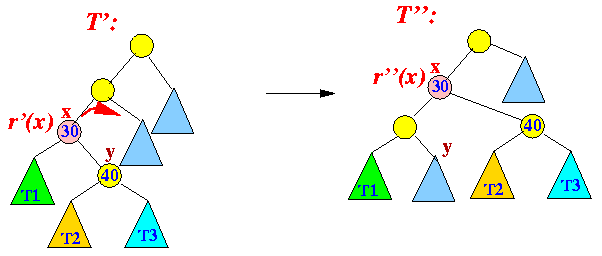
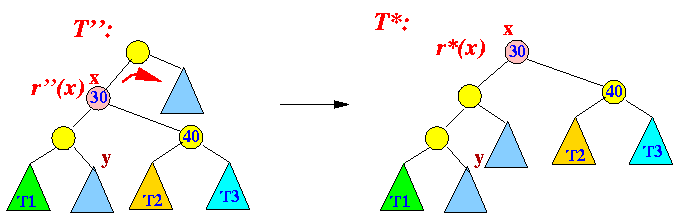
    Tree rotate on x: r(T') - r(T)  <  r'(x) - r(x) Tree rotate on x again: r(T') - r(T)  <  r''(x) - r'(x) And so on.... Until x is the root node: r(T*) - r(T'')  <  r*(x) - r''(x)

    ---

  • Balance change caused by the splay(x) operation:

    r( final tree ) - r( starting tree ) = r(T*) - r(T) = r(T*) - r''''''''(T) + ..... (all intermedtiate trees) + r''''(T) - r'''(T) + r'''(T) - r''(T) + r''(T) - r'(T) + r'(T) - r(T) < r*(x) - r''''''''(x) + .... + r''''(x) - r'''(x) + r'''(x) - r''(x) + r''(x) - r'(x) + r'(x) - r(x) (all but 2 terms cancel each other) = r*(x) - r(x) r*(x) = r(root node) (because x is the new root in the final tree) = lg( # nodes in splay tree ) = lg(n)