- Definitions:
- h =
the height of an
AVL tree
- n(h) = the minimum number of nodes in an AVL tree of height h
- h =
the height of an
AVL tree
- Some facts on n(h):
- n(1) = 1 and
n(2) = 2:
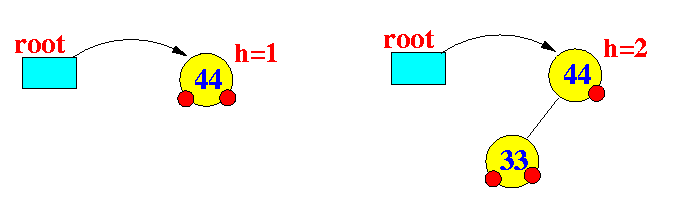
- n(1) = 1 and
n(2) = 2:
- Consider the minimum number
of nodes in
an AVL tree of
height h:

Note:
- In order to put the minimum
number of nodes
in an AVL tree of
height h,
we must:
- put the minimum number of nodes in its 2 sub trees
- Because the maximum difference in height
is 1 (one),
the minimum sub trees
are as follows:
- One of the sub tree has
height h−1
(in order to make the height
of the original tree = h)
- The other sub tree has
height h−2
(to minimize the # nodes
in the AVL tree)
- Both sub trees
have the minimum number of nodes
Therefore:
- Sub tree 1 has n(h−1) nodes
- Sub tree 2 has n(h−2) nodes
- One of the sub tree has
height h−1
(in order to make the height
of the original tree = h)
- In order to put the minimum
number of nodes
in an AVL tree of
height h,
we must:
- Relationship between n(h), n(h−1) and n(h−2):
n(h) = 1 + n(h−1) + n(h−2) ...... (1) n(1) = 1 n(2) = 2
- We use Mathematica to solve this
recurrence equation:
math In[0]:= RSolve[ {n[h]==1+n[h-1]+n[h-2], n[0]==1, n[1]==2}, n[h], h ] Out[0]= {{n[h] -> -1 + 2 Fibonacci[h] + LucasL[h]}} Which is equals to: / 1/2 \ / 1/2\h / 1/2 \ / 1/2\h |3 5 | | 5 | | 3 5 | | 5 | |------ + 1/2| |1/2 + ----| + |- ------ + 1/2| |1/2 - ----| - 1 \ 10 / \ 2 / \ 10 / \ 2 / 1/2 / 2 \h 1/2 / 2 \h 2 5 |- --------| 2 5 |- --------| | 1/2| | 1/2| \ 1 - 5 / \ 1 + 5 / - -------------------- + -------------------- 1/2 1/2 5 (1 - 5 ) 5 (1 + 5 ) approximately equal to ~= 2 × 1.6hExample:
> -1 + 2 Fibonacci[5] + LucasL[5] 20 > 2*1.6^5 20.9715
> -1 + 2 Fibonacci[10] + LucasL[10] 232 > 2*1.6^10 219.902
> -1 + 2 Fibonacci[15] + LucasL[15] 2583 > 2*1.6^15 2305.84
- From above, we found:
n(h) = minimum number of nodes in an AVL tree of height h ~= 2 × 1.6h ....... (2)
- Notation:
- m(h) = number of nodes in an AVL tree of height h
- We have that:
m(h) > min. # nodes in AVL tree of height h > n(h) > 2 × 1.6h
Reverse the inequality: 2 × 1.6h < m(h) <==> 1.6h < m(h)/2 <==> log(1.6h) < log(m(h)/2) <==> h log(1.6) < log(m(h)) - 1 <==> 0.678 h < log(m(h)) - 1 <==> h < 1.475 log(m(h)) - 1.475 ...... (3) ==> h < 2 log(m(h)) + 2 (in text book)
- Therefore (acording to Goodrich):
- The height of an AVL tree that contains m entries is < 2 log(m) + 2
(This was a rough estimate, I gave you a more accurate estimate above)
- Some maximum heights:
- m = 100, h < 15.28
- m = 1000, h < 21.93
- m = 10000, h < 28.57
- Running time of lookup:
- O(log(n)) (n = # entries)