Deleting an entry from the (2,4)-tree

Preliminary to deleting

Prelim:

Preliminary Delete procedure:

Entry remove(Key k) { e = keySearch(k, root); // Find entry containing key k // starting with the root node if ( e == null ) return; // Not found, exit... Delete the entry e from the node that contains e. }

The rest of this webpage will discuss how to:

Deleting an entry from a leaf node with ≥ 2 entries
- The easiest delete operation is:
- How to delete an entry e in this case:
- Example:
Simplified node representaion
- I have to draw larger 2,4-trees and there is not enough space to display the entire node....
- Due to space limitation, I will use a simplified way to represent nodes in the (2,4)-tree:

Deleting an entry from a non-leaf node

The delete procedure for an entry stored in a non-leaf node is similar to the one used in Binary Search Trees:

Delete the entry from the non-leaf node...
Then:

Note:

The successor/predecessor entry will always be stored inside a leaf node !!!)
Therefore:

Example:

delete entry with key = 12:
Delete the entry:
Replace the deleted entry with its successor (or predecessor):

How to find the successor and predecessor entry

How to find the successor of some entry:

Where is the successor entry:
Example:
Procedure: (just like the one used in the Binary Search Tree)

How to find the predecessor of some entry:

Where is the successor entry:
Example:
Procedure: (just like the one used in the Binary Search Tree)

Repeated example of deletion now with successor location algorithm:

Delete key 12 from this tree:
First, delete the key 12 from the node (do not reshuffle the remaining keys within the node):
Find the successor entry....
Then, replace the deleted entry with its successor entry (or its predecessor)

Important lesson learned

Important fact:

The deletion an entry from an node with internal children node (i.e, from a non-leaf node) will eventually result in:

(This is exactly like a delete operation in a binary search tree)

Note:

Deleting an entry from a node with exactly 1 entry --- i.e., deleting the last entry in a node

Deleting an entry e from a node p with exactly 1 entry:

There are 2 methods used to handle underflow:

Transfer one entry from an immediate sibling node (and the parent node) into the underflow (empty) node
Merge the underflow node (with has 0 entries) with one of the immediate sibling nodes

Detailed procedure for handling an underflow situation in the node p (i.e., node p is now empty):

If one (left or right) immediate sibling node of node has ≥ 2 entries:

Transfer the entry from node p's parent to replace the deleted entry e in node p, and
Transfer an entry from the immediately sibling to node p's parent

If node p's immediate sibling nodes have 1 entry:

Merge:
into one single node

Notice that:

The merge operation will remove an entry from node p's parent node !

Consequently:

Node p's parent node can itself become underflow (= empty) !!!

Solution:

Repeat the same procedure at p's parent node
In other words:
In yet other words:

Clarification: the "immediate" sibling node

Terminology:

Sibling nodes are nodes that share the same parent node
Example:
What I (not in text books) call immediate sibling nodes, are sibling nodes that are next to each other
Example:

How to find the immediate sibling nodes:

The immediate right sibling node of a node p is found at the root of the "next right" subtree of p's parent node
Example:
The immediate left sibling node of a node p is found at the root of the "last left" subtree of p's parent node
Example:

Solving underflow by transfering with a sibling that has ≥ 2 entries

Technique:

If an underflow condition occurs in a delete operation, and one of the immediate sibling nodes has ≥ 2 entries, we can solve the underflow condition by:

Transfer with its right sibling:

Let's start with a delete operation that caused an underflow: remove(6)
Transfer:
Graphically:
Note:

Transfer with its left sibling:

Delete the entry:
Transfer:
Graphically:
Note:

Very important note:

When we transfer a subtree reference into another node, we must:

Example:

We will see later that the delete operation can cause cascaded transfers up the tree.
We may have to perform a transfer where the red reference is a reference to a subtree:
After the transfer operation, the parent node of the subtree has changed:
You must update the parent reference of the root node in the subtree !!!

Solving underflow by merging when both siblings have 1 entry

Technique:

If an underflow condition occurs in a delete operation, and BOTH immediate sibling nodes have 1 entry, we must solve the underflow condition by:

Example:
Transfering an entry form the sibling node will cause an underflow at the sibling node itself !

Solution:

Merge entries from your parent node and your sibling node to create a "new" node
The "new" node will be the root node of the subtree formed from yourself and your sibling node

The merge operation (on node p that contained entry 10):
Result:

The subtree pointer maintenance in the left merge and the right merge operations

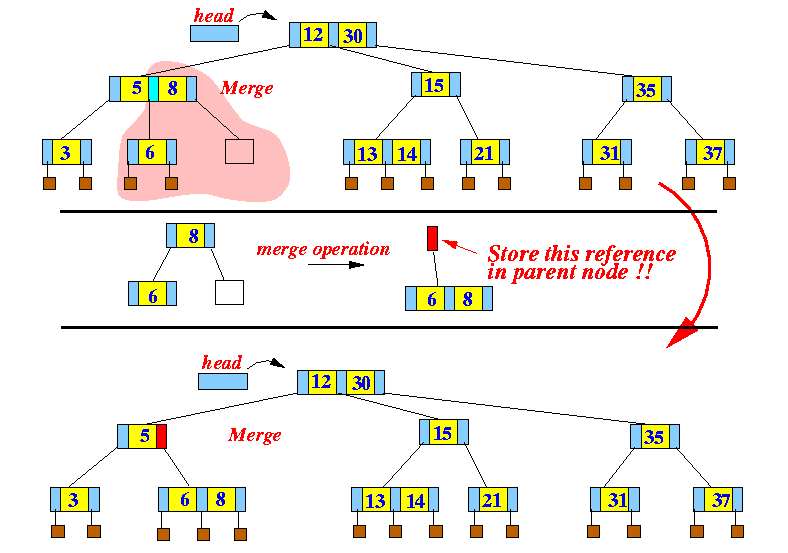
Merging with your left sibling:

Graphically:
The left merge will replace:
by one subtree pointer:

Merging with your right sibling:

Graphically:
The right merge will replace:
by one subtree pointer:

Notice that:

Underflow at the parent node of the delete target node

The merge operation will "remove" one entry from the parent node
Underflow condition at the parent node:
Example:

Handling the underflow condition in the parent node:

Exactly the same method is used:

If node has a immediate sibling with ≥ 2 entries, then:
Note:
If node has a immediate sibling with only 1 entry, then:

Cascaded underflow handled by a transfer operation

Example:

Delete key entry 7:
After the merge operation:
This underflow can be solved with a transfer operation:
Notice that:

Note: transfer with the left sibling

When you perform a transfer operation with your left sibling, you will also transfer the right most subtree link into the sibling node
The right most subtree link will occupy the first slot in the entry
Example:

Cascaded underflow handled by another merge operation

Example:

Notice that:

The second merge operation again "removes" one entry from the grand parent node of the target delete node
The grand parent node can also suffer a underflow condition....
This cascaded underflow/merge sequence will eventually end when an entry is removed from the root node
If the root node has one (1) entry, the removal will can the root node to become empty
An empty root node is discarded
(and the previously merged node becomes the new root !)

Example: underflow at the root node

An example where a deletion causes the root node to underflow (and then removed):

Delete key entry 7:
There is an underflow....
The sibling node has 1 entry ⇒ merge
There is another underflow....
The sibling node has 1 entry ⇒ merge (again)
There is another underflow.... now we reach the root node !!!
The sibling node has 1 entry ⇒ merge (yet again)
The root node has underflowed ⇒ remove it
DONE !!!

The delete algorithm

Psuedo code of remove(k):

Entry remove(Key k) { Entry e; Node p; /* ----------------------- Find k to remove ----------------------- */ e = keySearch(k); /* ======================= Check if k exists... ======================= */ if ( e == null ) { return(null); // Not found, nothing to delete... } /* ------------------------------ Phase 1: remove entry e ------------------------------ */ p = node containing e; if ( p has an internal child node ) { /* ---------------------------- Replace e with e's successor ---------------------------- */ succ = successor entry of the deleted entry e; Swap p.e with succ entry; /* ----------------------------------------------------- The target entry is now in the successor's location ----------------------------------------------------- */ e = succ; p = node containing succ entry; } delete e from p and reshuffle entries in p; // Delete entry // Also: remember the old value /* *********************************************** Handle a possible underflow situation *********************************************** */ if ( p has ≤ 1 entry ) { handleUnderflow(p); // This is a recursive routine ! } return the old value in e; // No underflow; done }

Java code:

public Integer remove(String k) { Entry e; Node p; int pos; /* ----------------------- Find k to remove ----------------------- */ e = keySearch(k); /* ======================= Check if k exists... ======================= */ if ( e == null ) { return(null); // Not found, nothing to delete... } Entry old = e; // Save for return value /* ---------------------------------------------------- Note: searchEndPos = node containing entry e ---------------------------------------------------- */ p = searchEndPos; /* ---------------------------------------------------- Find position of e inside p: p --> | T0 | e0 | T1 | e1 | T2 | e2 | T3 | Which of the e? is e ???? ---------------------------------------------------- */ for ( pos = 0; pos < 3; pos++ ) if ( p.e[pos] == e ) break; /* ---------------------------------------------------- Delete entry e from 2,4-tree ---------------------------------------------------- */ if ( p.child[0] == null /* => leaf node */ ) { /* ================================================== Delete entry e from node Note: this is done by MOVING right most entries into the slot containing e !!! ================================================== */ for ( int i = pos; i < 2; i++ ) p.e[i] = p.e[i+1]; p.e[2] = null; // The right most entry is for sure null ! } else { /* ------------------------------------------------ Non-leaf: replace e with e's successor ------------------------------------------------ */ Node q; /* ------------------------------------------------ Use q to traverse to p's successor ------------------------------------------------ */ System.out.println("pos = " + pos); q = p.child[pos+1]; // Go right while ( q.child[0] != null ) q = q.child[0]; // Go left all the way down. /* ------------------------------------------------ Delete e ------------------------------------------------ */ System.out.println("Replace " + p.e[pos] + " with: " + q.e[0]); p.e[pos] = q.e[0]; // Replace e by e's successor for ( int i = 0; i < 2; i++ ) // Delete e's successor in q q.e[i] = q.e[i+1]; q.e[2] = null; /* ----------------------------------------------------- The target entry is now the successor's location ----------------------------------------------------- */ p = q; // node where entry was deleted System.out.println("Result: p = " + p); } /* *********************************************** Check for a possible underflow situation *********************************************** */ if ( p.e[0] == null ) { handleUnderflow(p, null); // Node p is empty // Second parameter is a subtree // hung under p } return old.value; // Return old value }

Psuedo code of handleUnderflow(Node p):

/* ------------------------------------------------------- handleUnderflow(p): handle the overflow condition in node p (p = empty !) Node format: p: {p1, k1, p2, k2, p3, k3, p4} k1, k2, k3 are keys (with values) p1, p2, p3, p4 are subtree pointers Node p (input) is empty - i.e., it has NO keys BUT: p.p1 points to the subtree of the underflow node ------------------------------------------------------- */ void handleUnderflow(Node p) { /* ---------------------------- Check if p is the root ---------------------------- */ if ( p == root ) { root = p.p1; // New root... return; // DONE ! } /* ------------------------------------------------------------- Solve underflow with a TRANSFER against your right sibling ------------------------------------------------------------- */ if ( p.right_sibling != null && p.right_sibling has >= 2 entries ) { /* ------------------------------------- Transfer p1 and k1 from right sibling See: click here ------------------------------------- */ s = p.right_sibling; pa = p.parent; i = index of subtree p in parent pa; // i = 1, 2 or 3 /* -------------------------------------------------- Example: if i == 1, then: pa: | p1 | k1 | p2 | k2 | p3 | k3 | p4 | / \ p s (s is right sibling of p) --------------------------------------------------- */ /* ---------------------- Transfer data into p ---------------------- */ p.k1 = pa.ki; // Transfer entry from parent p.p2 = s.p1; // Transfer left most subtree from sibling /* ----------------------------- Transfer data into parent pa ----------------------------- */ pa.ki = s.k1; // Transfer left most key from sibling delete p1 and k1 from s; return; // DONE... } /* ------------------------------------------------------------- Solve underflow with a TRANSFER against your left sibling ------------------------------------------------------------- */ else if ( p.left_sibling != null && p.left_sibling has >= 2 entries ) { /* ------------------------------------------------ Transfer p(Last) and k(Last) from left sibling See: click here ------------------------------------------------ */ s = p.left_sibling; pa = p.parent; i = index of subtree p in parent pa; // i = 2, 3 or 4 /* ---------------------------------------------- Example: if i == 3, then: pa: | p1 | k1 | p2 | k2 | p3 | k3 | p4 | / \ s p (s is left sibling of p) ----------------------------------------------- */ /* ---------------------- Transfer data into p ---------------------- */ p.k1 = pa.k(i-1); // Transfer entry from parent p.p2 = p.p1; // Green link p.p1 = s.p(Last); // Cyan link /* ----------------------------- Transfer data into parent pa ----------------------------- */ pa.k(i-1) = s.k(Last); delete p(Last) and k(Last) from s; return; // DONE... } /* ------------------------------------------------------------- Solve underflow with a MERGE with your right sibling ------------------------------------------------------------- */ else if ( p.right_sibling != null ) { /* --------------------------- Merge with right sibling See: click here ---------------------------*/ s = p.right_sibling; pa = p.parent; i = index of subtree p in parent pa; // i = 1, 2 or 3 /* -------------------------------------------------- Example: if i == 1, then: pa: | p1 | k1 | p2 | k2 | p3 | k3 | p4 | / \ p s (s is right sibling of p) --------------------------------------------------- */ p.k1 = pa.ki p.p2 = s.p1; p.k2 = s.k1; p.p3 = s.p2; pa.pi = p; delete pa.ki and pa.p(i+1) from pa; } else { /* --------------------------- Merge with left sibling See: click here ---------------------------*/ s = p.left_sibling; pa = p.parent; i = index of subtree p in parent pa; // i = 2, 3 or 4 /* ---------------------------------------------- Example: if i == 3, then: p(i-1) pi pa: | p1 | k1 | p2 | k2 | p3 | k3 | p4 | / \ s p (s is left sibling of p) ----------------------------------------------- */ s.k2 = pa.k(i-1); s.p3 = p.p1; pa.p(i-1) = s; delete pa.k(i-1) and pa.pi from pa; } /* --------------------------------------------- Check if the merged node has underflowed... --------------------------------------------- */ if ( pa has 0 entry ) { handleUnderflow(pa); // Recurse... } }

Java code:

public void handleUnderflow(Node p, Node Z) { /* ================================================ Check if the root node is empty Note: This is a base case of the recursion.... ================================================ */ if ( p == root ) { root = Z; // Delete the empty root node p return; } /* ------------------------------------------------------------- Find the position of p inside p's parent node p's parent --> | T0 | e0 | T1 | e1 | T2 | e2 | T3 | ^ ^ ^ ^ | | | | pos=0 pos=1 pos=2 pos=3 Which of the T? is p ???? (pos = 0, 1, 2, or 3) ---------------------------------------------------- */ Node parent; int pos; parent = p.parent; for ( pos = 0; pos < 4; pos++ ) { if ( parent.child[pos] == p ) break; } /* ------------------------------------------------------------- TRY a TRANSFER with your RIGHT sibling ------------------------------------------------------------- */ if ( (pos <= 2 && parent.child[pos+1] != null) /* p has a right sibling */ && parent.child[pos+1].e[1] != null /* R sibling has >= 2 entries */) { /* ----------------------------------------------------------- Legend to understand the transfer operation: (assume pos=1) pos pos+1 | | V V parent --> | T0 | e0 | T1 | *e1* | T2 | e2 | T3 | | | p R_sibling Entry sandwiched between pos and pos+1 is moved into p !!! ----------------------------------------------------------- */ Node R_sibling = parent.child[pos+1]; System.out.println("Underflow !!!! ===> Transfer with R sibling " + R_sibling); p.child[0] = Z; // Hang Z if ( Z != null ) Z.parent = p; p.e[0] = parent.e[pos]; // Transfer parent's entry p.child[1] = R_sibling.child[0]; // Transfer sibling's subtree if ( p.child[1] != null ) p.child[1].parent = p; parent.e[pos] = R_sibling.e[0]; // Move sibling entry to parent /* =================================== Delete e[0] in R_sibling =================================== */ for ( int i = 0; i < 2; i++ ) // ... accomplish by shifting { R_sibling.e[i] = R_sibling.e[i+1]; R_sibling.child[i] = R_sibling.child[i+1]; } R_sibling.e[2] = null; // e[2] is now empty R_sibling.child[3] = null; // child[3] is now empty return; // Done } /* ------------------------------------------------------------- TRY a TRANSFER with your LEFT sibling ------------------------------------------------------------- */ else if ( pos > 0 /* p has a left sibling */ && parent.child[pos-1].e[1] != null /* L sibling has >= 2 entries */) { /* ----------------------------------------------------------- Legend to understand the transfer operation: (assume pos=1) pos-1 pos | | V V parent --> | T0 | *e0* | T1 | e1 | T2 | e2 | T3 | | | L_sibling p Entry sandwiched between pos-1 and pos is moved into p !!! ----------------------------------------------------------- */ Node L_sibling = parent.child[pos-1]; int last; System.out.println("Underflow !!!! ===> Transfer with L sibling " + L_sibling); /* ------------------------------------- Find the last entry in L_sibling ------------------------------------- */ for ( last = 0; last < 3; last++ ) if ( L_sibling.e[last] == null ) break; if ( last >= 3 || L_sibling.e[last] == null ) last--; p.child[0] = L_sibling.child[last+1]; // Transfer sibling's subtree if ( p.child[0] != null ) p.child[0].parent = p; p.e[0] = parent.e[pos-1]; // Transfer parent's entry p.child[1] = Z; // Hang Z if ( Z != null ) Z.parent = p; parent.e[pos-1] = L_sibling.e[last]; // Move sibling entry to parent /* =================================== Delete e[lst] in L_sibling =================================== */ L_sibling.e[last] = null; L_sibling.child[last+1] = null; return; // Done } /* ======================================================== We MUST use a merge operation Legend of the position of p inside p's parent node p's parent --> | T0 | e0 | T1 | e1 | T2 | e2 | T3 | ^ ^ ^ ^ | | | | pos=0 pos=1 pos=2 pos=3 ======================================================== */ /* ------------------------------------------------------------- TRY a MERGE with your RIGHT sibling ------------------------------------------------------------- */ else if ( pos != 3 /* No Right sibling possible */ && parent.child[pos+1] != null /* There is a right sibling */) { /* ----------------------------------------------------------- Legend to understand the merge operation: (assume pos=1) pos pos+1 | | V V parent --> | T0 | e0 | T1 | *e1* | T2 | e2 | T3 | | | p R_sibling Entry sandwiched between pos and pos+1 is moved into p !!! ----------------------------------------------------------- */ Node R_sibling = parent.child[pos+1]; // R_sibling has ONLY 1 entry ! System.out.println("Underflow !!!! ===> MERGE with R sibling " + R_sibling); p.child[0] = Z; // Hang Z if ( Z != null ) Z.parent = p; p.e[0] = parent.e[pos]; // Transfer parent's entry p.child[1] = R_sibling.child[0]; // Transfer sibling's subtree if ( p.child[1] != null ) p.child[1] .parent = p; p.e[1] = R_sibling.e[0]; // Transfer sibling (ONLY) entry p.child[2] = R_sibling.child[1]; // Transfer sibling's subtree if ( p.child[2] != null ) p.child[2] .parent = p; /* ====================================== Delete parent.e[pos] in parent node ====================================== */ for ( int i = pos; i < 2; i++ ) { parent.e[i] = parent.e[i+1]; parent.child[i+1] = parent.child[i+2]; } parent.e[2] = null; parent.child[3] = null; if ( parent.e[0] == null ) handleUnderflow(parent, p); } else // pos == 3, we must merge LEFT ... { /* ----------------------------------------------------------- Legend to understand the transfer operation: (assume pos=1) pos-1 pos | | V V parent --> | T0 | *e0* | T1 | e1 | T2 | e2 | T3 | | | L_sibling p Entry sandwiched between pos-1 and pos is moved into p !!! ----------------------------------------------------------- */ Node L_sibling = parent.child[pos-1]; // L_sibling has 1 entry ! System.out.println("Underflow !!!! ===> MERGE with L sibling " + L_sibling); L_sibling.e[1] = parent.e[pos-1]; // Transfer parent's entry L_sibling.child[2] = Z; // Hang Z if ( Z != null ) Z.parent = p; /* ====================================== Delete parent.e[pos] in parent node ====================================== */ for ( int i = pos-1; i < 2; i++ ) { parent.e[i] = parent.e[i+1]; parent.child[i+1] = parent.child[i+2]; } parent.e[2] = null; parent.child[3] = null; if ( parent.e[0] == null ) handleUnderflow(parent, L_sibling); } }

Example Program: (Demo above code)

The Tree24.java Prog file: click here
The Node.java Prog file: click here
The Entry.java Prog file: click here
A test program TestProg.java Prog file: click here

How to run the program:

Right click on link(s) and save in a scratch directory
To compile: javac TestProg.java
To run: java TestProg

Sample output:

Legend: red denotes the next deleted entry darkred denotes the entries involved in op darkgreen shows when the involved entries end up 2:((m,6),(-),(-)) 3:((ka,6),(l,6),(-)) 1:((kb,6),(-),(-)) 0:((j,6),(k,6),(-)) 1:((h,8),(-),(-)) 2:((g,7),(-),(-)) 0:((e,5),(f,6),(-)) 0:((ba,6),(d,4),(i,9)) 1:((ca,6),(-),(-)) 1:((c,3),(-),(-)) 0:((bb,6),(-),(-)) 3:((b,2),(-),(-)) 2:((ae,6),(af,6),(-)) <--- will be replaced by (ae,6) 0:((ab,6),(ad,6),(ax,6)) 1:((ac,6),(-),(-)) 0:((a,1),(aa,6),(-)) ================================================================== == After remove(ad): 2:((m,6),(-),(-)) 3:((ka,6),(l,6),(-)) 1:((kb,6),(-),(-)) 0:((j,6),(k,6),(-)) 1:((h,8),(-),(-)) 2:((g,7),(-),(-)) 0:((e,5),(f,6),(-)) 0:((ba,6),(d,4),(i,9)) 1:((ca,6),(-),(-)) 1:((c,3),(-),(-)) 0:((bb,6),(-),(-)) 3:((b,2),(-),(-)) 2:((af,6),(-),(-)) 0:((ab,6),(ae,6),(ax,6)) 1:((ac,6),(-),(-)) 0:((a,1),(aa,6),(-)) <---- will TRANSFER with Left sibling ==================================================== Underflow !!!! ===> Transfer with L sibling ((a,1),(aa,6),(-)) == After remove(ac): 2:((m,6),(-),(-)) 3:((ka,6),(l,6),(-)) 1:((kb,6),(-),(-)) 0:((j,6),(k,6),(-)) 1:((h,8),(-),(-)) 2:((g,7),(-),(-)) 0:((e,5),(f,6),(-)) 0:((ba,6),(d,4),(i,9)) 1:((ca,6),(-),(-)) 1:((c,3),(-),(-)) 0:((bb,6),(-),(-)) 3:((b,2),(-),(-)) 2:((af,6),(-),(-)) <---- will MERGE with Left sibling 0:((aa,6),(ae,6),(ax,6)) 1:((ab,6),(-),(-)) 0:((a,1),(-),(-)) ======================================== Underflow !!!! ===> MERGE with L sibling ((af,6),(-),(-)) == After remove(b): 2:((m,6),(-),(-)) 3:((ka,6),(l,6),(-)) 1:((kb,6),(-),(-)) 0:((j,6),(k,6),(-)) 1:((h,8),(-),(-)) 2:((g,7),(-),(-)) 0:((e,5),(f,6),(-)) 0:((ba,6),(d,4),(i,9)) 1:((ca,6),(-),(-)) 1:((c,3),(-),(-)) 0:((bb,6),(-),(-)) 2:((af,6),(ax,6),(-)) 0:((aa,6),(ae,6),(-)) 1:((ab,6),(-),(-)) 0:((a,1),(-),(-))