---

Review: priority queue (CS171 stuff)

---

• Priority queue

  • The priority queue was discussed in CS171:

    click here

    This webpage is a brief review of that material....

    ---

  • Priority queue:

    A data structure where the data item are stored in the order based on some priority field

    ---

    ---

  • The operations that is allowed on a priority queue are:

    size() = return the number of entries in the priority queue isEmpty() = test if the priority queue is empty insert(k,v) = insert the entry (k,v) in the priority queue (the ordering will be based on the value of the key k peek() = return the entry with the minimum key value in the priority queue without removing it (from the priority queue) poll() = return the entry with the minimum key value in the priority queue and remove it from the priority queue

    ---

  • Comments:

    The priority queue store similar entries as the map that we have studied But: the operations defined on a priotity queue is less powerful than those for a map: peek() and poll() will only return the entry with the smallest value of the key !!! Result: We can use a more simpler data structure called the heap to achieve O(log(n)) performance

    ---

  • Note:

    A heap is not a Binary search tree (i.e., the left subtree can contain keys that are larger than the parent, and the right subtree can contain keys that are smaller than the key stored in the parent node).

  ---

  ---

  ---

  ---

• Review: heap
  • Heap: a binary tree with the following properties

    The binary tree is complete: All levels of the binary tree, except for the last level, are completely filled. In addition, nodes on the last level of the binary tree are packed to the left The key value k stored in the nodes of any subtree of the node (k0.v0) statifies: k0 ≤ k

    ---

  • Examples:

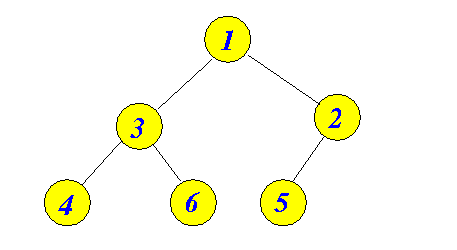
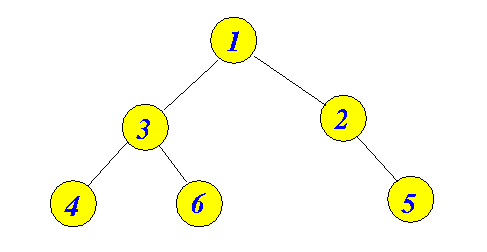
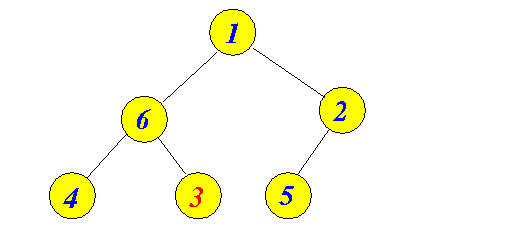
    The is a heap: Notice: Binary tree is complete Key values stored in a subtree are   ≤   key value stored in root node of subtree The is a not a heap: because the binary tree is not a complete tree (not packed to the left) The is a not a heap: because the key 3 stored in a subtree of the node 6 has a smaller key value

  ---

  ---

  ---

  ---

• Inserting into a heap
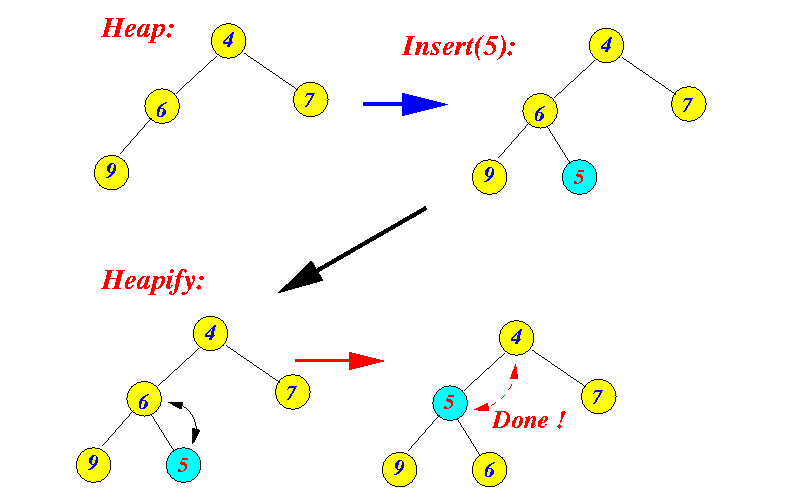
  • Heap insertion algorithm:

    Insert the new entry into the left-most free position on the lowest level (to perserve completeness) "Heapify" using the filter up (a.k.a. bubble up) operation: current = newly inserted entry while ( current != root ) { parent = current.parent; if ( current.key < parent.key ) { swap( current, parent ); current = parent; } else { break; } }

    ---

  • Example 1:

    ---

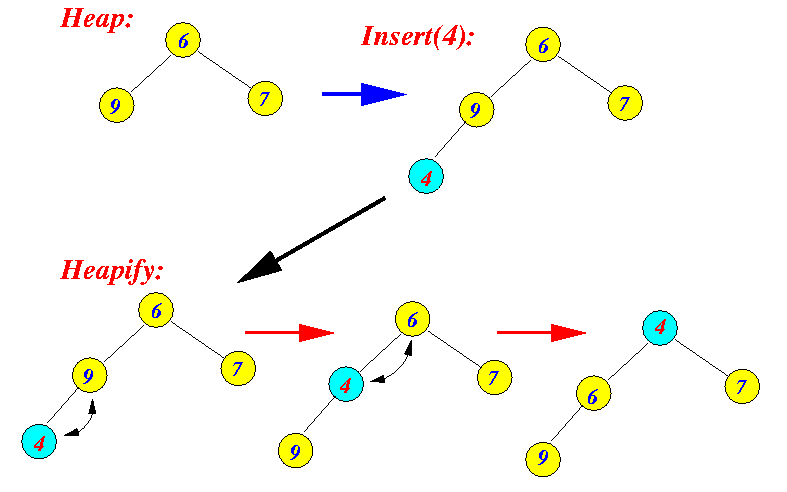
  • Example 2:

  ---

  ---

  ---

  ---

• Deleting from a heap
  • Fact:

    The poll() method will always remove the root node from a heap because: The root node has the smallest key value among all the entries stored in the heap !!!

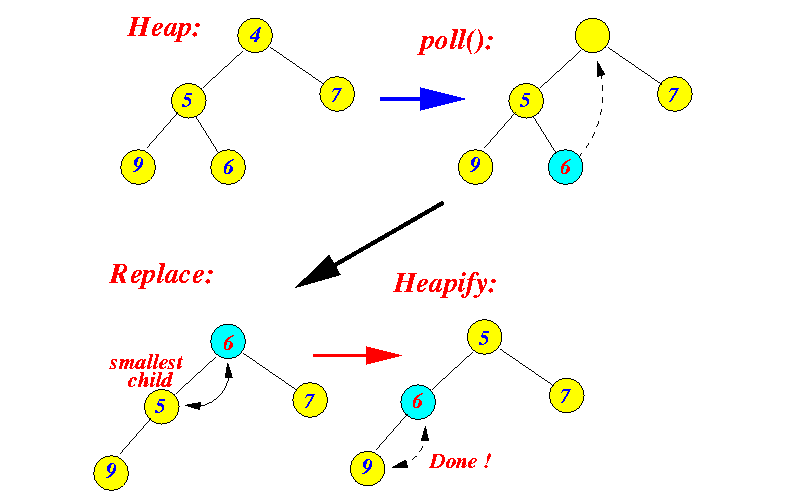
  • Heap deletion algorithm:

    Remove the root node Replace the root node with the left-most entry on the lowest level (again, to perserve completeness) "Heapify" using the filter down (a.k.a. bubble down) operation: current = root node while ( current != a leaf node ) { min_key = min( left.key, right.key) ; if ( min_key < current.key ) { swap( current, node with min_key ); current = node with min_key; } else { break; } }

    ---

  • Example:

  ---

  ---

• Implementation
  • As discussed in CS171, a heap is usually implemented as a array:

    ---

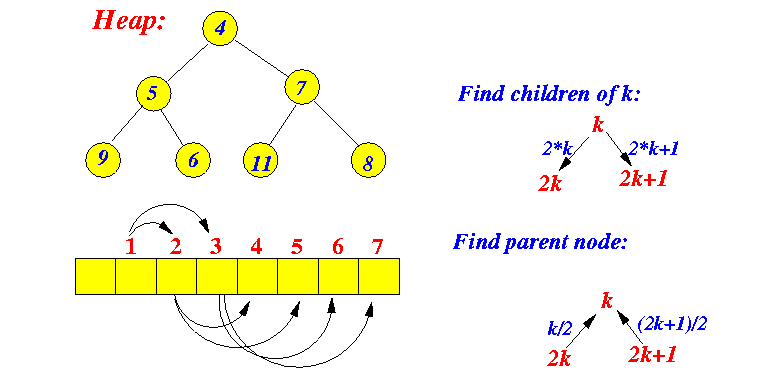
  • To find the indices of the children nodes of node k, use indices:

    2*k and 2*k + 1

  • To find the index of the parent node of node x, use index:

    x/2

    ---

  • Example Program: (adapted from the CS171 material)                                                
    • The Heap implementation Prog file: click here

    • A test prog file: click here

    How to run the program:

    Right click on link(s) and save in a scratch directory To compile:   javac TestPQ.java To run:          java TestPQ