- The unbounded knapsack problem:
- Given N types of items:
- The item type i has
a weight wi
- The item type i has a value vi
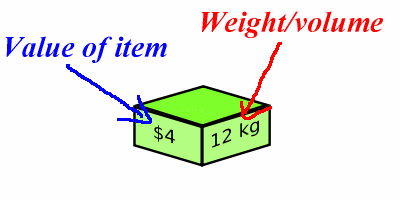
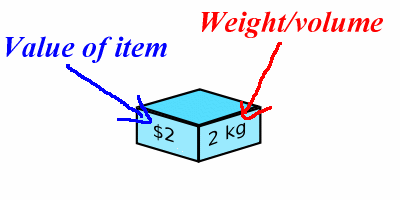
... Unbounded referes to:
- There are an unbounded
(= infinite) number
of
each type of item available
(I.e.: unbounded supply)
- The item type i has
a weight wi
- Given a knapsack with
capacity W:

- Problem:
- Pack as many items into
the knapsack
such that the
total value of the
items packed is
maximized
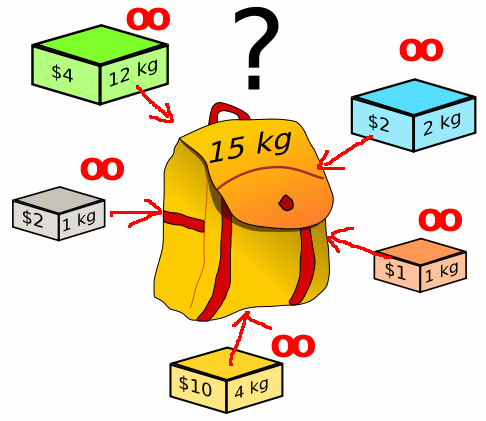
Note: you cannot exceed the capacity of the knapsack !
- Pack as many items into
the knapsack
such that the
total value of the
items packed is
maximized
- Given N types of items:
- Formal description:
- Define:
- x1 = # items of type 1 packed into the knapsack
- x2 = # items of type 2 packed into the knapsack
- ...
- xN = # items of type N packed into the knapsack
- Then:
- Total weight of item packed =
w1 × x1 +
w2 × x2 + ...
+ wN × xN
- Total value of item packed = v1 × x1 + v2 × x2 + ... + vN × xN
- Total weight of item packed =
w1 × x1 +
w2 × x2 + ...
+ wN × xN
- The unconstrained knapsack problem:
max: v1×x1 + v2×x2 + ... + vN×xN s.t.: w1×x1 + w2×x2 + ... + wN×xN ≤ W x1, x2, ..., xN integers
- Define:
- Observation:
- I can never exhaust
any item
because there are
an unbounded supply of items.
- Therefore:
- The technique used in the 0,1 knapsack problem cannot be used.
- I can never exhaust
any item
because there are
an unbounded supply of items.
- How to
solve an
unbounded knapsack problem
using the
solution
of smaller
unbounded knapsack problems:
- The first item
packed into the knapsack must be
one of these items:
- Item 1
- In that case, the knapsack has
a remaining capacity of
W − w1
- I can delegate this smaller
problem for someone else to solve:
- Maximize the value
(packing the same N items)
in a knapsack of
capacity
W − w1
(Remember: we have an unbounded number of items of each type !!!)
Let:
sol1 = solution of the smaller knapsack problem
(i.e., packing the knapsack of capacity W − w1)
- Maximize the value
(packing the same N items)
in a knapsack of
capacity
W − w1
- In that case, the knapsack has
a remaining capacity of
W − w1
- Item 2:
- In that case, the knapsack has
a remaining capacity of
W − w2
- I can delegate this smaller
problem for someone else to solve:
- Maximize the value (packing the same N items) in a knapsack of capacity W − w2
Let:
sol2 = solution of the smaller knapsack problem
(i.e., packing the knapsack of capacity W − w2)
- In that case, the knapsack has
a remaining capacity of
W − w2
- And so on
- Item 1
- How to
use the
solution of each
smaller problems
to solve my original problem:
- The first item packed was
item 1:
- The value in
my knapsack is equal to:
mySol1 = sol1 + v1
because I can add item 1 to the knapsack
- The value in
my knapsack is equal to:
- The first item packed was
item 2:
- The value in
my knapsack is equal to:
mySol1 = sol1 + v2
because I can add item 2 to the knapsack
- The value in
my knapsack is equal to:
- And so on...
- The first item packed was
item 1:
- The maximum value is therefore
the following:
maximum value packed in knapsack of capacity W = max ( mySol1, mySol2, ....., mySolN )
- The first item
packed into the knapsack must be
one of these items:
- Schematically:
- The divide step:
make
someones else solve
smaller problems
that can help you solve your
original problem:
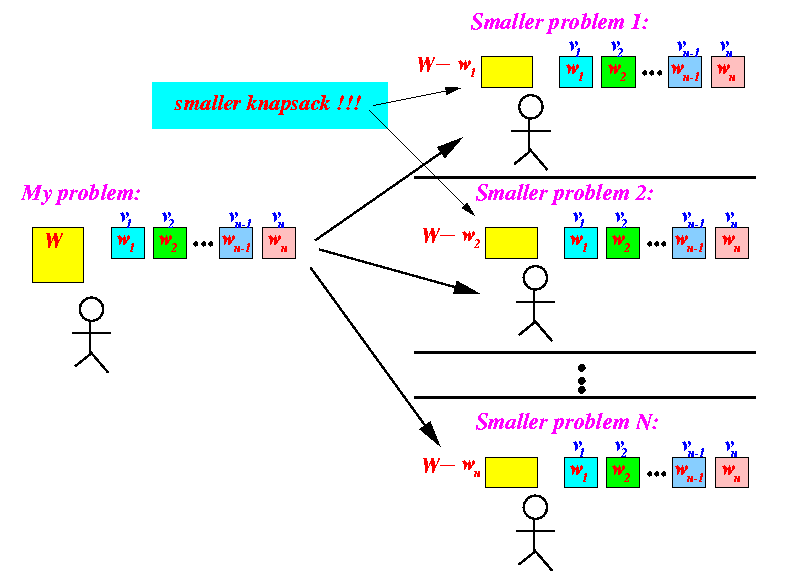
- Each one of the helpers come back with his/her
solution:
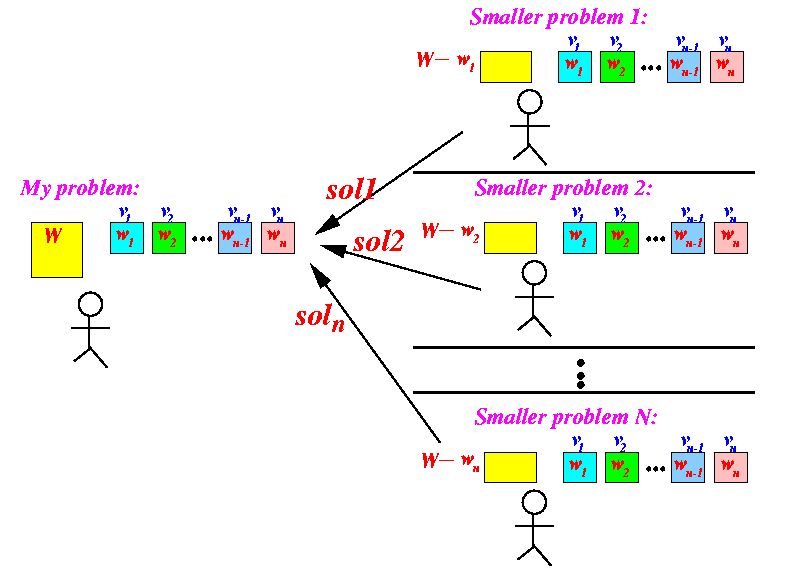
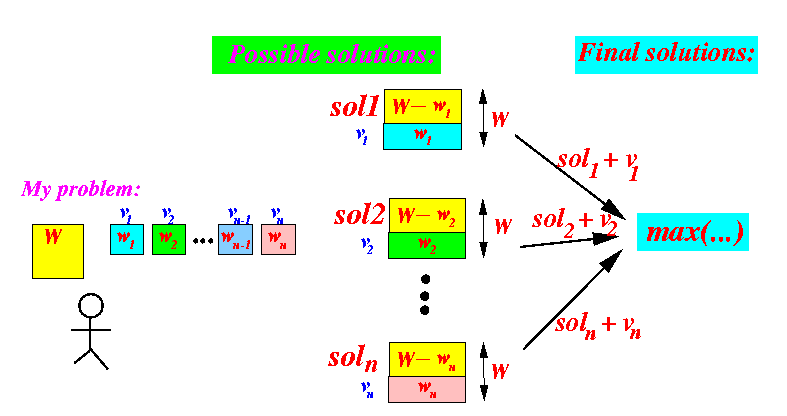
- I can find
my solution
using the
solutions from
the helpers:
- The divide step:
make
someones else solve
smaller problems
that can help you solve your
original problem:
- Caveat:
- You can only pack
the item k into
the knapsack if:
W ≥ wi !!!
- You can only pack
the item k into
the knapsack if:
- Define:
- M(v[], w[], C) =
the maximum value
of
v1×x1 + v2×x2
+ ... + vN×xN
subject to: w1×x1 + w2×x2 + ... + wN×xN ≤ C
- M(v[], w[], C) =
the maximum value
of
v1×x1 + v2×x2
+ ... + vN×xN
- The divide and conquer
procedure for the
unbounded knapsack problem:
M( v[], w[], C ) { int[] sol, mySol, myFinalSol; // Let us not worry about the base cases for now /* ============================================== Divide and conquer procedure ============================================== */ /* --------------------------------------- Solve the appropriate smaller problems --------------------------------------- */ for ( i = 1; i ≤ N; i++ ) { if ( C ≥ w[i] ) sol[i] = M( v, w, C-w[i] ); // Knapsack capacity reduced by w[i] // because it has item i packed in // it already else sol[i] = 0; // Not enough space to pack item i } /* --------------------------------------------- Use the solutions to the smaller problems to solve original problem --------------------------------------------- */ for ( i = 1; i ≤ N; i++ ) { if ( C ≥ w[i] ) mySol[i] = sol[i] + v[i]; // Value is increased by v[i] // because it has item i packed in // it already else mySol[i] = 0; // Not enough space to pack item i } /* ************************* Find the best (maximum) ************************* */ myFinalSol = mySol[1]; for ( i = 2; i ≤ N; i++ ) if ( mySol[i] > myFinalSol ) myFinalSol = mySol[i]; return myFinalSol; }
- Base case:
- When the knapsack is full,
you cannot pack
any item into the knapsack
Therefore, the total value of a 0 capacity knapsack = 0
In other words:
M(v, w, 0) = 0; (can't packet anything into a 0-capacity knapsack) - When the knapsack is full,
you cannot pack
any item into the knapsack
- Psuedo code
(N = # different items) M( v[], w[], C ) { int[] sol, mySol, myFinalSol; /* *************************************** Base case *************************************** */ if ( C == 0 ) return 0; /* ============================================== Divide and conquer procedure ============================================== */ /* --------------------------------------- Solve the appropriate smaller problems --------------------------------------- */ for ( i = 1; i ≤ N; i++ ) { if ( C ≥ w[i] ) sol[i] = M( v, w, C-w[i] ); // Knapsack capacity reduced by w[i] // because it has item i packed in // it already else sol[i] = 0; // Not enough space to pack item i } /* --------------------------------------------- Use the solutions to the smaller problems to solve original problem --------------------------------------------- */ for ( i = 1; i ≤ N; i++ ) { if ( C ≥ w[i] ) mySol[i] = sol[i] + v[i]; // Value is increased by v[i] // because it has item i packed in // it already else mySol[i] = 0; // Not enough space to pack item i } /* ************************* Find the best (maximum) ************************* */ myFinalSol = mySol[1]; for ( i = 2; i ≤ N; i++ ) if ( mySol[i] > myFinalSol ) myFinalSol = mySol[i]; return myFinalSol; }
- Java Code:
(main difference with pseudo code is:
I have to use array indices
that start at
0)
/* ======================================================== M(C) = max value achieved by knapsack with capacity C ======================================================== */ static int M(int[] v, int[] w, int C) { int[] sol, mySol; int i, myFinalSol; sol = new int[v.length]; mySol = new int[v.length]; /* --------------------------- Base cases --------------------------- */ if ( C == 0 ) { return(0); } /* ============================================== Divide and conquer procedure ============================================== */ /* --------------------------------------- Solve the appropriate smaller problems --------------------------------------- */ for ( i = 0; i < v.length; i++ ) { if ( C >= w[i] ) sol[i] = M( v, w, C-w[i] ); // Knapsack capacity reduced by w[i] // because it has item i packed in // it already else sol[i] = 0; // Not enough space to pack item i } /* --------------------------------------------- Use the solutions to the smaller problems to solve original problem --------------------------------------------- */ for ( i = 0; i < v.length; i++ ) { if ( C >= w[i] ) mySol[i] = sol[i] + v[i]; // Value is increased by v[i] // because it has item i packed in // it already else mySol[i] = 0; // Not enough space to pack item i } /* ************************* Find the best (maximum) ************************* */ myFinalSol = mySol[0]; for ( i = 1; i < v.length; i++ ) if ( mySol[i] > myFinalSol ) myFinalSol = mySol[i]; return myFinalSol; // Return the overal best solution }
- Example Program:
(Demo above code)

- Prog file: click here
How to run the program:
- Right click on link(s) and
save in a scratch directory
- To compile: javac Knapsack_unbounded1.java
- To run: java Knapsack_unbounded1
- Data structure:
- The recursive method
has one parameter:
static int M(int[] v, int[] w, int C)
where C will vary from W (= capacity of the knapsack) to 0
(The parameters v[] and w[] do not change and are not real parameters !!!)
Therefore, to store the results computed by the recursive method, we will a one dimensional array:
int[] M = new int[ W+1 ] ;
- The recursive method
has one parameter:
- The base case:
if ( C == 0 ) return 0;will compute the following result in the result array M[]:
M[ 0 ] = 0 ;
- The recursive case:
- In the recursive part,
the algorithm computes
myFinalSol which is
the value
M[C]
--- since the memoization code will stored
myFinalSol in
M[C]
(BTW: C is the
parameter of the call !)
/* --------------------------------------- Solve the appropriate smaller problems --------------------------------------- */ for ( i = 0; i < v.length; i++ ) { if ( C >= w[i] ) sol[i] = M( v, w, C-w[i] ); // Knapsack capacity reduced by w[i] // because it has item i packed in // it already else sol[i] = 0; // Not enough space to pack item i } /* --------------------------------------------- Use the solutions to the smaller problems to solve original problem --------------------------------------------- */ for ( i = 0; i < v.length; i++ ) { if ( C >= w[i] ) mySol[i] = sol[i] + v[i]; // Value is increased by v[i] // because it has item i packed in // it already else mySol[i] = 0; // Not enough space to pack item i } /* ************************* Find the best (maximum) ************************* */ myFinalSol = mySol[0]; for ( i = 1; i < v.length; i++ ) if ( mySol[i] > myFinalSol ) myFinalSol = mySol[i]; return myFinalSol; // Return value of M(v,w,C)
- Therefore,
M[C] is computed as follows:
/* --------------------------------------- Solve the appropriate smaller problems --------------------------------------- */ for ( i = 0; i < v.length; i++ ) { if ( C >= w[i] ) sol[i] = M[ C-w[i] ]; // Knapsack capacity reduced by w[i] // because it has item i packed in // it already else sol[i] = 0; // Not enough space to pack item i } /* --------------------------------------------- Use the solutions to the smaller problems to solve original problem --------------------------------------------- */ for ( i = 0; i < v.length; i++ ) { if ( C >= w[i] ) mySol[i] = sol[i] + v[i]; // Value is increased by v[i] // because it has item i packed in // it already else mySol[i] = 0; // Not enough space to pack item i } /* ************************* Find the best (maximum) ************************* */ M[C] = mySol[0]; for ( i = 1; i < v.length; i++ ) if ( mySol[i] > myFinalSol ) M[C] = mySol[i];
- We must compute M[C]
in the following order:
for ( C = 1; C ≤ W; C++ ) compute W[C] .... (see above)
- In the recursive part,
the algorithm computes
myFinalSol which is
the value
M[C]
--- since the memoization code will stored
myFinalSol in
M[C]
(BTW: C is the
parameter of the call !)
- Java code:
/* ======================================================== M_dp(W) = max value achieved by knapsack with capacity W ======================================================== */ static int M_dp(int[] v, int[] w, int W) { int[] sol, mySol; int i, myFinalSol; int[] M; // Data structure to store results int C; // Index to run through M[] sol = new int[v.length]; mySol = new int[v.length]; M = new int[W + 1]; // Create array /* --------------------------- Base cases --------------------------- */ M[0] = 0; /* ============================================== The other values M[C] ============================================== */ for ( C = 1; C <= W; C++ ) { /* --------------------------------------- Solve the appropriate smaller problems --------------------------------------- */ for ( i = 0; i < v.length; i++ ) { if ( C >= w[i] ) sol[i] = M[ C-w[i] ]; // Knapsack capacity reduced by w[i] // because it has item i packed in // it already else sol[i] = 0; // Not enough space to pack item i } /* --------------------------------------------- Use the solutions to the smaller problems to solve original problem --------------------------------------------- */ for ( i = 0; i < v.length; i++ ) { if ( C >= w[i] ) mySol[i] = sol[i] + v[i]; // Value is increased by v[i] // because it has item i packed in // it already else mySol[i] = 0; // Not enough space to pack item i } /* ************************* Find the best (maximum) ************************* */ M[C] = mySol[0]; for ( i = 1; i < v.length; i++ ) if ( mySol[i] > M[C] ) M[C] = mySol[i]; } return M[ W ]; // Return best value for knapsack of cap = W }
- Example Program:
(Demo above code)

- Prog file: click here
How to run the program:
- Right click on link(s) and
save in a scratch directory
- To compile: javac Knapsack_unbounded1_dp.java
- To run: java Knapsack_unbounded1_dp
- The main loop of the Dyn. Progrm.
is:
for ( C = 1; C <= W; C++ ) { for ( i = 0; i < v.length; i++ ) { .... } } // W = capacity of knapsack // v.length = # different items = NTherefore:
- Running time = O(WN)