Strength and
weakness of
a hash table
- A hash table is
fast when
entries are
not
clustered:
+---+---+---+---+---+---+---+---+---+---+---+---+
entry[] = | A | | B | | C | | D | | E | | F | |
+---+---+---+---+---+---+---+---+---+---+---+---+
|
- In this situation,
get( ),
put( ) and
remove( ) will
finish in
O(1) time:
- The search will
find the
key
immediately
in the hash bucket
- Or else, the
search will
terminate in the
next step because
it finds a empty (null) bucket
|
- A hash table is
slower when
entries are
clustered:
Suppose: H(A) = H(B) = H(C) = H(D) = H(E) = 1
+---+---+---+---+---+---+---+---+---+---+---+---+
entry[] = | A | B | C | D | E | | | | | | | |
+---+---+---+---+---+---+---+---+---+---+---+---+
|
To find the
key E, we need
more
comparison operations
|
Runtime analysis of the
Linear Probing open addressing method
- Worst case
running time of
hashing with
linear probing:
- When the hash table is
full:
+---+---+---+---+---+---+---+---+---+---+---+---+
entry[] = | A | B | C | D | E | F | G | H | I | J | K | L |
+---+---+---+---+---+---+---+---+---+---+---+---+
|
then:
- get(),
put() and
remove()
may
need to
scan the
entire
hash table to
find the entry...
|
- Therefore:
|
|
Prelude to
average case running time analysis
of linear probing
- Mathematical
average:
Suppose you roll a six-sided die:
When you roll 1: you win $1
When you roll 2: you win $5
When you roll 3: you win $1
When you roll 4: you win $5
When you roll 5: you win $1
When you roll 6: you win $10
|
- What is your
average winning
per dice roll ???
|
Prelude to
average case running time analysis
of linear probing
- Mathematical
average:
Suppose you roll a six-sided die:
When you roll 1: you win $1
When you roll 2: you win $5
When you roll 3: you win $1
When you roll 4: you win $5
When you roll 5: you win $1
When you roll 6: you win $10
|
- What is your
average winning
per dice roll ???
In 1/6 of the rolls, you will roll a 1:
In 1/6 of the rolls, you will roll a 2:
In 1/6 of the rolls, you will roll a 3:
In 1/6 of the rolls, you will roll a 4:
In 1/6 of the rolls, you will roll a 5:
In 1/6 of the rolls, you will roll a 6:
|
|
Prelude to
average case running time analysis
of linear probing
- Mathematical
average:
Suppose you roll a six-sided die:
When you roll 1: you win $1
When you roll 2: you win $5
When you roll 3: you win $1
When you roll 4: you win $5
When you roll 5: you win $1
When you roll 6: you win $10
|
- What is your
average winning
per dice roll ???
In 1/6 of the rolls, you will roll a 1: you win $1 --> $1/6
In 1/6 of the rolls, you will roll a 2: you win $5 --> $5/6
In 1/6 of the rolls, you will roll a 3: you win $1 --> $1/6
In 1/6 of the rolls, you will roll a 4: you win $5 --> $5/6
In 1/6 of the rolls, you will roll a 5: you win $1 --> $1/6
In 1/6 of the rolls, you will roll a 6: you win $10 --> $10/6
|
|
Prelude to
average case running time analysis
of linear probing
- Mathematical
average:
Suppose you roll a six-sided die:
When you roll 1: you win $1
When you roll 2: you win $5
When you roll 3: you win $1
When you roll 4: you win $5
When you roll 5: you win $1
When you roll 6: you win $10
|
- What is your
average winning
per dice roll ???
In 1/6 of the rolls, you will roll a 1: you win $1 --> $1/6
In 1/6 of the rolls, you will roll a 2: you win $5 --> $5/6
In 1/6 of the rolls, you will roll a 3: you win $1 --> $1/6
In 1/6 of the rolls, you will roll a 4: you win $5 --> $5/6
In 1/6 of the rolls, you will roll a 5: you win $1 --> $1/6
In 1/6 of the rolls, you will roll a 6: you win $10 --> $10/6
Winning per roll = 1/6 + 5/6 + 1/6 + 5/6 + 1/6 + 10/6 =$3 5/6
|
|
Average case running time analysis
of linear probing
- Consider the
get( ) algorithm
using linear probing:
public V get(K k)
{
int hashIdx = H(k); // Find the hash index for key k
int i = hashIdx;
do
{
if ( entry[i] == null ) // Is entry empty ?
{
return null; // NOT found
}
else if ( bucket[i] == AVAILABLE )
{
// DO NOT TEST bucket[i] !!! But we need to continue...
}
else if ( entry[i].key == k ) // FOUND
{
return bucket[i].value;
}
i = (i + 1)%M; // Check in next hash table entry
} while ( i != hashIdx ) // All entries searched
return null; // NOT found
}
|
- Get( ) will
return when
it find (1) an empty bucket or
(2) the key k
|
Average case running time analysis
of linear probing
- Consider the
put( ) algorithm
using linear probing:
public void put(K k, V v)
{
int hashIdx = H(k); // Find the hash index for key k
int i = hashIdx;
int firstAvail = -1; // -1 means: no AVAILABLE entry found (yet)
do // Search for key k in the hash table
{
if ( entry[i] == null ) // Is entry empty ?
{
if ( firstAvail == -1 ) // No AVAILABLE bucket found
bucket[i] = new Entry<>(k,v);
else // An AVAILABLE bucket found
bucket[firstAvail] = new Entry<>(k,v);
return;
}
else if ( bucket[i] == AVAILABLE )
{
if ( firstAvail == -1 ) firstAvail = i;
}
else if ( entry[i].key == k ) // Does entry contains key k ?
{
bucket[i].value = v;
return;
}
i = (i + 1)%M; // Check in next hash table entry
} while ( i != hashIdx ) // All entries searched !
if ( firstAvail == -1 )
System.out.println("Full");
else
bucket[firstAvail] = new Entry<>(k,v);
}
|
- Put( ) will
also
return when
it find (1) an empty bucket or
(2) the key k
|
Average case running time analysis
of linear probing
- Consider the
remove( ) algorithm
using linear probing:
public V remove(K k) // Return the value associated with key k
{
int hashIdx = hashValue(k);
int i = hashIdx;
do
{
if ( entry[i] == null ) // Is bucket empty ?
{
return null;
}
else if ( bucket[i] == AVAILABLE )
{
// DO NOT TEST bucket[i] !!! But we need to continue...
}
else if ( entry[i].key == k ) // Does bucket contains key k ?
{
V retVal = bucket[i].value;
bucket[i] = AVAILABLE; // Delete the entry
return retVal;
}
i = (i + 1)%capacity; // Check in next hash table bucket
} while ( i != hashIdx ); // All entries searched !
return null; // Not found
}
|
- Remove( ) will
also
return when
it find (1) an empty bucket or
(2) the key k
|
Average case running time analysis
of linear probing
- Simplifying assumption:
- To keep the
running time analysis
simple, we will
assume that:
- There are
no
AVAILABLE
entries
in the hash table
|
|
- From the observation of the
get( ),
put( ) and
remove( )
algorithms:
- The
running time of
get( ),
put( ) and
remove( )
depends on
the
# entries
we need to
check
in order to
find:
- The key k
or
- An empty bucket
|
|
- The
worst case
running time is when:
- The search ends by
finding an
empty bucket
(takes longer time)
|
- Therefore:
average
running time of
get( ),
put( ) and
remove( )
=
average
# compare operations
to find an
empty bucket
|
Load factor and
the probabibility of
finding an empty bucket
- Definition:
load factor
(a.k.a.
occupancy level)
# entries in hash table n
Load factor (α) = -------------------------- = ---
size of the hash table M
|
- The probability (= likelihood)
that a hash bucket is
occupied:
# entries in the hash table
P[ bucket i is occupied ] = -----------------------------------
Total # buckets in the hash table
= α
|
- The probability (= likelihood)
that a hash bucket is
empty:
P[ bucket i is empty ] = 1 - α
|
|
Computing the average runtime of
get( ),
put( ) and
remove( )
- The
average
running time of
get( ),
put( ) and
remove( ) is
found by
computing:
-
How often (frequent)
do we need to
check
1 entry
to find an empty slot
(= f1)
How many operations
did we perform in
this case
(= c1)
-
How often (frequent)
do we need to
check
2 entries
to find an empty slot
(= f2)
How many operations
did we perform in
this case
(= c2)
-
How often (frequent)
do we need to
check
3 entries
to find an empty slot
(= f3)
How many operations
did we perform in
this case
(= c3)
-
And so on...
|
- The
average
running time of
get( ),
put( ) and
remove( ) is
equal to:
Avg running time = f1c1 + f2c2 + f3c3+ ...
|
|
How often (frequent)
do we need to
check 1 entry
to find an
empty slot
- The probability (= likelihood)
of finding a
bucket to be
empty =
1 −
α
- We
check
1 entry
(= the
hash bucket)
and finds an
empty bucket:
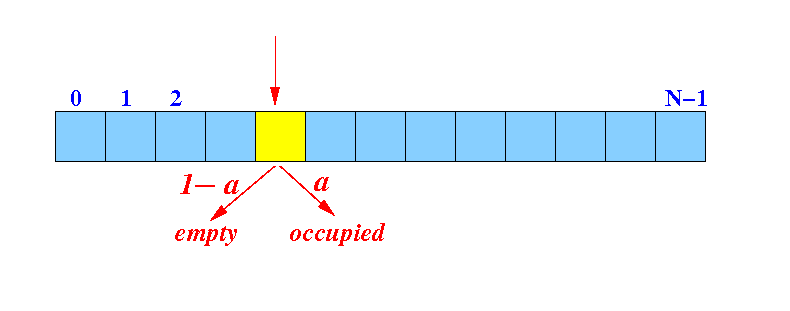
Probability:
P[ check 1 bucket to find an empty bucket ] = 1 - α (= f1)
# check operations performed in this case = 1 (= c1)
|
|
How often (frequent)
do we need to
check 2 entries
to find an
empty slot
- The probability (= likelihood)
of finding a
bucket to be
empty =
1 −
α
- We
check
2 entries
(= the
hash bucket +
next bucket)
and finds an
empty bucket:
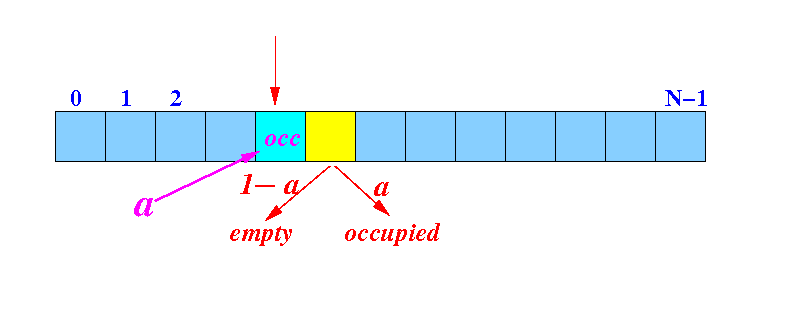
Probability:
P[ check 2 buckets to find an empty bucket ] = α(1 - α) (= f2)
# check operations performed in this case = 2 (= c2)
|
|
How often (frequent)
do we need to
check 3 entries
to find an
empty slot
- The probability (= likelihood)
of finding a
bucket to be
empty =
1 −
α
- We
check
3 entries
(= the
hash bucket +
2 more buckets)
and finds an
empty bucket:
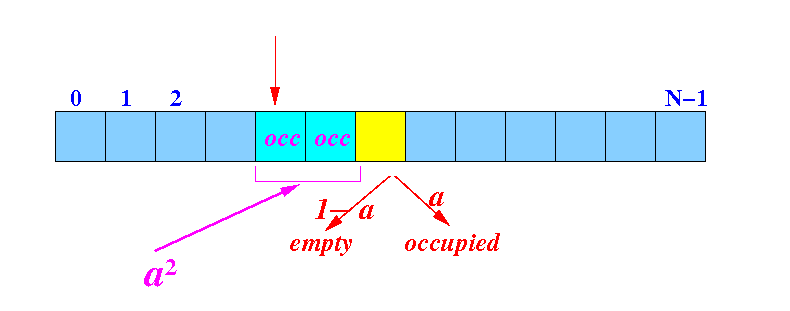
Probability:
P[ check 3 buckets to find an empty bucket ] = α2(1 - α) (= f3)
# check operations performed in this case = 3 (= c3)
|
|
Average case running time analysis
of linear probing
- The
average
running time of
get( ),
put( ) and
remove( ) is
equal to:
Avg running time = f1c1 + f2c2 + f3c3+ ...
= (1-α).1 + α(1-α).2 + α2(1-α).3 + ...
= (1-α) [ 1 + 2α1 + 3α2 + 4α3 + ... ]
|
- We will use
MatLab to
compute the
sum:
S = 1 + 2α1 + 3α2 + 4α3 + ... = 1/(1 - α)^2
MatLab commands:
matlab -nodesktop
syms a k
assume(a > 0 & a < 1)
symsum( (k+1)*(a^k), k, 0, inf)
Answer: 1/(a - 1)^2
|
-
The
average
running time of
get( ),
put( ) and
remove( ) is
equal to:
Avg running time = (1 - α)/(1 - α)^2 = 1/(1 - α)
|
|
Interpreting the
average case running time analysis
of linear probing
-
α =
the load factor or
occupancy level
- The probability (= likelihood)
of finding a
bucket to be
empty =
1 −
α
- The average
runtime of
get( ),
put( ) and
remove( ) is
the
average
# of compare operations
performed to find an
empty bucket:
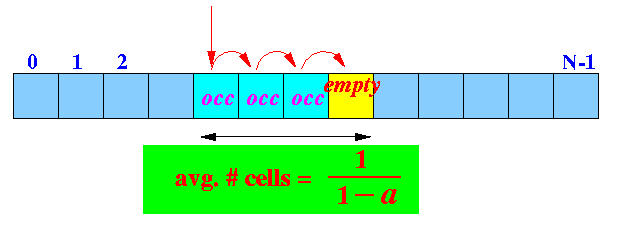
- From the analysis:
Average # compare operation used = 1/(1 - α)
|
- Example:
If α = 10%, then: (because 90% of the time you find an empty bucket)
Avg # buckets searched = 1/(1 - 0.1) = 1/0.9 = 1.1
|
|
❮
❯



