Closed Addressing vs. Open Addressing

  • Closed Addressing:

    • In closed addressing, each key is always stored in the hash bucket where the key is hashed to.

      • Closed addressing must use some data structure (e.g.: linked list) to store multiple entries in the same bucket

  • Example of closed addressing:   a hash table using separate chaining

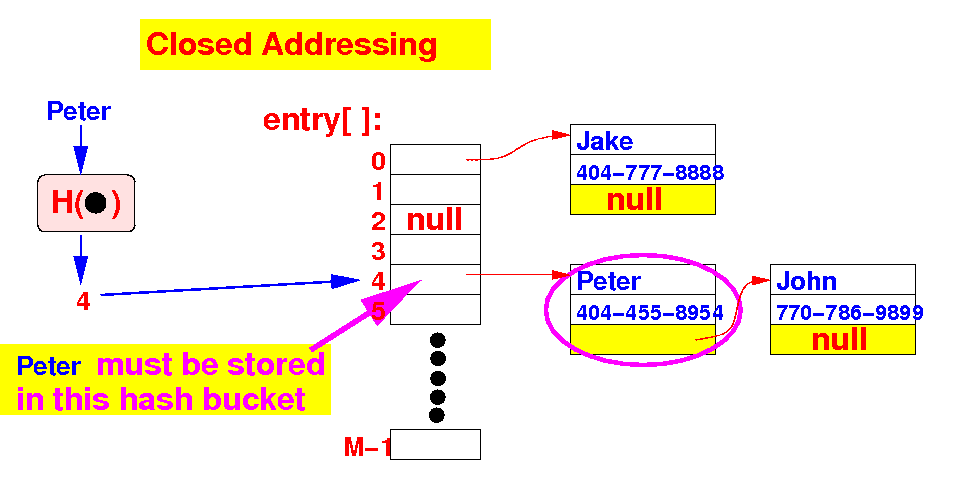
Closed Addressing vs. Open Addressing

  • Open Addressing:

    • In open addressing, each hash bucket will store at most one hash table entry

      • In open addressing, a key may be stored in different hash bucket than where the key was hashed to.

  • Example of open addressing:   Peter hashed into bucket 4 but is stored in bucket 5

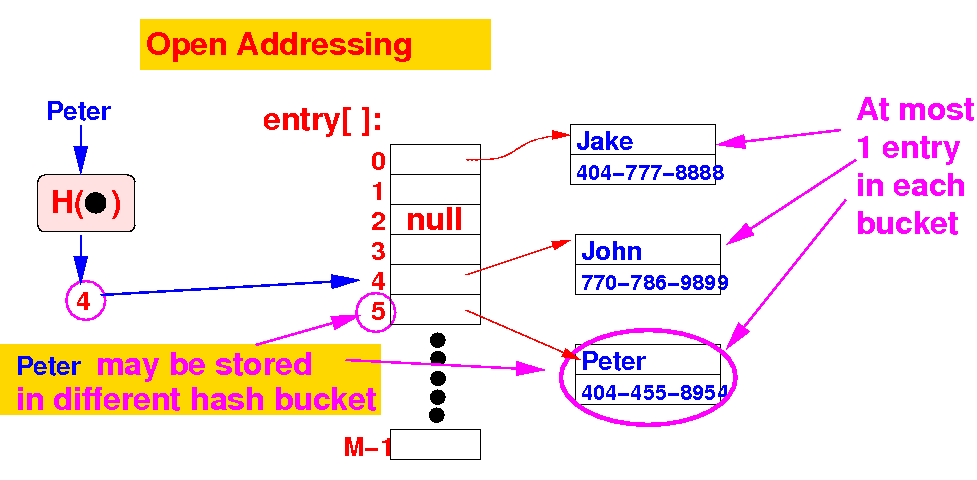
Closed Addressing vs. Open Addressing

  • Entries used in Open Addressing:

    • Since in open addressing, each hash bucket will store at most one hash table entry:

      • The entries stored In Open Addressing do not has a link variable

  • Entries used in open addressing:   no linking field

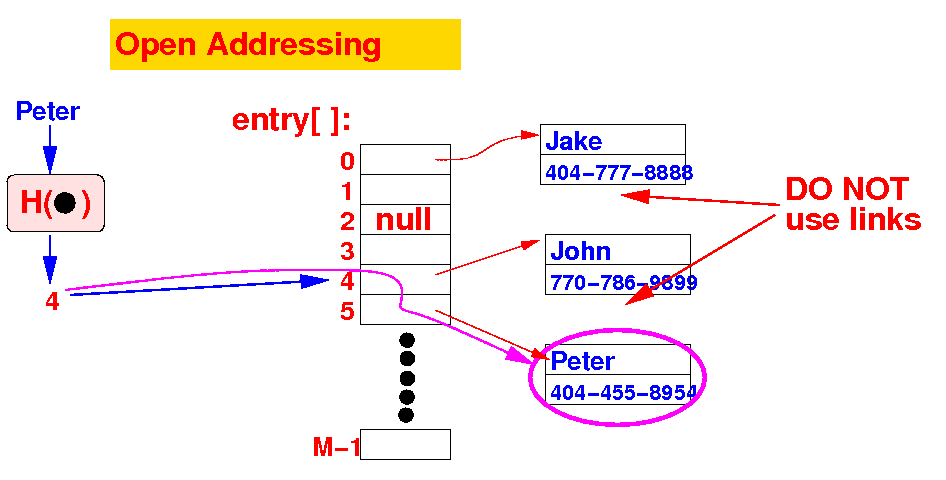
The Entry class for a hash table using Open Addressing

  • We can used the original Entry<K,V> class (which was used in the ArrayMap<K,V>) in the Open Addressing technique: 

    public class Entry<K,V>
{
    private K key;     // Key
    private V value;   // Value


    public Entry(K k, V v)  // Constructor
    {
        key = k;
        value = v;
    }

    ... // Methods omitted for brevity
}

  • We have used this Entry<sK,V> class to implement the ArrayMap dictionary data structure

  • The same Entry object can be used in Open Addressing

Collision resolution in Open Addressing

  • Suppose 2 different keys (John and Peter) hash into the same hash bucket (e.g.: 4)

  • The first key (e.g.: John) is inserted in the hash bucket (4):

    Now the hash bucket 4 is full

    (Because each hash bucket can store at most one hash table entry)

Collision resolution in Open Addressing

  • Insertion of the second key (e.g.: Peter) will find that the hash bucket (4) is full:

    The insert algorithm will start at the hash index and find the next available hash bucket that can use used to store the key

  • The procedure to find the next available hash bucket is called:

    • Rehashing
      Note:   rehashing is not random but deterministic (= computable)

Collision resolution in Open Addressing

  • Rehash algorithms used to resolve collision in Open Addressing:

    1. Linear Probing:

      • In linear probing, the hash table is searched sequentially starting from the hash index value

      In other words, the "rehash" function is: 

       rehash(key) = (h+i)%M   where  h = H(key) and i = 1, 2, ..

    2. Quadratic Probing: uses the "rehash" function: 

       rehash(key) = (h+i2)%M   where  h = H(key) and i = 1, 2, ..

    3. Double hashing: which uses the "rehash" function: 

       rehash(key) = (h+i*H2(key))%M   // H2 is a 2nd hash function