Performance Analysis of Hashing with Seperate Chaining

  • Consider a hash table using seperate chaining:

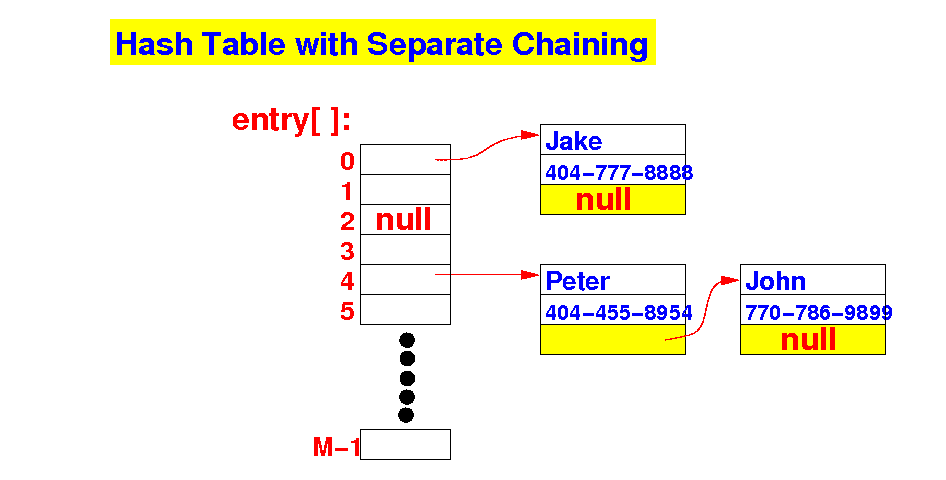
  • Due to the randomization of the hash value:

    • Some entries in the hash table has no keys (e.g.: entry[2])

    • Some entries in the hash table has exactly 1 key (e.g.: entry[0])

    • Some entries in the hash table has > 1 key (e.g.: entry[4])

Performance Analysis of Hashing with Seperate Chaining

  • Operations on a hash table always uses the hash value:

  • The hash value will select one specific hash bucket:

    • The search key will be:

      1. Found in this hash bucket                 or

      2. Not found in this hash bucket

Performance Analysis of Hashing with Seperate Chaining

  • Therefore, operations on a hash table will always examine all keys in one search bucket:

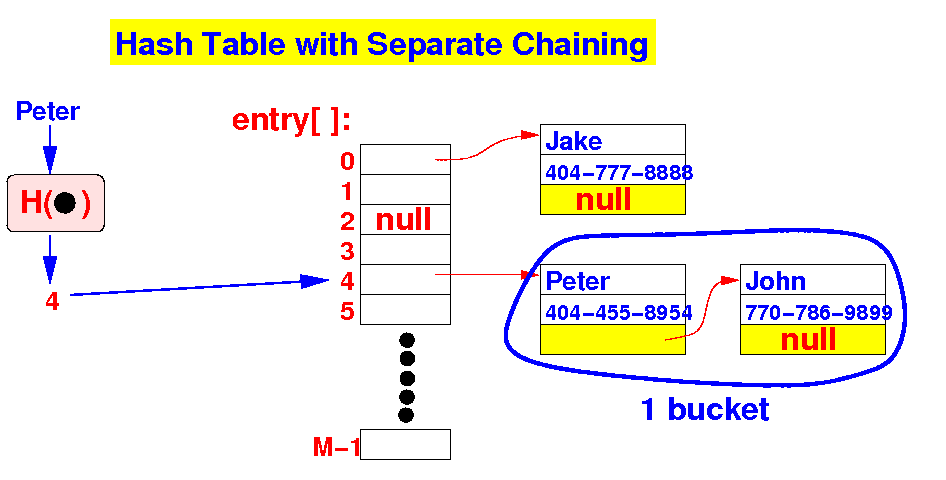
  • Therefore, the running time of operations on a hash table is equal to:

    • The number of entries stored inside one bucket in the hash table

  • Problem:   how many entries will be stored inside 1 bucket ???

Performance Analysis of Hashing with Seperate Chaining

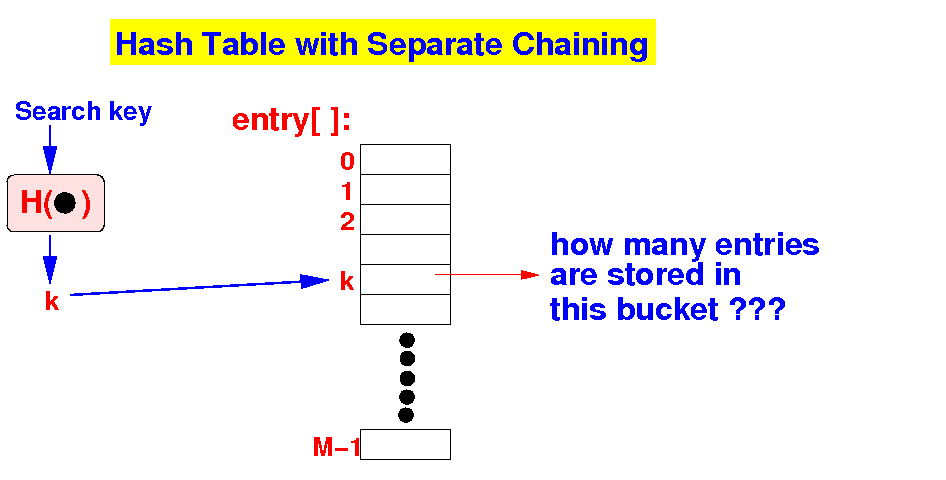
  • Problem:   how many entries will be stored inside 1 bucket ???

  • Fact:

    • A search key that has hash value k is stored in the bucket k

  • Therefore:   # entries in bucket k = # keys where H(key) = k

Performance Analysis of Hashing with Seperate Chaining

  • Estimating the # entries stored in a bucket:

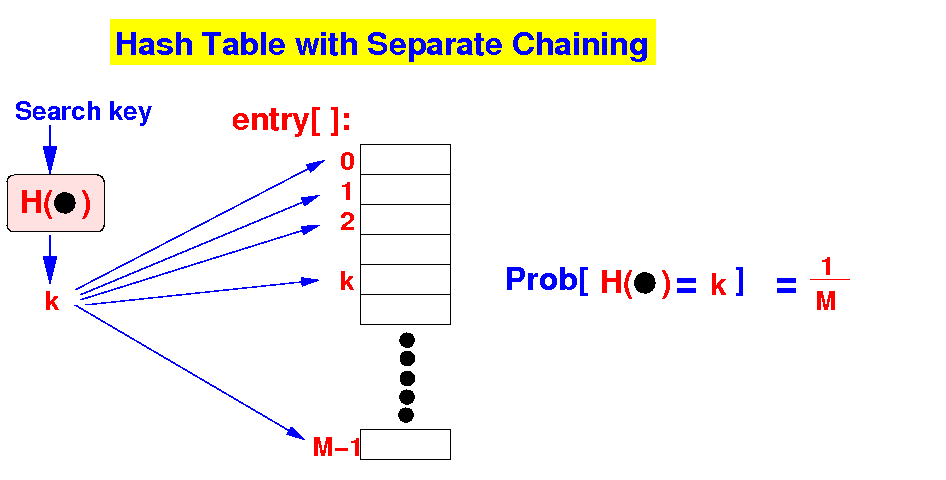
  • Assumption: uniformity

    • The ramdon hash value H(key) is uniformly distributed over the range [0..(M-1)]

      I.e.: each outcome is equally likely with probability 1/M

Performance Analysis of Hashing with Seperate Chaining

  • Suppose there are a total of n items/entries hashed and stored in the hash table:

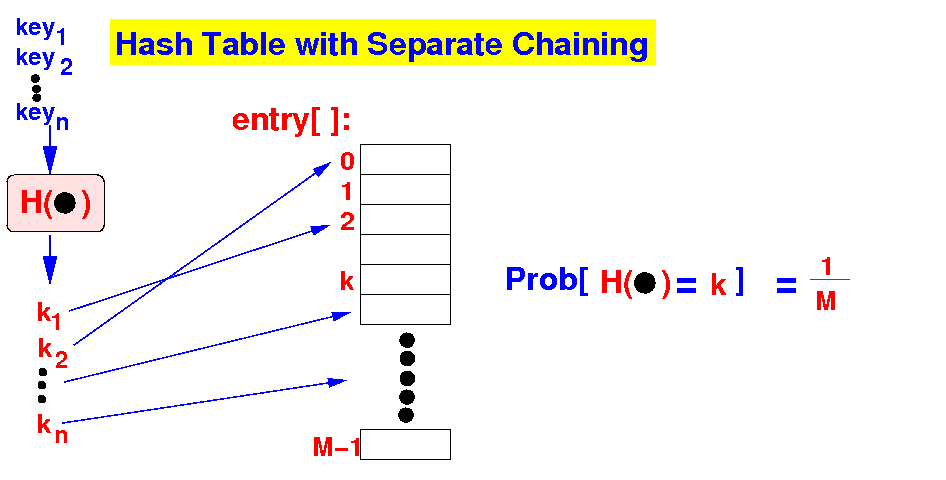
  • According to the Theory of Probability:

    • The number of items/entries in any bucket has a binomial probability distribution Bin(n, p=1/M)

  • The average number of entries in 1 bucket = n/M
    Average running time for hash operations = n/M