Useful (summation) formula in algorithm analysis

  • Commonly used formulas in algorithm analysis: 

     Triangular sums:

       1 + 2 + 3 + 4 + ... + N       = N(N+1)/2    ≈   N2/2

 Geometric sum:

       1 + 2 + 4 + 8 + ... + N (=2n)     = 2N-1        ≈ 2N

       1 + 1/2 + 1/4 + ... + 1/N (=1/2n) = 2 - 1/N     ≈ 2

 Harmonic sum:

       1 + 1/2 + 1/3 + ... + 1/N     ≈ ln(N)

 Sterling's approximation:

   log(1) + log(2) + log(3) + ... + log(N) = log(N!) ≈ Nlog(N)

Derivation of the triangular sum formula 

        S   =   1 + 2 + 3 + ... + (N-3) + (N-2) + (N-1) + N

            =  [1 + N] + [2 + (N-1)] + [3 + (N-2)] ... 
               <------------------------------------------>
                              N/2 terms

            = N/2 (N+1)

            = N(N+1)/2

Derivation of the geometric sum formula 1 

        S   =   1 + 2 + 4 + 8 + .... + N

       2S   =       2 + 4 + 8 + .... + N + 2N
  --------------------------------------------
 
   2S - S   =   2N  -  1

        S   =   2N  -  1

Derivation of the geometric sum formula 2 

         S   =   1 + 1/2 + 1/4 + 1/8 + .... + 1/N

     (1/2)S  =       1/2 + 1/4 + 1/8 + .... + 1/N + 1/(2N)
  -----------------------------------------------------------
 
 S - (1/2)S  =   1 - 1/(2N)

     (1/2)S  =   1 - 1/(2N)

          S  =   2 - 1/N

Derivation of the Harmonic sum formula 

   S   =   1 + 1/2 + 1/3 + 1/4 + .... + 1/N  ≈ log(N)

       

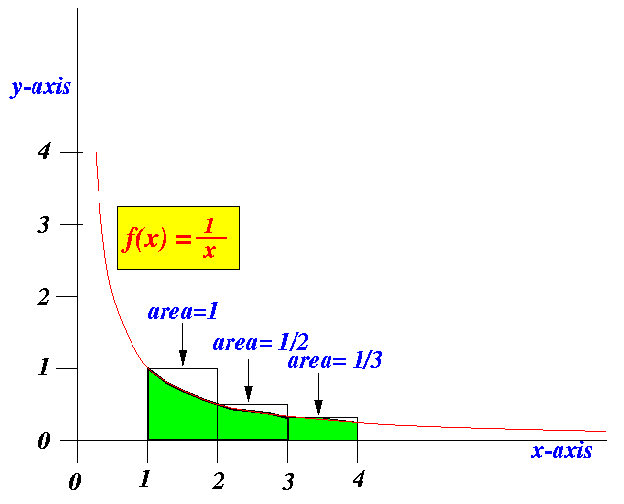  The sum of the squares = 1 + 1/2 + 1/3 + 1/4 + .... + 1/N
  The area under f(x) = log(N)