Intro to Algorithm Analysis with some simple Loop Analysis
- Consider the
following
program fragment
that process an
input array of
n elements:
double sum = 0
for ( int i = 0; i < n; i++ )
sum += array[i];
|
- How many times is the
loop body
executed ?
|
Intro to Algorithm Analysis with some simple Loop Analysis
- Consider the
following
program fragment
that process an
input array of
n elements:
double sum = 0
for ( int i = 0; i < n; i++ )
sum += array[i];
|
- How many times is the
loop body
executed ?
|
Intro to Algorithm Analysis with some simple Loop Analysis
- Consider the
following
program fragment
that process an
input array of
n elements:
double sum = 0
for ( int i = 0; i < n; i = i + 2 )
sum += array[i];
|
- How many times is the
loop body
executed ?
|
Intro to Algorithm Analysis with some simple Loop Analysis
- Consider the
following
program fragment
that process an
input array of
n elements:
double sum = 0
for ( int i = 0; i < n; i = i + 2 )
sum += array[i];
|
- How many times is the
loop body
executed ?
|
Intro to Algorithm Analysis with some simple Loop Analysis
- Consider the
following
program fragment
that process an
input array of
n elements:
double sum = 0
for ( int i = 0; i < n; i++ )
for ( int j = 0; j < n; ++ )
sum += array[i]*array[j];
|
- How many times is the
loop body
executed ?
|
Intro to Algorithm Analysis with some simple Loop Analysis
- Consider the
following
program fragment
that process an
input array of
n elements:
double sum = 0
for ( int i = 0; i < n; i++ )
for ( int j = 0; j < n; ++ )
sum += array[i]*array[j];
|
- How many times is the
loop body
executed ?
|
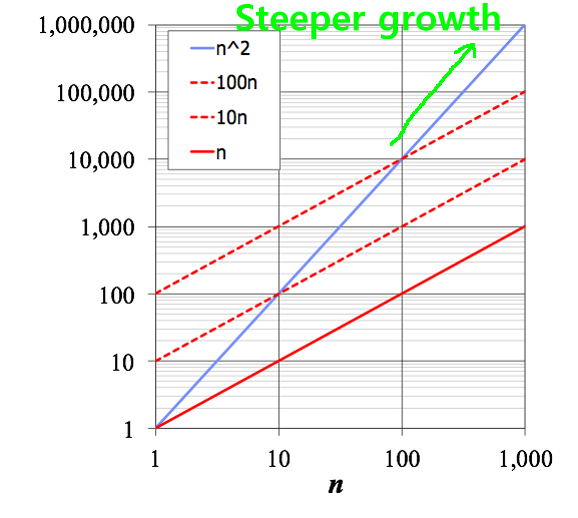
Characterizing the running time (complexity) of algorithms
- The running time of
algorithm is
a function of
the input size
- We saw in the
previous examples that the
relationship (= function)
between running time and
input size (n)
can be of these forms:
Example 1: n
Example 2: n/2
Example 3: n2
|
- The running time in terms
of input size n can be
a general
Mathematical function
E.g.:
- However, we are
mostly
interested in the:
-
"Order" of the
growth function
(and not the
exact formula)
|
|
An approximate definition
of the order of
growth
- Definition:
Given 2 function f(n) and g(n).
f(n)
f(n) ~ g(n) if ---- ---> 1 when n -> ∞
g(n)
|
- Examples:
2n + 10 ~ 2n
Try n = 100000: 2n + 10 = 200010
2n = 200000
3n3 + 20n2 + 5 ~ 3n3
Try n = 100000: 3n3 + 20n2 + 5 = 3000200000000005
3n3 = 3000000000000000
|
- In run time analysis, we can
ignore the
less significant
terms
|
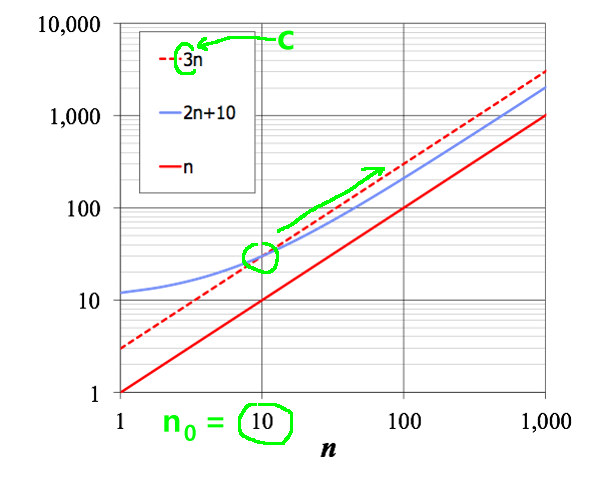
Mathematical definition of
Order of growth
- Definition:
- We call O(g(n))
- So a function
f(n) is
Big-Oh of
g(n) if:
- f(n) ≤ cg(n)
(i.e.
"dominated"
by some multiple of g(n))
for
large values of
n
|
|
Mathematical definition of
Order of growth
Mathematical definition of
Order of growth
Summary: How to perform algorithm analysis
- Determine the
frequency
(= how often) of the
primitive operation
- Primitive operation
corresponds to a
low-level (basic)
computation
with a constant execution time
(= without a loop)
Examples:
- Evaluating an
expression,
- Assigning a value to a
variable,
- Combination of the
above operations
|
|
- Characterize
it as a function
of the input size (N)
- Retain
only the
fastest growing
factor
|
- Consider the worst case behavior
and if possible, the
average behavior
|
Summary: how to obtain the
Big Oh notation
- Derive
the cost function
f(n) of your
algorithm
- Throw away
all
lower-order terms
[tilde notation]
- Drop the
constant factor
[Big-Oh notation]
|
❮
❯