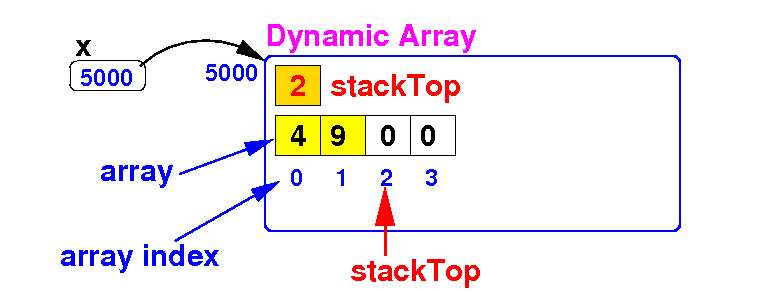
Implementing the stack with a dynamic array

  • The stack can be implemented using a dynamic array:

    1. A (fixed size) array

    2. The stackTop delineating the actual number of elements stored in the stack:

      Schematically:

  • The array is increased only when the push( ) operation encounters a full array

  • The array is reduced when the occupancy drops below a certain threshold

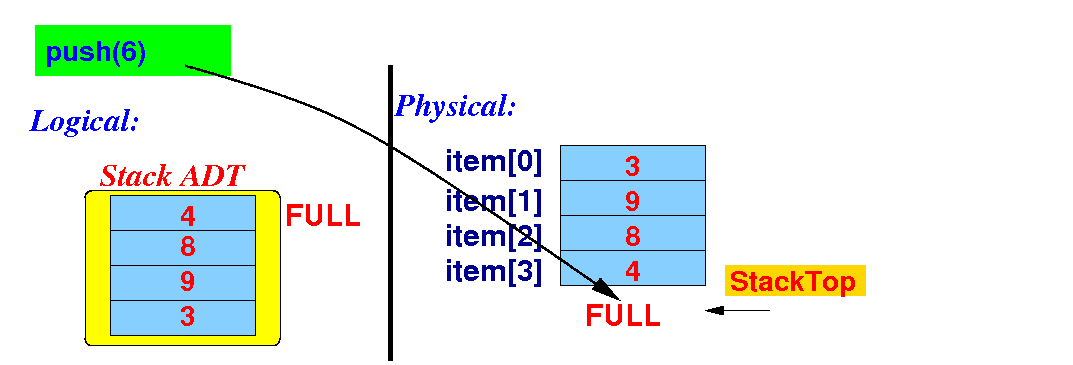
The original implementation of the push( ) method

  • Recall: the implementaion of the push( ) method for a fixed size array:                                                  

           public void push(Integer e) 
       {
          if ( isFull () )  // Change what to do when FULL
          {
              System.out.println("Full");
              return ;
          }

          item[ stackTop ] = e;    // (1) store item
          stackTop++;              // (2) increment stackTop
       }

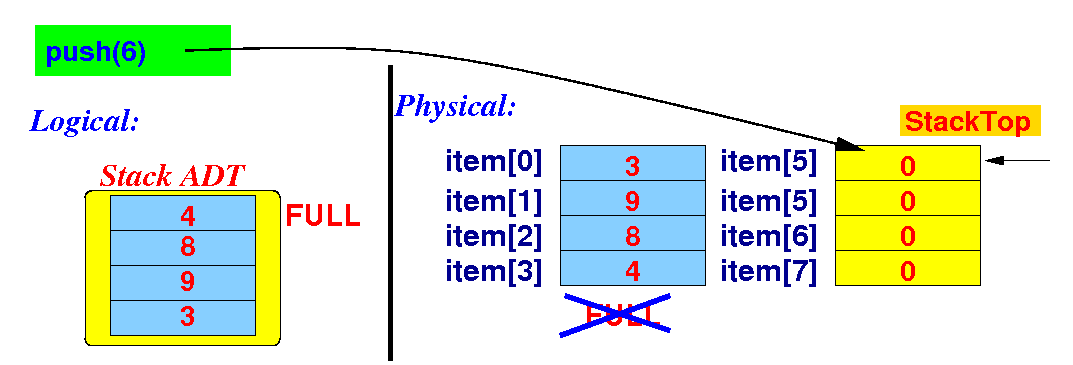
The implementation of the push( ) method for a dynamic stack

  • When the array is full, the push() method will double the array size and then push the new element: 

           public void push(Integer e) 
       {
          if ( isFull () )  // Change what to do when FULL
          {
              // Double the array size
              return ;  // Do NOT return, but continue !
          }

          item[ stackTop ] = e;    // (1) store item
          stackTop++;              // (2) increment stackTop
       }

The implementation of the push( ) method for a dynamic stack

  • The push( ) algorithm for a dynamic stack: 

           public void push(Integer e) 
       {
          if ( isFull () )  
          {
              // Double the array size
       
              Integer[] temp = new int[ 2*item.length ];

	      for ( int i = 0; i < item.length; i++ )
	          temp[i] = item[i];

              item = temp;
          }

          item[ stackTop ] = e;    // (1) store item
          stackTop++;              // (2) increment stackTop
       }

     

The implementation of the push( ) method for a dynamic stack

  • The push( ) algorithm for a dynamic stack: 

           public void push(Integer e) 
       {
          if ( isFull () )  
          {
              // Double the array size
   
              Integer[] temp = new int[ 2*item.length ];
    
	      for ( int i = 0; i < item.length; i++ )
	          temp[i] = item[i];

              item = temp;
          }

          item[ stackTop ] = e;    // (1) store item
          stackTop++;              // (2) increment stackTop
       }

    (1) create a new array that is twice the size

The implementation of the push( ) method for a dynamic stack

  • The push( ) algorithm for a dynamic stack: 

           public void push(Integer e) 
       {
          if ( isFull () )  
          {
              // Double the array size
   
              Integer[] temp = new int[ 2*item.length ];

	      for ( int i = 0; i < item.length; i++ )
	          temp[i] = item[i];
    
              item = temp;
          }

          item[ stackTop ] = e;    // (1) store item
          stackTop++;              // (2) increment stackTop
       }

    (2) copy the elements over

The implementation of the push( ) method for a dynamic stack

  • The push( ) algorithm for a dynamic stack: 

           public void push(Integer e) 
       {
          if ( isFull () )  
          {
              // Double the array size
   
              Integer[] temp = new int[ 2*item.length ];

	      for ( int i = 0; i < item.length; i++ )
	          temp[i] = item[i];
  
              item = temp;
          }

          item[ stackTop ] = e;    // (1) store item
          stackTop++;              // (2) increment stackTop
       }

    (3) make item reference to the new array

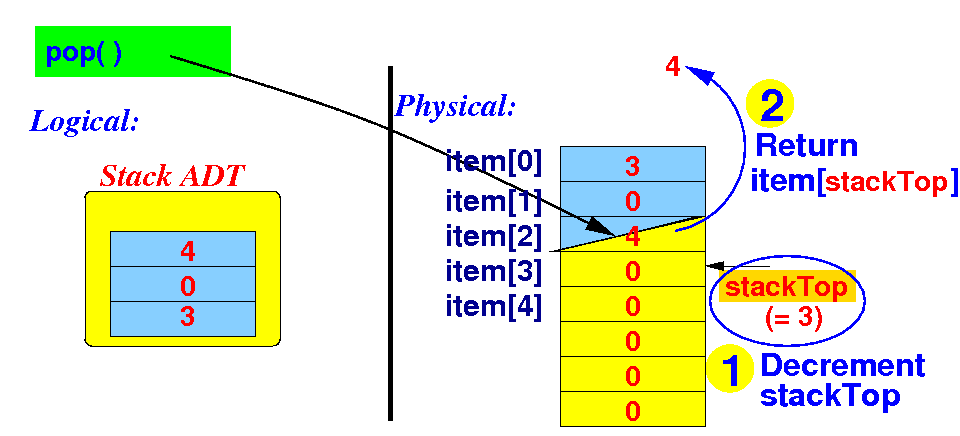
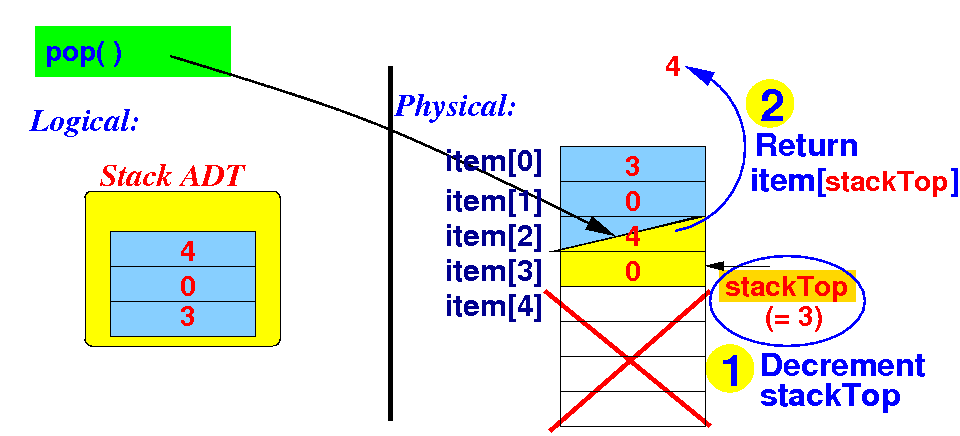
A original implementation of the pop method

  • Recall: the implementaion of the pop( ) method for a fixed size array:                                      

           public Integer pop( ) 
       {
          if ( isEmpty () )
          {
              System.out.println("Empty");
              return null;
          }

          stackTop--;              // (1) decrement stackTop
          Integer retVal = item[ stackTop ];

          return retVal;           // (2) return item
       }

A implementation of the pop method for a dynamic array

  • When the occupancy falls below some threshold, the pop() method will reduce the array size by halve: 

           public Integer pop( ) 
       {
          if ( isEmpty () )
          {
              System.out.println("Empty");
              return null;
          }

          stackTop--;              // (1) decrement stackTop
          Integer retVal = item[ stackTop ];
          if (stackTop < δ*item.length) reduce array by halve
          return retVal;           // (2) return item
       }

The implementation of the pop( ) method for a dynamic stack

  • The pop( ) algorithm for a dynamic stack: 

           public Integer pop( ) 
       {
          if ( isEmpty () )
          {
              System.out.println("Empty");
              return null;
          }

          stackTop--;              // (1) decrement stackTop
          Integer retVal = item[ stackTop ];

          // if (stackTop < δ*item.length) reduce array by halve
	  if ( statckTop < δ*item.length )
	  {
              temp = new int[ 2*item.length ];

	      for ( int i = 0; i < item.length; i++ )
	          temp[i] = item[i];
  
              item = temp;
	  }

          return retVal;           // (2) return item
       }

The implementation of the pop( ) method for a dynamic stack

  • (1) create a new array that is half the current size: 

           public Integer pop( ) 
       {
          if ( isEmpty () )
          {
              System.out.println("Empty");
              return null;
          }

          stackTop--;              // (1) decrement stackTop
          Integer retVal = item[ stackTop ];

          // if (stackTop < δ*item.length) reduce array by halve
	  if ( statckTop < δ*item.length )
	  {
              temp = new int[ item.length/2 ];

	      for ( int i = 0; i < item.length; i++ )
	          temp[i] = item[i];
  
              item = temp;
	  }

          return retVal;           // (2) return item
       }

The implementation of the pop( ) method for a dynamic stack

  • (2) copy the element to the new array: 

           public Integer pop( ) 
       {
          if ( isEmpty () )
          {
              System.out.println("Empty");
              return null;
          }

          stackTop--;              // (1) decrement stackTop
          Integer retVal = item[ stackTop ];

          // if (stackTop < δ*item.length) reduce array by halve
	  if ( statckTop < δ*item.length )
	  {
              temp = new int[ item.length/2 ];

	      for ( int i = 0; i <= stackTop; i++ )
	          temp[i] = item[i];

              item = temp;
	  }

          return retVal;           // (2) return item
       }

The implementation of the pop( ) method for a dynamic stack

  • (3) make item reference to the new array: 

           public Integer pop( ) 
       {
          if ( isEmpty () )
          {
              System.out.println("Empty");
              return null;
          }

          stackTop--;              // (1) decrement stackTop
          Integer retVal = item[ stackTop ];

          // if (stackTop < δ*item.length) reduce array by halve
	  if ( statckTop < δ*item.length )
	  {
              temp = new int[ item.length/2 ];

	      for ( int i = 0; i <= stackTop; i++ )
	          temp[i] = item[i];

              item = temp;
	  }

          return retVal;           // (2) return item
       }

The implementation of the pop( ) method for a dynamic stack

  • (4) we must only reduce array size when its size ≥ 2: 

           public Integer pop( ) 
       {
          if ( isEmpty () )
          {
              System.out.println("Empty");
              return null;
          }

          stackTop--;              // (1) decrement stackTop
          Integer retVal = item[ stackTop ];

          // if (stackTop < δ*item.length) reduce array by halve
	  if ( statckTop < δ*item.length && item.length >= 2 )
	  {
              temp = new int[ item.length/2 ];

	      for ( int i = 0; i <= stackTop; i++ )
	          temp[i] = item[i];

              item = temp;
	  }

          return retVal;           // (2) return item
       }

$64,000 question: what value do we use for δ ?

  • The value δ determines when we will reduce the size of the array by half

  • δ is a "wastage" threshold ....

    • When only the fraction of δ of the array is being used, we will reduce the wastage

  • Since we will reduce the array by half, δ must be at most 0.5: 

      Constraint:   δ  ≤  0.5

    otherwise, we will discard some valid entries in the stack !!!

  • What is a good value for δ ???

    • 0.5 ???
    • 0.25 ???
    • etc, etc

Why δ = 0.5 is a terrible choice

  • Consider this demo program: 

        public static void main(String[] args)
    {
        IntegerStack s = new IntegerStack();

        s.push(1);
        s.push(2);

        System.out.println("---- Start of push/pop sequence");
        s.push(5);    // Doubles the array
        s.pop();      // Halves the array
        s.push(5);    // and so on...
        s.pop();
        s.push(5);
        s.pop();
    }

    You will see a "jo-jo" effect in increase/descrease of the array...

  • δ = 0.25 is better !

DEMO: demo/09-stack/02-dyn-array/Demo2.java

Intro to running time analysis...

  • Consider the push( ) algorithm using a dynamic array: 

           public void push(Integer e) 
       {
          if ( isFull () )  
          {
              // Double the array size
   
              Integer[] temp = new int[ 2*item.length ];

	      for ( int i = 0; i < item.length; i++ )
	          temp[i] = item[i];   // Store
  
              item = temp;
          }

          item[ stackTop ] = e;    // Store
          stackTop++;              // (2) increment stackTop
       }

  • On average, how many "store" statements are executed for each push( ) invocation ?

Intro to running time analysis...

  • When the stack is not Full: 

           public void push(Integer e) 
       {
          if ( isFull () )  
          {
  
   
            
               Skipped  
	    
	       
  
             
          }

          item[ stackTop ] = e;    // Store
          stackTop++;              // (2) increment stackTop
       }

    The push( ) invocation will execute 1 store statement

Intro to running time analysis...

  • When the stack is Full: 

           public void push(Integer e) 
       {
          if ( isFull () )  
          {
              // Double the array size
   
              Integer[] temp = new int[ 2*item.length ];

	      for ( int i = 0; i < item.length; i++ )
	          temp[i] = item[i];   // Store
  
              item = temp;
          }

          item[ stackTop ] = e;    // Store
          stackTop++;              // (2) increment stackTop
       }

    The push( ) invocation will execute (1 + item.length) store statement

Intro to running time analysis...

  • Suppose we have execute N push( ) operations:                                                                                                                 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements 
     to double array:        1   2       4               8  ...
   
 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... K)  where K = 2??? ≤ N
    ≤            N        +        2*K        where K = 2??? ≤ N
    ≤            N        +        2*NN 

 Average # store statements for 1 push( ) invocation = (N + 2N) / N
                                                     =  1 + 2 = 3

Intro to running time analysis...

  • Each push( ) invocation will use 1 store statement to store the item pushed:                                                         

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements 
     to double array:        1   2       4               8  ...
   
 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... K)  where K = 2??? ≤ N
    ≤            N        +        2*K        where K = 2??? ≤ N
    ≤            N        +        2*NN 

 Average # store statements for 1 push( ) invocation = (N + 2N) / N
                                                     =  1 + 2 = 3

Intro to running time analysis...

  • The stack is full when the array size is equal to 2K ==> we need use 2K store statements to copy the array in the array doubling operation: 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ...
 
 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... K)  where K = 2??? ≤ N
    ≤            N        +        2*K        where K = 2??? ≤ N
    ≤            N        +        2*NN 

 Average # store statements for 1 push( ) invocation = (N + 2N) / N
                                                     =  1 + 2 = 3

Intro to running time analysis...

  • The total # of store statements used in the execution of N push( ) calls is equal to the sum of the 2 cases: 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... M ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... M)  where M ≤ N
    ≤            N        +        2*K        where K ≤ N
    ≤            N        +        2*NN 

 Average # store statements for 1 push( ) invocation = (N + 2N) / N
                                                     =  1 + 2 = 3

Intro to running time analysis...

  • 1 + 1 + ... + 1 = N
    1 + 2 + 4 + ... + M = ??? 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... M ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... M)  where M ≤ N
    =            N        +       ???            where M ≤ N
    ≤            N        +        2*NN 

 Average # store statements for 1 push( ) invocation = (N + 2N) / N
                                                     =  1 + 2 = 3

Intro to running time analysis...

  • 1 + 1 + ... + 1 = N
    1 + 2 + 4 + ... + M = ??? 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... M ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... M)  where M ≤ N
    =            N        +       ???            where M ≤ N
   
Let:    S  =  1 + 2 + 4 + ... M

Intro to running time analysis...

  • 1 + 1 + ... + 1 = N
    1 + 2 + 4 + ... + M = ??? 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... M ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... M)  where M ≤ N
    =            N        +       ???            where M ≤ N
   
Let:    S  =  1 + 2 + 4 + ... M
       2S  =  2 + 4 + 8 + ... 2M

Intro to running time analysis...

  • 1 + 1 + ... + 1 = N
    1 + 2 + 4 + ... + M = ??? 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... M ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... M)  where M ≤ N
    =            N        +       ???            where M ≤ N
   
Let:    S  =  1 + 2 + 4 + ... M
       2S  =      2 + 4 + 8 + ... 2M

Intro to running time analysis...

  • 1 + 1 + ... + 1 = N
    1 + 2 + 4 + ... + M = ??? 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... M ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... M)  where M ≤ N
    =            N        +       ???            where M ≤ N
   
Let:    S  =  1 + 2 + 4 + ... M
       2S  =      2 + 4 + 8 + ... 2M
   2S - S  =  2M - 1

Intro to running time analysis...

  • 1 + 1 + ... + 1 = N
    1 + 2 + 4 + ... + M = 2M - 1 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... M ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... M)  where M ≤ N
    =            N        +      2*M - 1         where M ≤ N
    ≤            N        +        2*NN 

 Average # store statements for 1 push( ) invocation = (N + 2N) / N
                                                     =  1 + 2 = 3

Intro to running time analysis...

  • 1 + 1 + ... + 1 = N
    1 + 2 + 4 + ... + M = 2M - 1 

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... M ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... M)  where M ≤ N
    =            N        +      2*M - 1         where M ≤ N
    ≤            N        +      2*N - 1  = 3N - 1

 Average # store statements for 1 push( ) invocation = (N + 2N) / N
                                                     =  1 + 2 = 3

Intro to running time analysis...

  • Therefore, the average number of store statements per execution of 1 push( ) is:
      

     # times exec push():        1   2   3   4   5   6   7   8  ...  N
                          ------------------------------------------
     # store statements
     to store item pushed:   1   1   1   1   1   1   1   1  ...  1

     # store statements
     to double array:        1   2       4               8  ... K ≤ N

 # Total store statements executed
 for N push( ) invocations:

          (1 + 1 + ... 1) + (1 + 2 + 4 + ... K)  where K = 2??? ≤ N
    =            N        +      2*K - 1         where K ≤ N
    ≤            N        +      2*N - 1  = 3N - 1

 Average # store statements for 1 push( ) invocation = (3N - 1) / N
                                                     ~= 3

Run time analysis will give you a precise result on the efficiency of the algorithm !