Searching Arrays

  • Searching:

      • Searching is a very common task in computer programming.

      • Many algorithms and data structures are invented to support fast searching.

  • Seaching arrays:

      • Arrays are often used to store a large amount of data

      • Searching is the process of looking for a specific element in an array

      • There are 2 search techniques for arrays: (1) linear search and (2) binary search

The search problem for an array

  • The search problem for arrays is:

    • For a given search value key, find the index of the (first) array element that contains the search value key

    • Return −1 when the key is not found in the array

  • Example: 

        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

    int i = arraySearch(myList,  4); // Returns   1
    int j = arraySearch(myList, -4); // Returns  -1
    int k = arraySearch(myList, -3); // Returns   5

The linear search algorithm for arrays

  • The linear search algorithm compares the search value key sequentially with each element in the array.

        

  • The linear search algorithm continues to do so until the key matches an element in the array or the array is exhausted without a match being found.

  • If a match is made, the linear search returns the index of the element in the array that matches the key.

  • If no match is found, the search returns -1.

  • See an animation of the linear search algorithm:

The linear search algorithm for arrays

  • The linear search algorithm compares the search value key sequentially with each element in the array.

        

  • The linear search algorithm continues to do so until the key matches an element in the array or the array is exhausted without a match being found.

  • If a match is made, the linear search returns the index of the element in the array that matches the key.

  • If no match is found, the search returns -1.

  • See an animation of the linear search algorithm:

The linear search algorithm for arrays

  • The linear search algorithm compares the search value key sequentially with each element in the array.

        

  • The linear search algorithm continues to do so until the key matches an element in the array or the array is exhausted without a match being found.

  • If a match is made, the linear search returns the index of the element in the array that matches the key.

  • If no match is found, the search returns -1.

  • See an animation of the linear search algorithm:

The linear search algorith for arrays

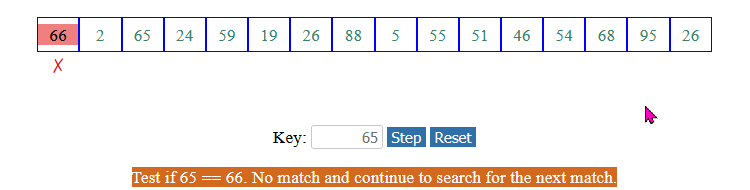
The linear search algorithm for arrays: 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

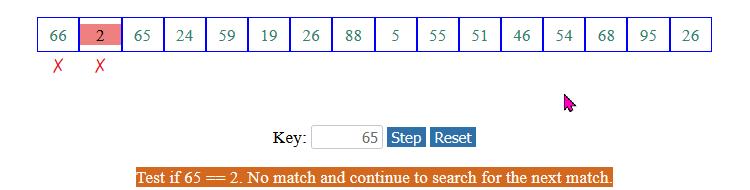
The linear search algorith for arrays

Examine each array element sequentially: 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

The linear search algorith for arrays

Look for the key value in each array element: 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

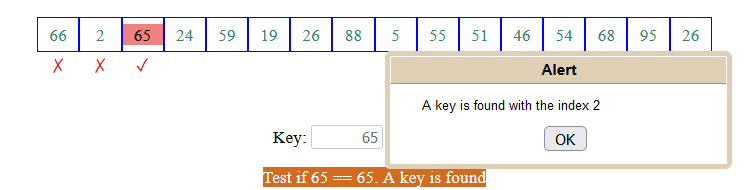
The linear search algorith for arrays

Return the index of the array element if match found: 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

The linear search algorith for arrays

When all elements have been searched, then the key is not found in the array.    We return -1. 

    /* ----------------------------------------------------
       The linear search algorithm to find key
       in the array list
       ---------------------------------------------------- */
    public static int linearSearch(int[] list, int key)
    {
        for ( int i = 0; i < list.length; i++ )
	   if ( list[i] == key )
	       return i;

        // key was not found in list[]
	return -1;
    }

    public static void main(String[] args)
    {
        int[] myList = {1, 4, 4, 2, 5, -3, 6, 2};

	int i = linearSearch(myList,  4); // Returns  1
	int j = linearSearch(myList, -4); // Returns -1
	int k = linearSearch(myList, -3); // Returns 5
    }

DEMO: demo/07-search-array/01-lin-search/Demo.java

How many steps (in terms of the input array size N) does the linear search algorithm take ?

  • Best case scenario:

    • The first element in the array contains the search key

    • Running time = 1 step (iteration)

  • Worst case scenario:

    • Array does not contain the search key

      We run through the whole array...

    • Running time = N steps (iterations)

  • Average case scenario:

    • On average, we will probe half of the array elements... (probability)

    • Running time = N/2 steps (iterations)

The binary search algorithm for arrays

  • Binary search is a more efficient (= faster) search algorithm for arrays.

  • For binary search to work, the elements in the array must already be ordered.

    • For the presentation of the binary search, we assume that the array is in ascending order.

  • The binary search compares the key with the element in the middle of the array: 

        if ( list[middle] == key )
        return middle;               // found !
    else if ( list[middle] > key )
        search in first half of array
    else
        search in secnd half of array

The binary search algorithm for arrays

  • Compare the key with the middle element in the array:

            Because 52 < 64, we continue the search in the first half of the array.

  • Notice that the middle element in the first half of the array = 42

  • See an animation of the binary search algorithm:

The binary search algorithm for arrays

  • Compare the key with the middle element in the array:

            Because 52 > 42, we continue the search in the second half of the array.

  • And so on (check out the animation)

  • See an animation of the binary search algorithm:

The binary search algorithm for arrays

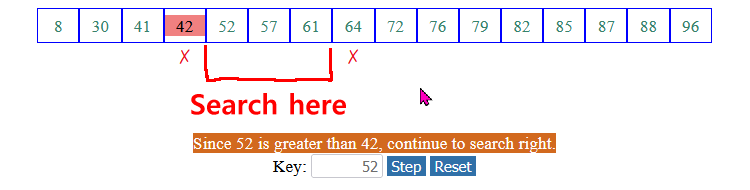
The binary search algorithm for arrays: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
               ^                                               ^
	       |					       |
	      low					      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (key < list[mid])
	        high = mid - 1;
	    else
	       low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(1) Find the middle element 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
               ^                       ^                       ^
	       |		       |		       |
	      low		      mid		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (key == list[mid])
	        return mid;
	    else if (key < list[mid])
	        high = mid - 1;
	    else
	       low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(2) If   list[mid] == key, we found the search value key: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |key|   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
               ^                       ^                       ^
	       |		       |		       |
	      low		      mid		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (list[mid] == key)
	        return mid;
	    else if (list[mid] > key)
	        high = mid - 1;
	    else
	       low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(3) If   list[mid] > key, we continue the search in the lower half of the array: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   | > |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
               ^                   ^   ^                        
	       |		   |   |		        
	      low		 high mid		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (list[mid] == key)
	        return mid;
	    else if (list[mid] > key)
	        high = mid - 1;
	    else
	       low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(4) Otherwise   ( list[mid] < key), we continue the search in the upper half of the array: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   | < |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
                                       ^   ^                   ^
	        		       |   |		       |
	      low		      mid low		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while (low <= high) 
	{
	    int mid = (low + high) / 2;

	    if (list[mid] == key)
	        return mid;
	    else if (list[mid] > key)
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(5) We must repeat the steps for the remaining array elements:    When do we stop ? 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
                                           ^                   ^
	        		           |		       |
	         		          low		      high

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (list[mid] == key)
	        return mid;
	    else if (list[mid] > key)
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(6) We stop when low > high: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
                                       ^   ^                    
	        		       |   |	<--- empty array
	         		     high low		          

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (list[mid] == key)
	        return mid;
	    else if (list[mid] > key)
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays

(7) we return -1 when key is not found: 

             +---+---+---+---+---+---+---+---+---+---+---+---+---+
    list[]:  |   |   |   |   |   |   |   |   |   |   |   |   |   |
             +---+---+---+---+---+---+---+---+---+---+---+---+---+
                                       ^   ^                    
	        		       |   |	<--- empty array
	         		     high low		          

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (list[mid] == key)
	        return mid;
	    else if (list[mid] > key)
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

The binary search algorithm for arrays   Demo program 

    public static void main(String[] args)
    {
        int[] myList = {1, 5, 9, 17, 19, 78, 99, 143, 450, 876, 999};
        int r;
        
        r = binarySearch(myList, 143);
        System.out.println("r = " + r);
    }

    public static int binarySearch(int[] list, int key) 
    {
        int low  = 0;
	int high = list.length - 1;

	while ( low <= high ) 
	{
	    int mid = (low + high) / 2;

	    if (list[mid] == key)
	        return mid;
	    else if (list[mid] > key)
	        high = mid - 1;
	    else
	        low = mid + 1;
        }

        return -1; // Not found
    }

DEMO: demo/07-search-array/02-bin-search/Demo.java

How many steps (in terms of the input array size N) does the linear search algorithm take ?

  • Best case scenario:

    • The first element in the array contains the search key

    • Running time = 1 step (iteration)

  • Worst case scenario:

    • We will study this next

  • Average case scenario:

    • Very difficult to analyze.

    • But, with we can use the worst case scenario to set an upper bound on the average case performance

Wost case analysis for the linear search algorithm

  • Worst case scenario: 

          |-------------------- input -- N elements ------------|

  • Running time = # iterations (while loop) made by the binary search algorithm

Wost case analysis for the linear search algorithm

  • Worst case scenario: 

          |-------------------- input -- N elements ------------|
iter 1|<--------------------- N/20 elements --------------->|

  • In iteration 1, there are N unprocessed elements in the input
    Testing the middle element will eliminate half of the unprocessed elements

Wost case analysis for the linear search algorithm

  • Worst case scenario: 

          |-------------------- input -- N elements ------------|
iter 1|<--------------------- N/20 elements --------------->|
iter 2                            |<-------- N/21 --------->|

  • In iteration 2, there are N/2 unprocessed elements in the input
    Testing one element will eliminate another half of the unprocessed elements

Wost case analysis for the linear search algorithm

  • Worst case scenario: 

          |-------------------- input -- N elements ------------|
iter 1|<--------------------- N/20 elements --------------->|
iter 2                            |<-------- N/21 --------->|
iter 3                                       |<----N/22---->|

  • In iteration 3, there are N/4 unprocessed elements in the input
    Testing one element will eliminate another half of the unprocessed elements

Wost case analysis for the linear search algorithm

  • Worst case scenario: 

          |-------------------- input -- N elements ------------|
iter 1|<--------------------- N/20 elements --------------->|
iter 2                            |<-------- N/21 --------->|
iter 3                                       |<----N/22---->|
iter 4                                             |<-N/23->|


       and so on...



       Algorithm stops when
                 low == high
       with 1  element left

  • In iteration 4, there are N/8 unprocessed elements in the input
    Testing one element will eliminate another half of the unprocessed elements

Wost case analysis for the linear search algorithm

  • Worst case scenario: 

          |-------------------- input -- N elements ------------|
iter 1|<--------------------- N/20 elements --------------->|
iter 2                            |<-------- N/21 --------->|
iter 3                                       |<----N/22---->|
iter 4                                             |<-N/23->|
...
iter k                                                    |-|
                                             N/2k-1 = 1 element

  • Suppose the binary search takes k iterations to complete
    Then:   N/(2k) = 1 (i.e.: after halving N elements for k times, we get 1)

Wost case analysis for the linear search algorithm

  • Worst case scenario: 

          |-------------------- input -- N elements ------------|
iter 1|<--------------------- N/20 elements --------------->|
iter 2                            |<-------- N/21 --------->|
iter 3                                       |<----N/22---->|
iter 4                                             |<-N/23->|
...
iter k                                                    |-|
                                             N/2k-1 = 1 element

       N/2k-1 = 1
 <==>      N  = 2k-1
 <==>  log(N) = k-1
 <==>   k - 1 = log(N)
 <==>     k   = log(N) + 1   (k = # iterations !)

 Worst case running time ~= log(N) steps

  • We can solve k with some simple Math operations and obtain the worst case running time of the binary search algorithm